从零开始的AutoEncoder

• 参考资料：
  1. 李宏毅-ML Lecture 21 - Unsupervised Learning - Auto-encoder

Auto-Encoder

在了解 VAE 之前，有必要先了解 Auto-Encoder（自编码器），AE 是后面一些通用模型的基础，它们都是解决在无监督学习领域的一些方法

什么是自编码器（Auto-encoder）？

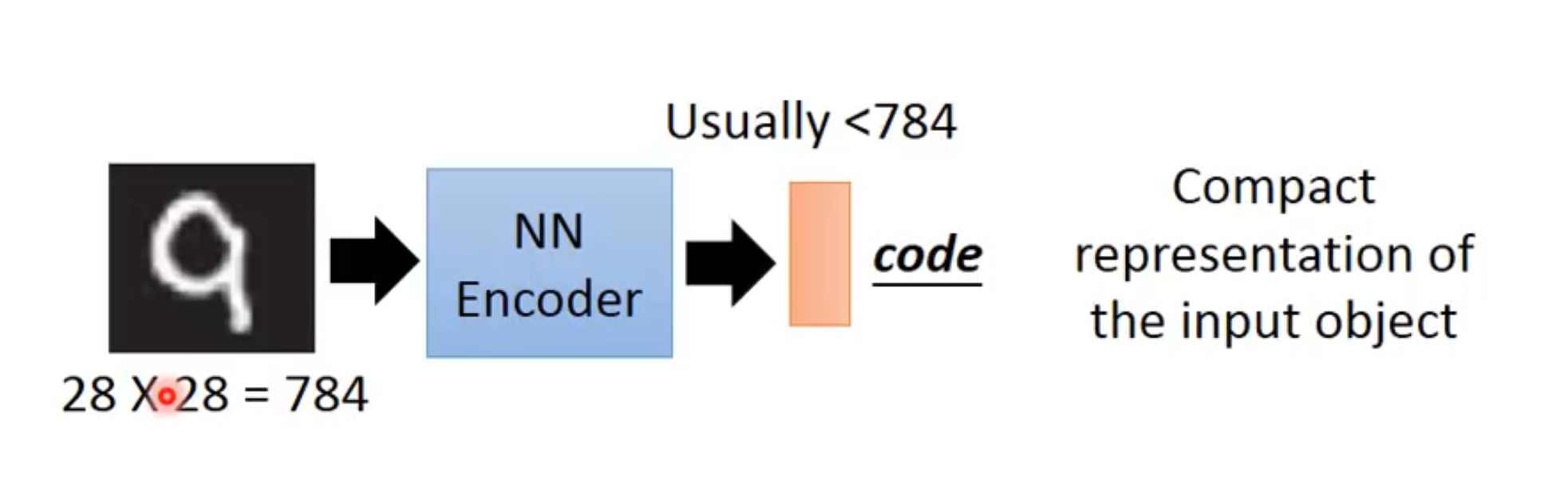
自编码器是在无监督学习领域的一个方法，对于一个输入的元素，经过编码器（可能就是一个简单全连接）后，生成了一个输出code，code的维度通常会比输入小，从而达到压缩特征的效果

但只有单一的输出是无法进行无监督学习的，因此我们引入了解码器来完成自监督的学习

输入一个 code，通过一个解码器，输出一个元素，目的是通过 code 重构出原始的输入对象

从 PCA 看自编码器

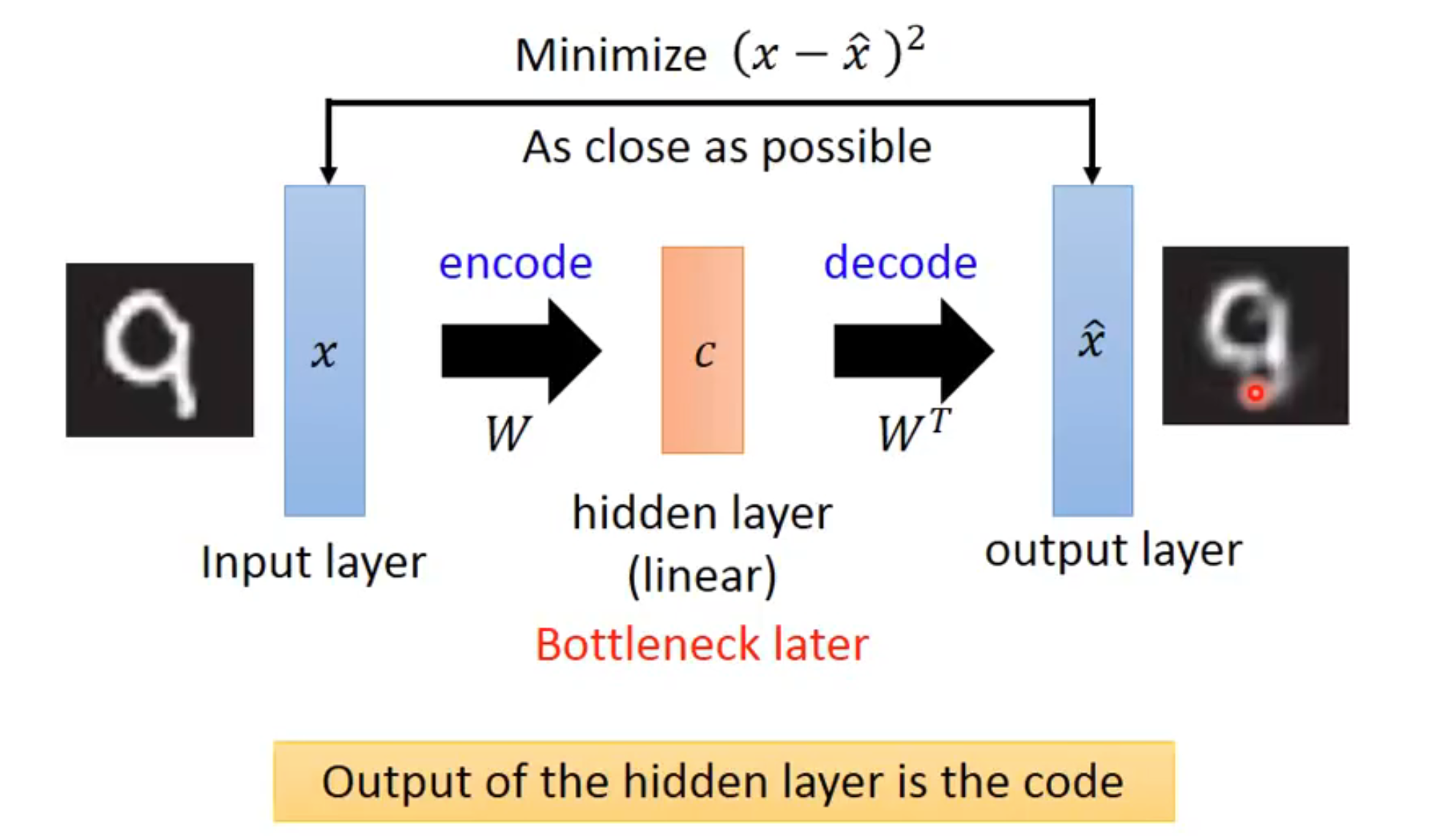
在 PCA 中，我们通过最小化输入和输出的损失，来训练中间的隐藏层（这个隐藏层也被叫做 bottleneck，因为通常隐藏层比输入小很多）

深层的自编码器

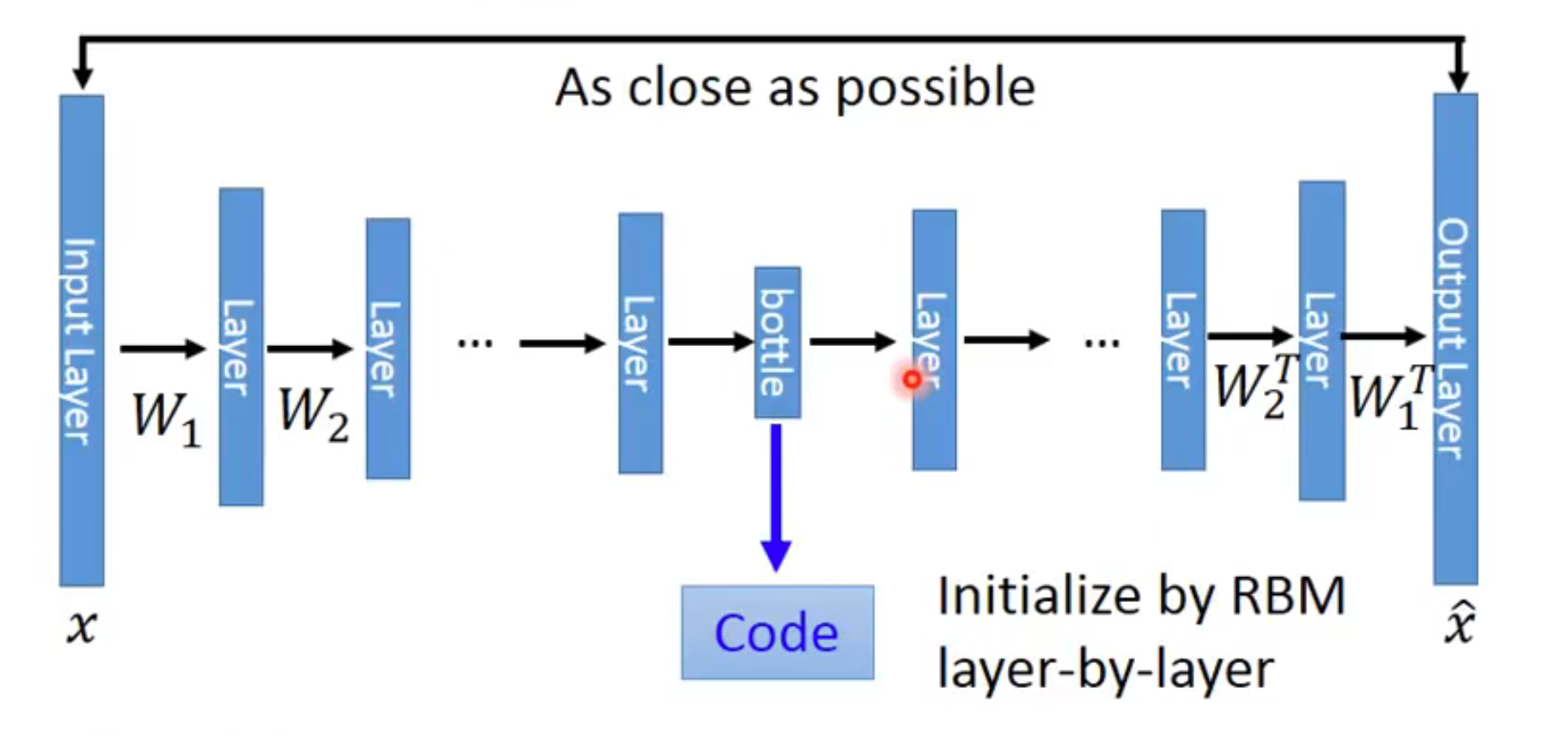
深层的自编码器和普通的神经网络没什么区别，但问题是这种方式训练效果通常不好，且必须使用RBM 进行初始化

Note

在图中encoder和decoder的layer权重是相同的，decoder多做了一次转置 在实际应用中，这不是必须的，它们也可以不是对称的

相似文本

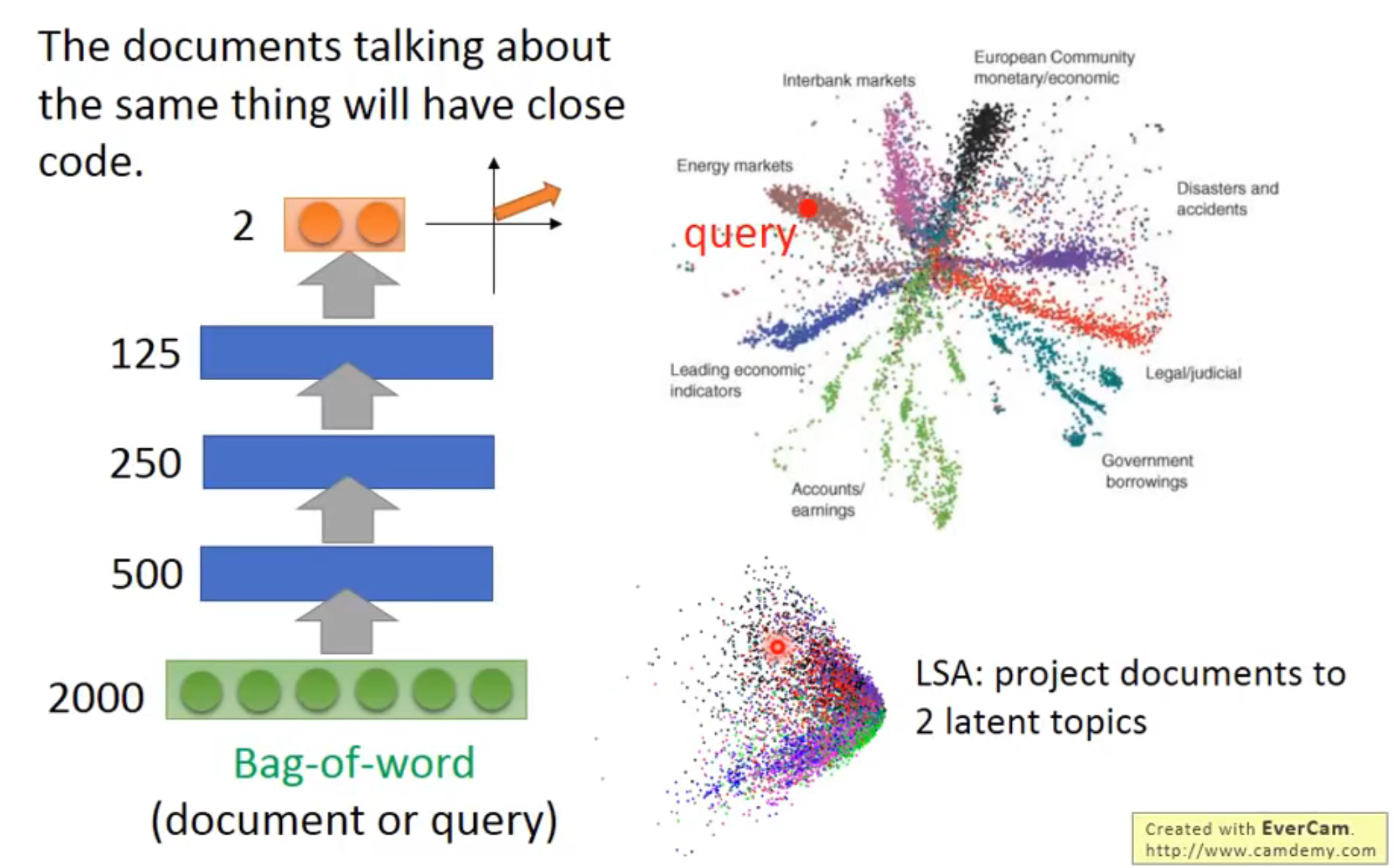
如果不使用自编码器，对所有的单词进行one-hot编码，得到的向量只能表示单词，并不能表示句子的内在关系，通过 AE 的方式，可以让网络提取出句子的关联特征，上图中code的可视化效果表明：自编码器成功将文章进行分类（通过计算code特征向量的相似度来判断是否属于同一类），能够在 2 维空间中得到较好的向量表示

相似图片

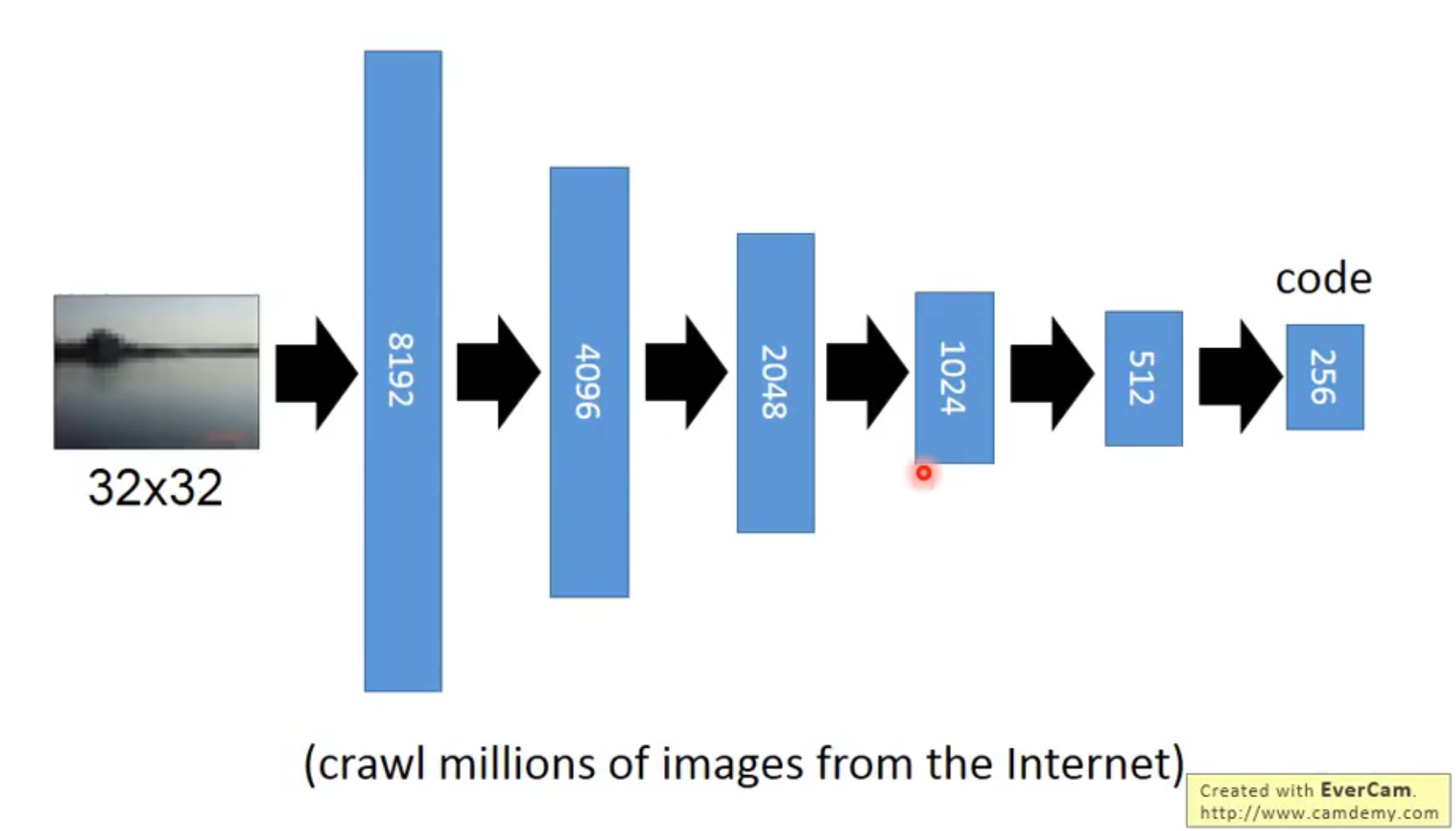
通过无监督学习，从而比较图片中的code特征向量，得到了不错的结果：

预训练

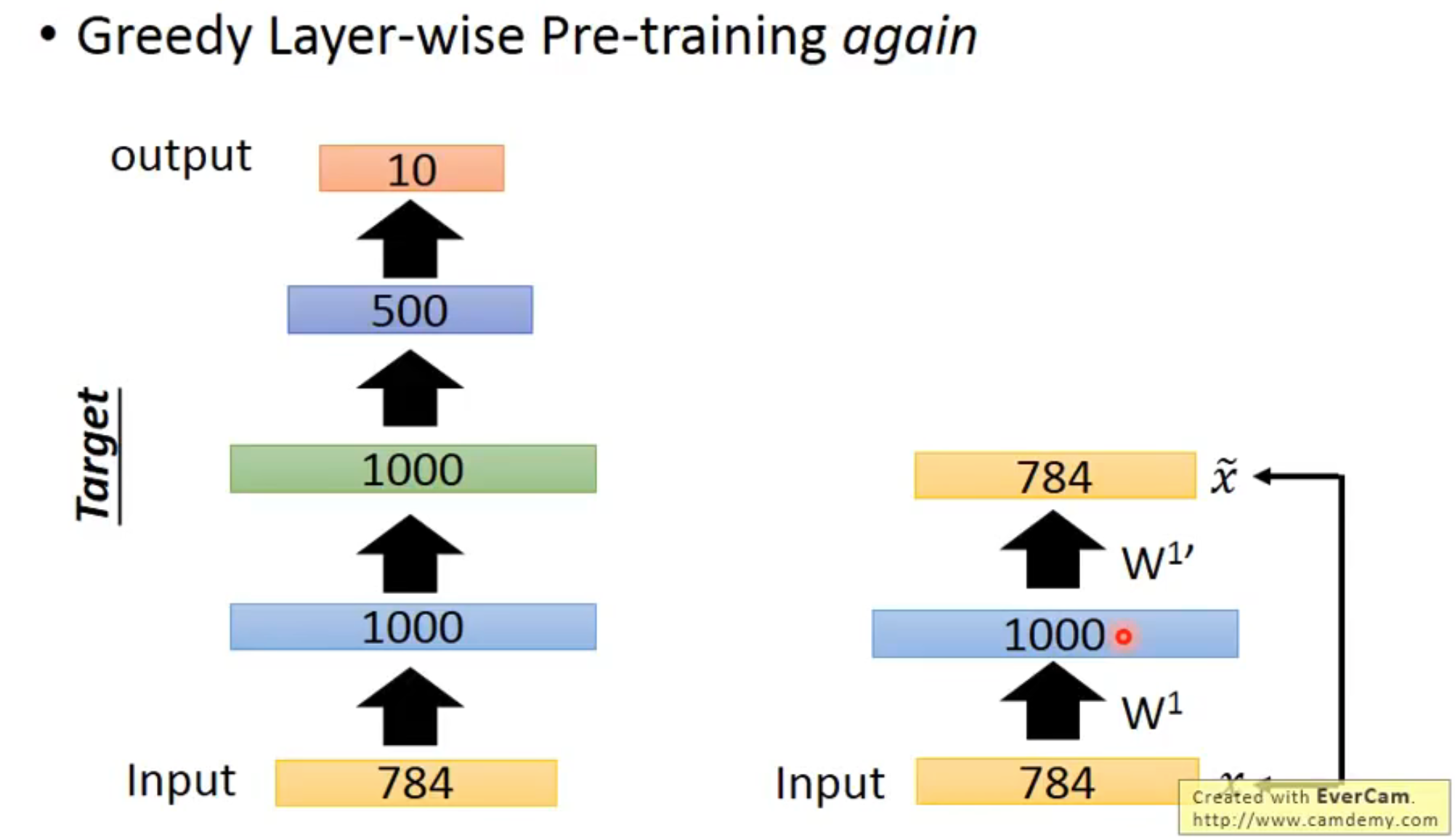
对一个网络反复使用自编码器的结构，训练中间的 code 作为该层的权重，在最后 500 和 10 的层中直接进行 random initial 进行反向传播训练

这种方法适用于标注数据较少，网络较大的情况，这时如果一个初始化权重较好的网络，可能会学到比较好的结果

Note

如果输入比 AE 中的code要小，那么需要添加一个正则化方法（通常使用$L_1$正则），防止网络直接学习一个 identical 结果

Auto-encoder 的变种

De-noising Auto-encoder

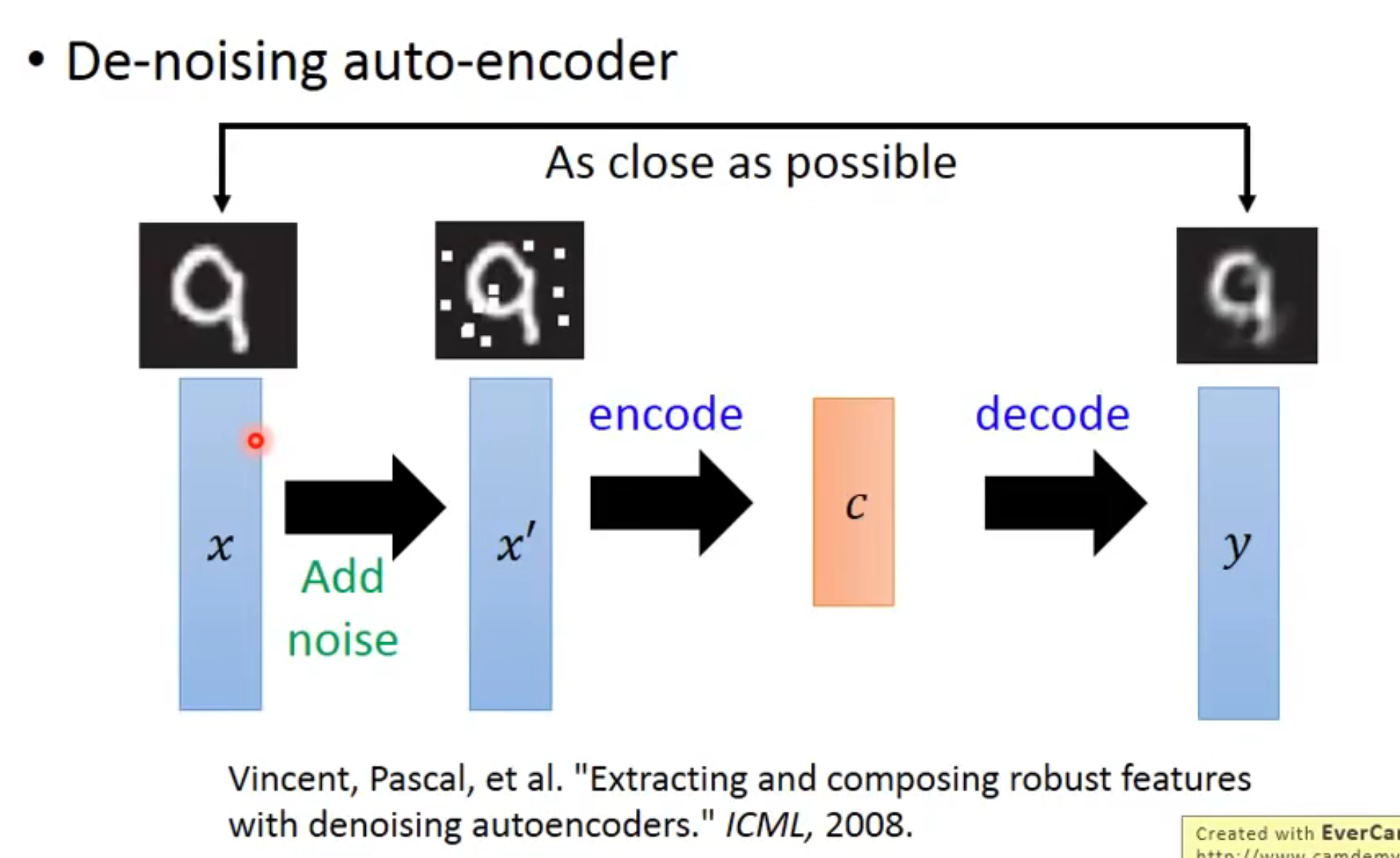
在输入前对$x$进行加噪，变成$x^{\prime }$放入网络中，最后用$x$和$y$计算损失函数，这样做可以让结果有更好的 robust

Contractive Auto-encoder

和上图一样，创新点在于添加一个 constraint，让 x‘到 code 的损失变小

Generative Models

Pixel RNN

目标：让模型生成一个图片，每次生成一个 pixel，迭代 n 次，生成一个有 n 个像素的图片

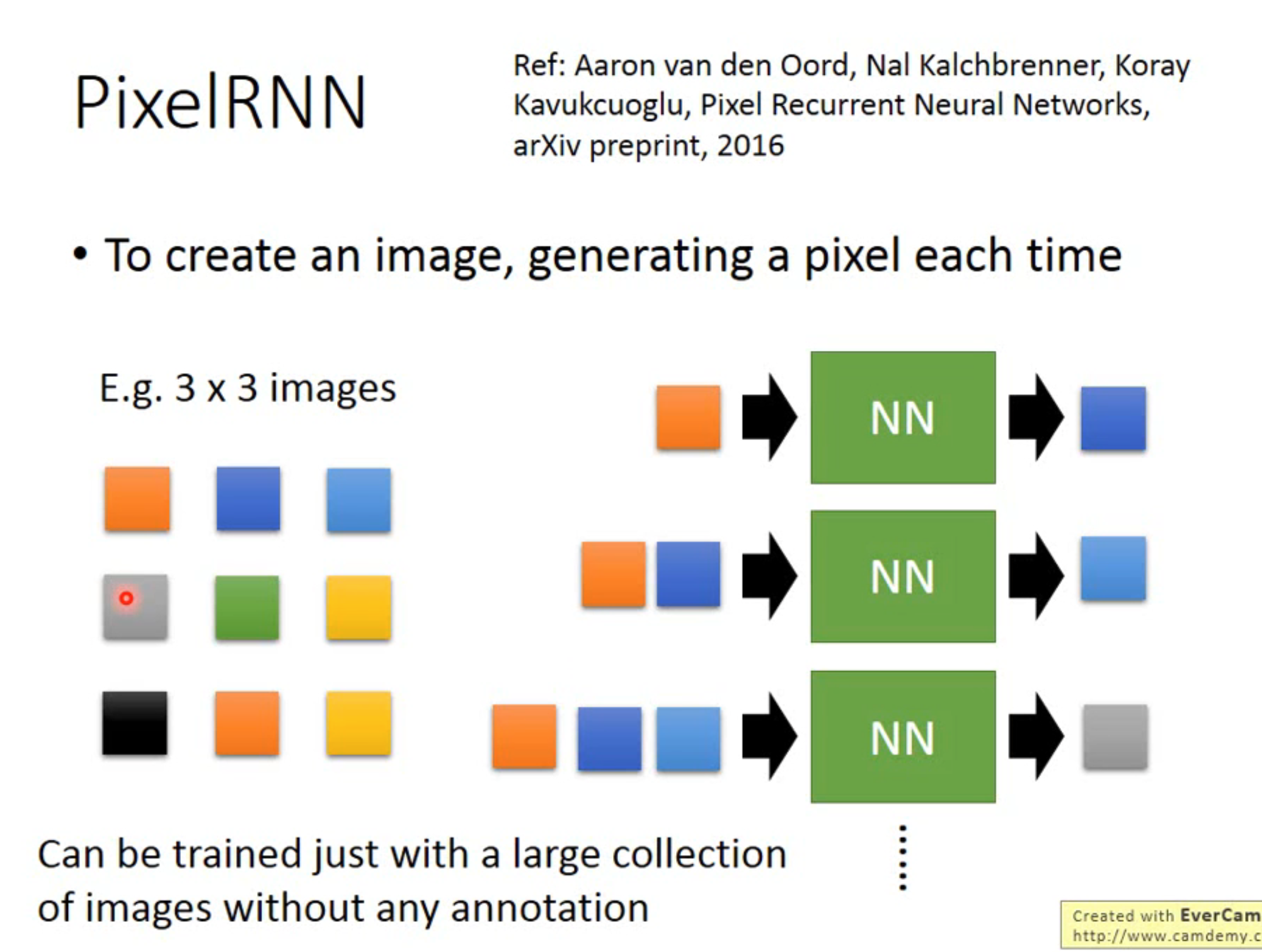
根据隐马尔可夫链假设，提取前$n-1$个 pixel 像素，去预测第$n$个像素点；好处是可以进行无监督学习，只要是图片数据，无需打标就可以使用

这种方式不仅可以应用在图像上，在声音、视频领域同样有应用：

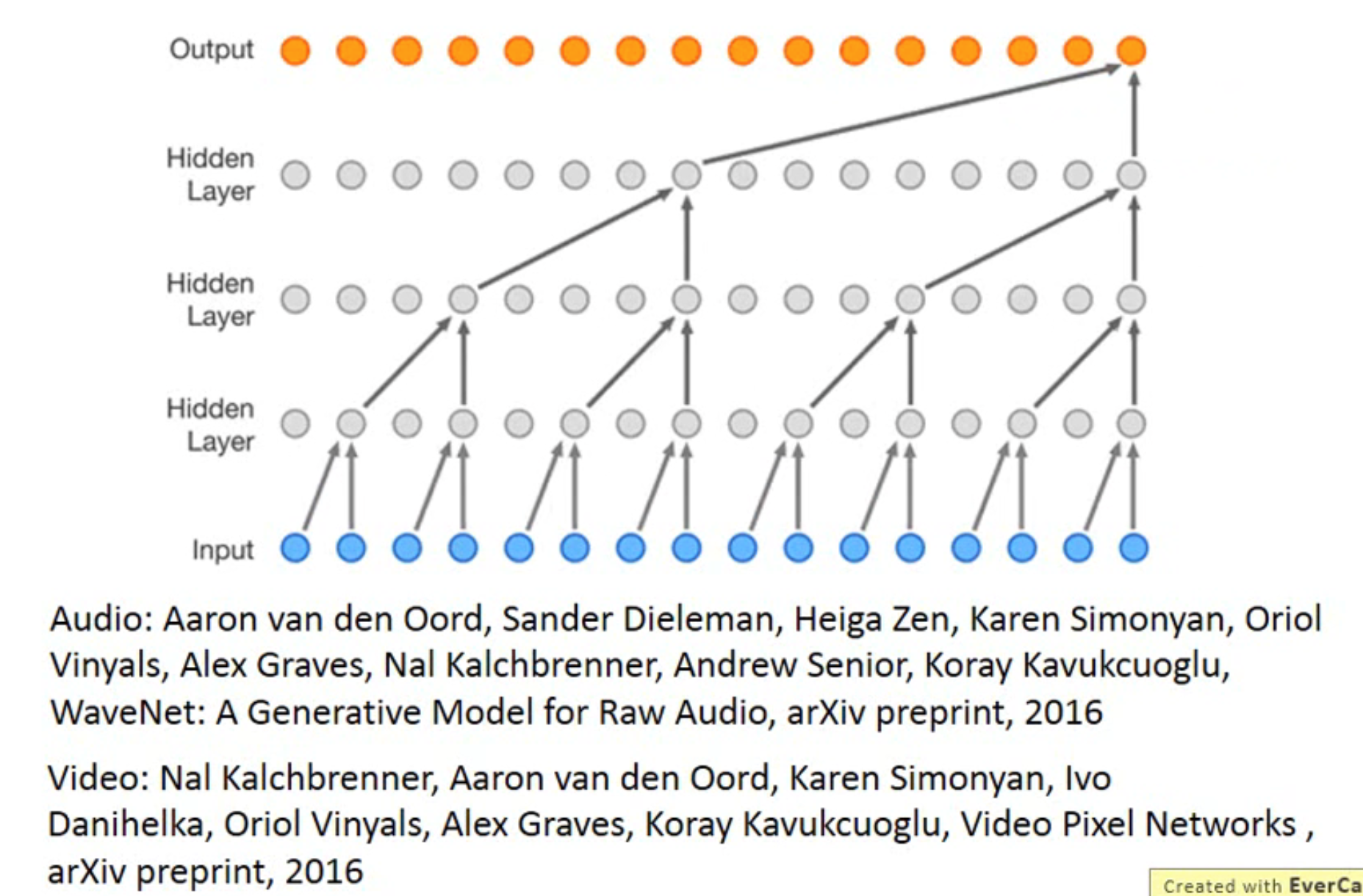
如上图所示的 WaveNet 就提供了一个新的语音生成的方式，同样是利用了隐马尔科夫链的概念，利用前一段的时间信息，预测出下一个输出

Variational Auto-encoder

参考视频

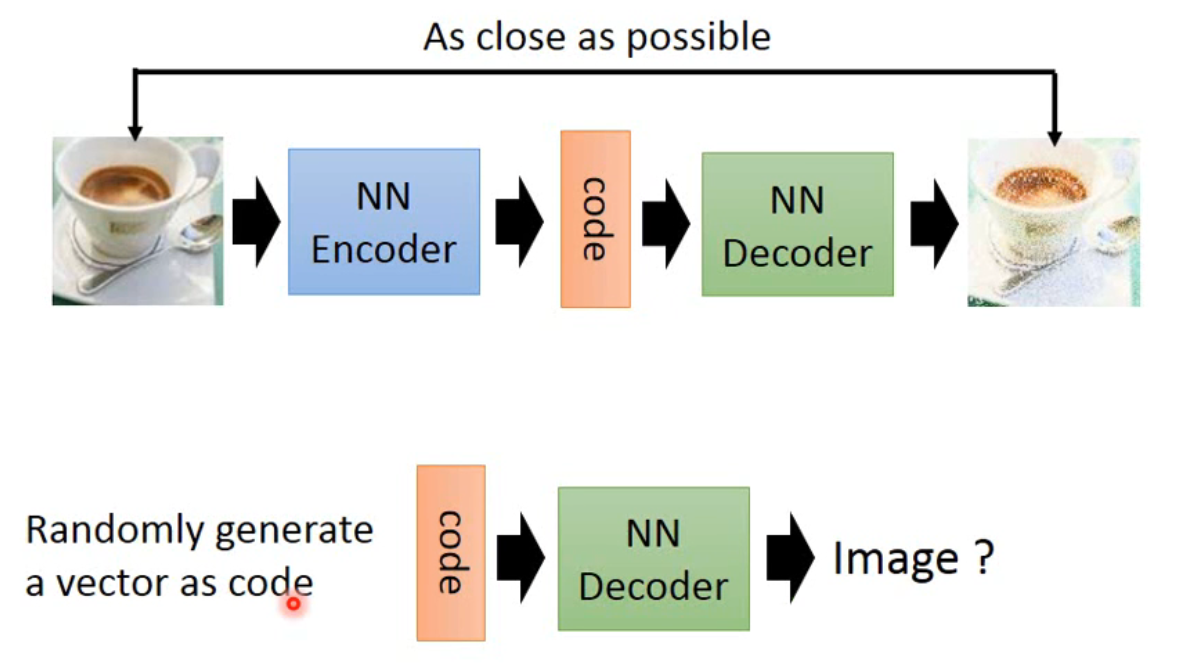
考虑 AE 的一种应用：在训练好后，我希望能使用 NN Decoder，对于一个随机生成的 code 都会 decode 出一个较好的图像，但在尝试过后发现这种方法的效果其实很差…

因此提出了 VAE 的方法，使用了若干 tricks 让结果看起来很好

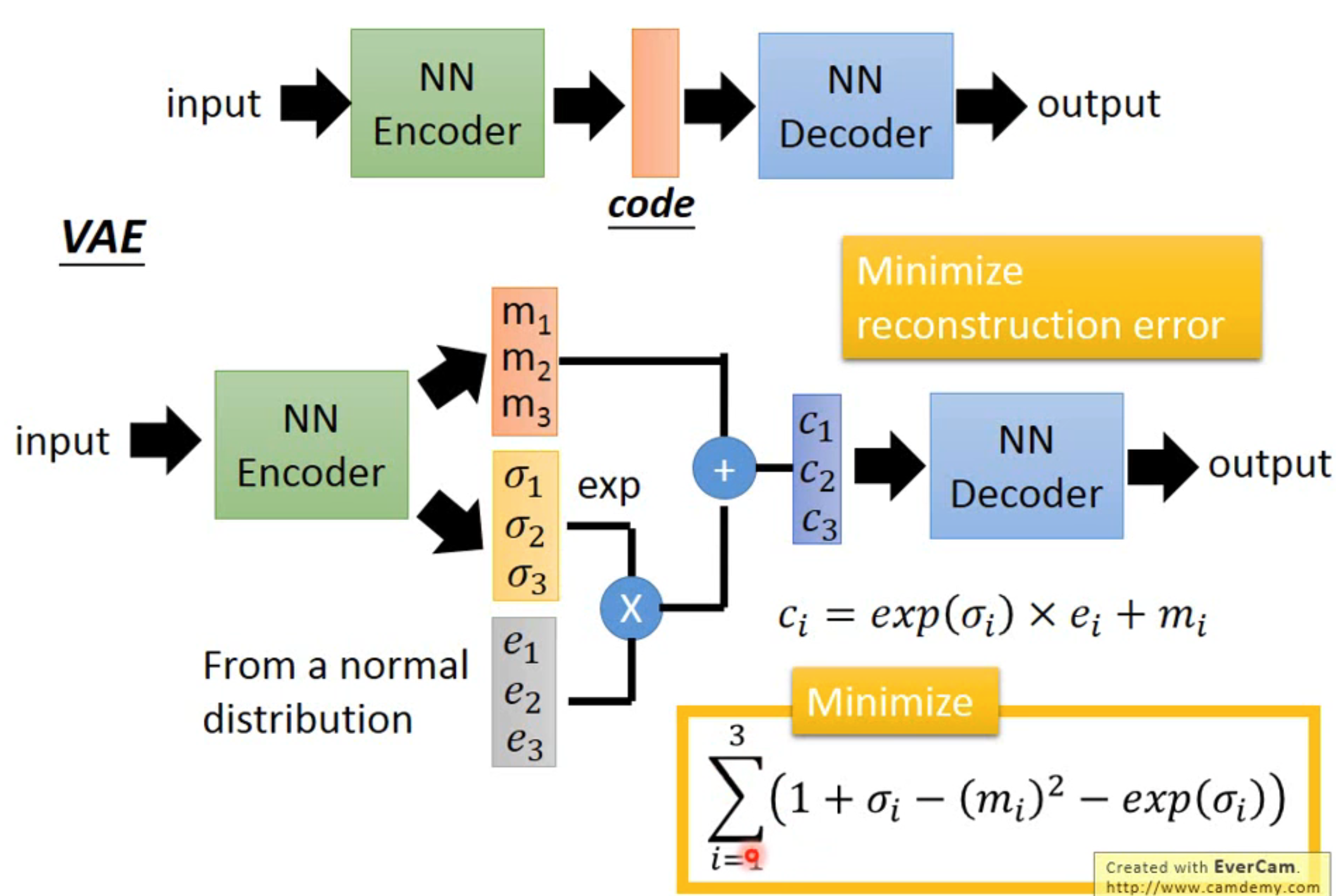
VAE 与 AE 相比，有如下不同：

1. NN Encoder 输出了三个三维的向量，分别为$m_i,{\sigma }_i,e_i$，其中$e_i$为一个正态分布
2. 对这三个输出进行相乘再相加的操作，得到$c_i$
3. loss 部分有两个
   1. 最小化重构误差，即 input 和 output 误差
   2. 最小化$\sum _{i=1}^3(1+{\sigma }_i-(m_i{)}^2-exp({\sigma }_i))$

为了能够生成可控的结果，我们需要做如下假设：

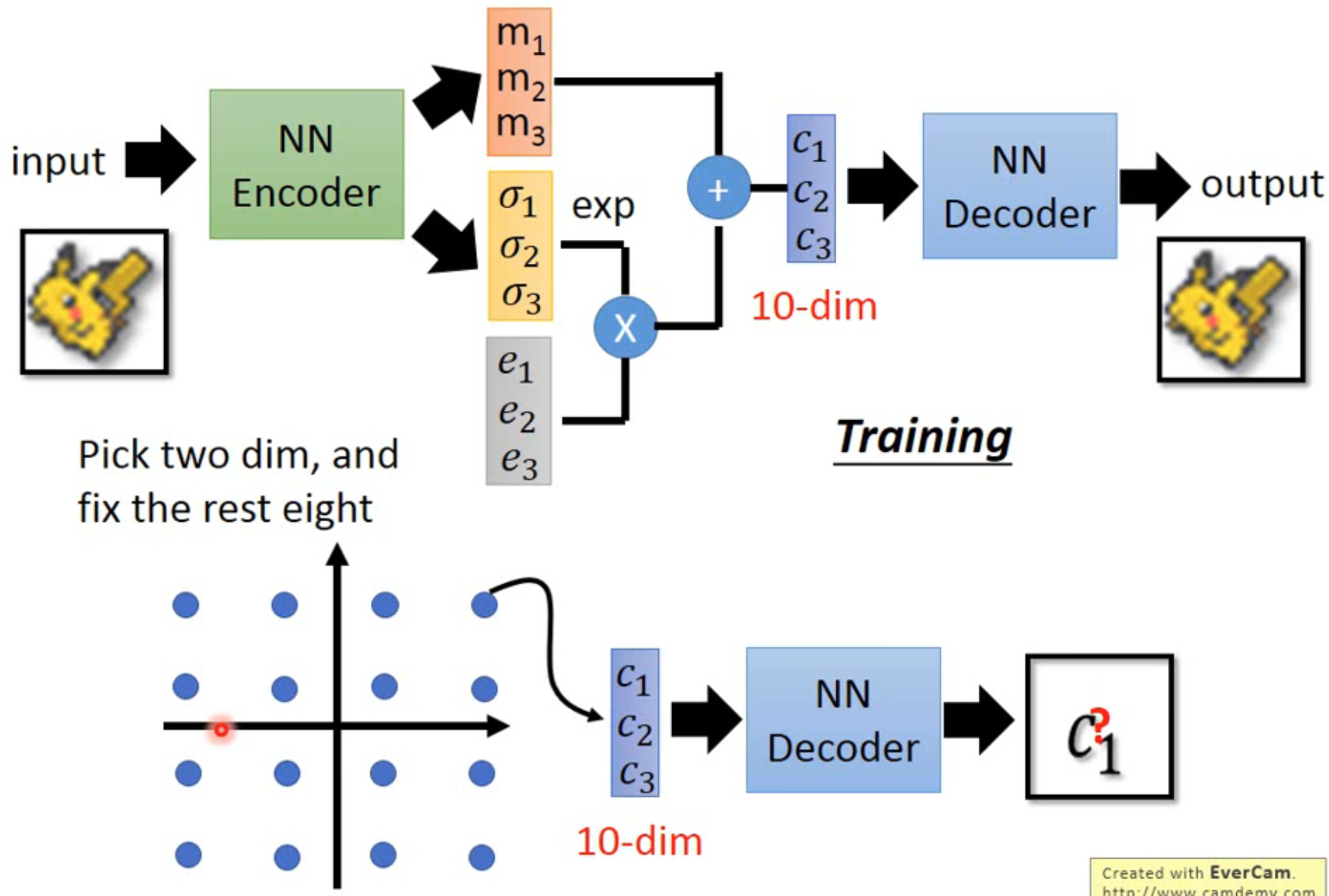
假设 code 为 10 维，那么通过定量分析，我们固定其中 8 维，选取其中 2 维并将结果进行比较，确定出这 2 维数据的变化对最后的生成结果的影响（比如这 2 维就是控制图片的亮度、对比度等等），我们希望通过这种方式控制 code 中的参数，从而控制 VAE 的生成结果

当然，也可以把模型应用在文本领域：

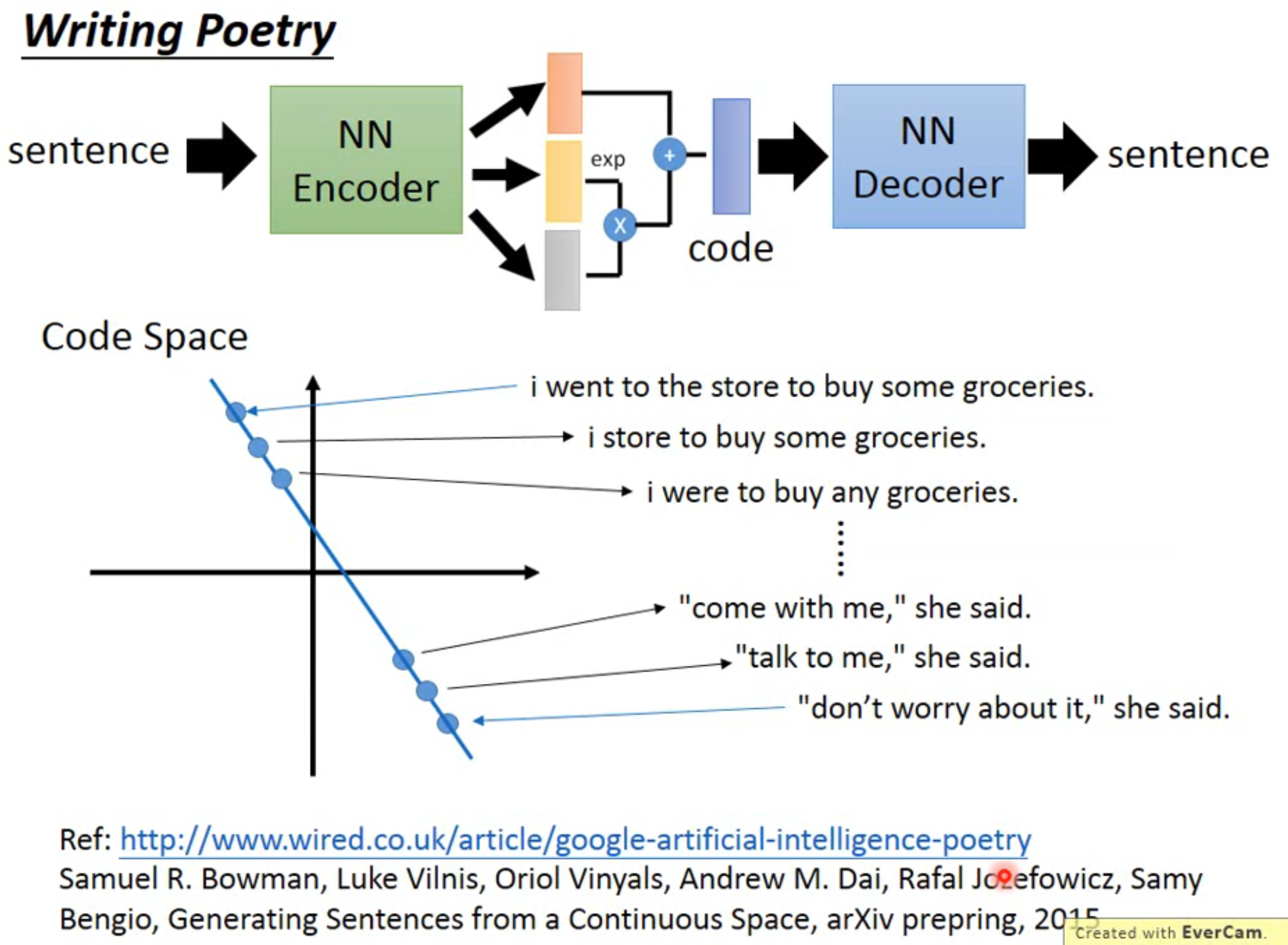
作者通过一段文本的无监督学习，得到了一个训练好的 VAE，然后对于任意两个句子，可以在code space中得到两个点，在两点的连线中可以获得一些生成的结果…（这段感觉有点像诗人根据两个句子，然后联想出诗句的过程？）

Intuitive Reason

参考视频

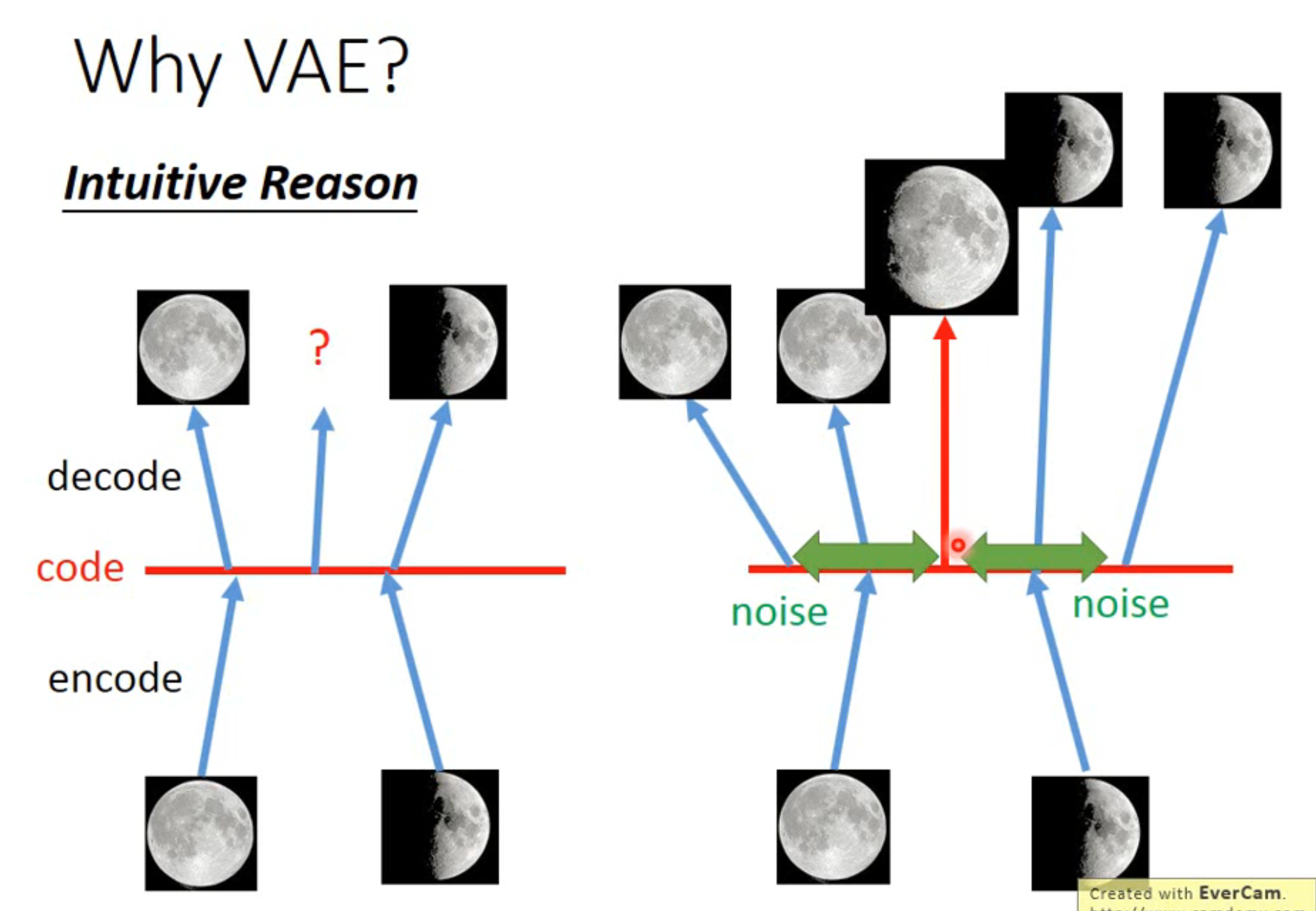
普通 Auto-Encoder 的缺点：非线性模型，导致最后的生成结果难以控制

如图中左边例子所示，input：满月图片，output：满月图片；input：半月图片，output：半月图片；如果在 code 中，取满月 code 和半月 code 的平均值并输出，我们期望能得到一个弦月图片（然而一般的 AE 很难做到这一点）

相比之下，VAE 通过在 code 层添加噪声（正态分布$e$），保证在一定范围内输出与输入一致，如图中右边例子所示，通过最小化损失函数，我们可以推断出，中间的输出既是满月又是半月，从而优化了输出结果的线性表示能力

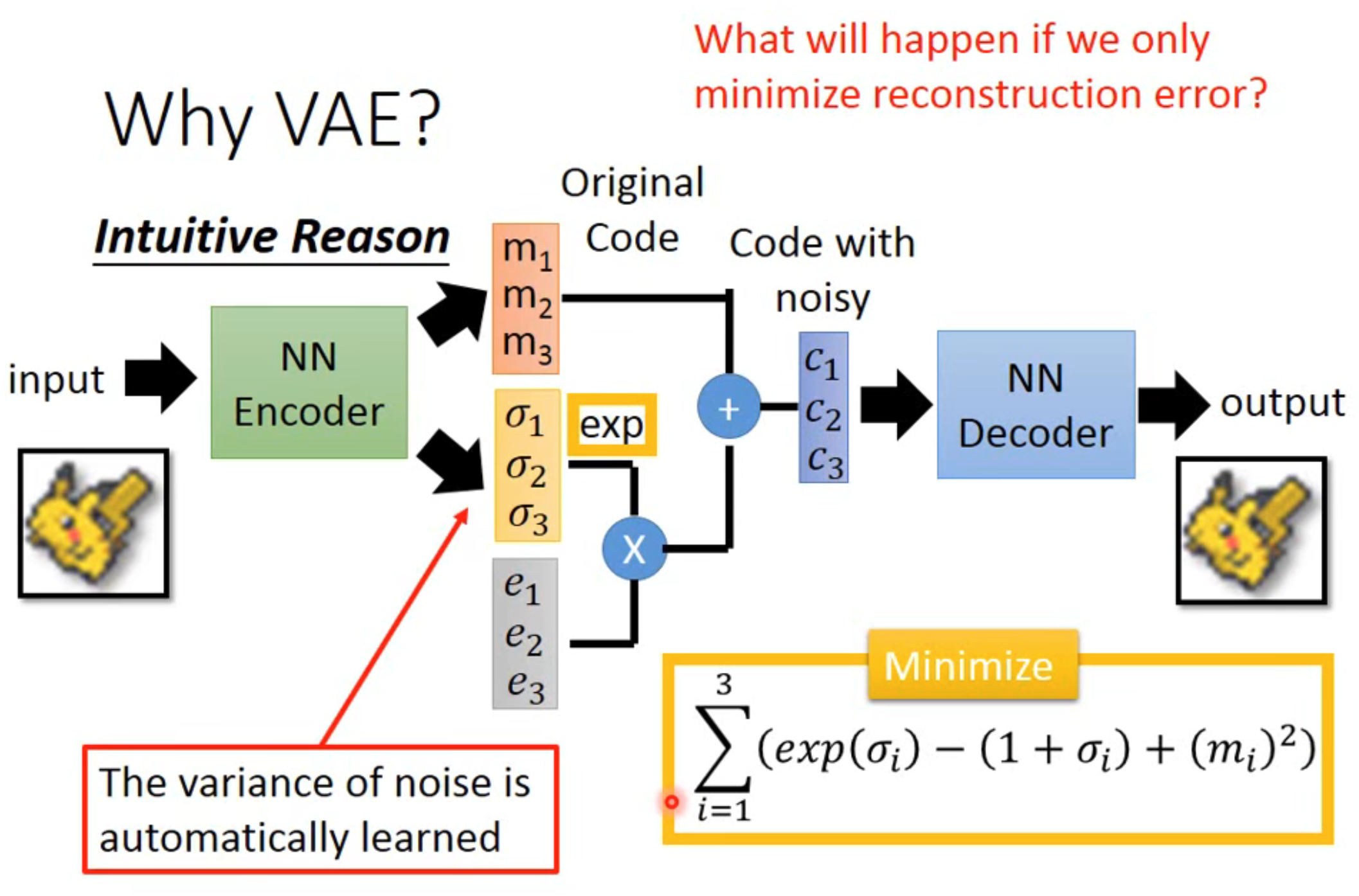
图中${\sigma }_i$学习的就是输入图片的 variance，即由模型自己学习应该添加多少噪声来保证输出最后的输出与输入一致，${\sigma }_i$取$\exp$是因为 variance 是正数

但如果仅仅只有 reconstruction error（最小化输入和输出的误差）是不够的，因为会容易得到${\sigma }_i\to -\infty$，即 variance 趋近于 0，这样网络又退化成 Auto-encoder 了

因此需要再添加一个损失函数，即$\sum _{i=1}^3(\exp ({\sigma }_i)-(1+{\sigma }_i)+(m_i{)}^2)$

前面两项$\exp ({\sigma }_i)-(1+{\sigma }_i)$在二维图像中的表示如下：

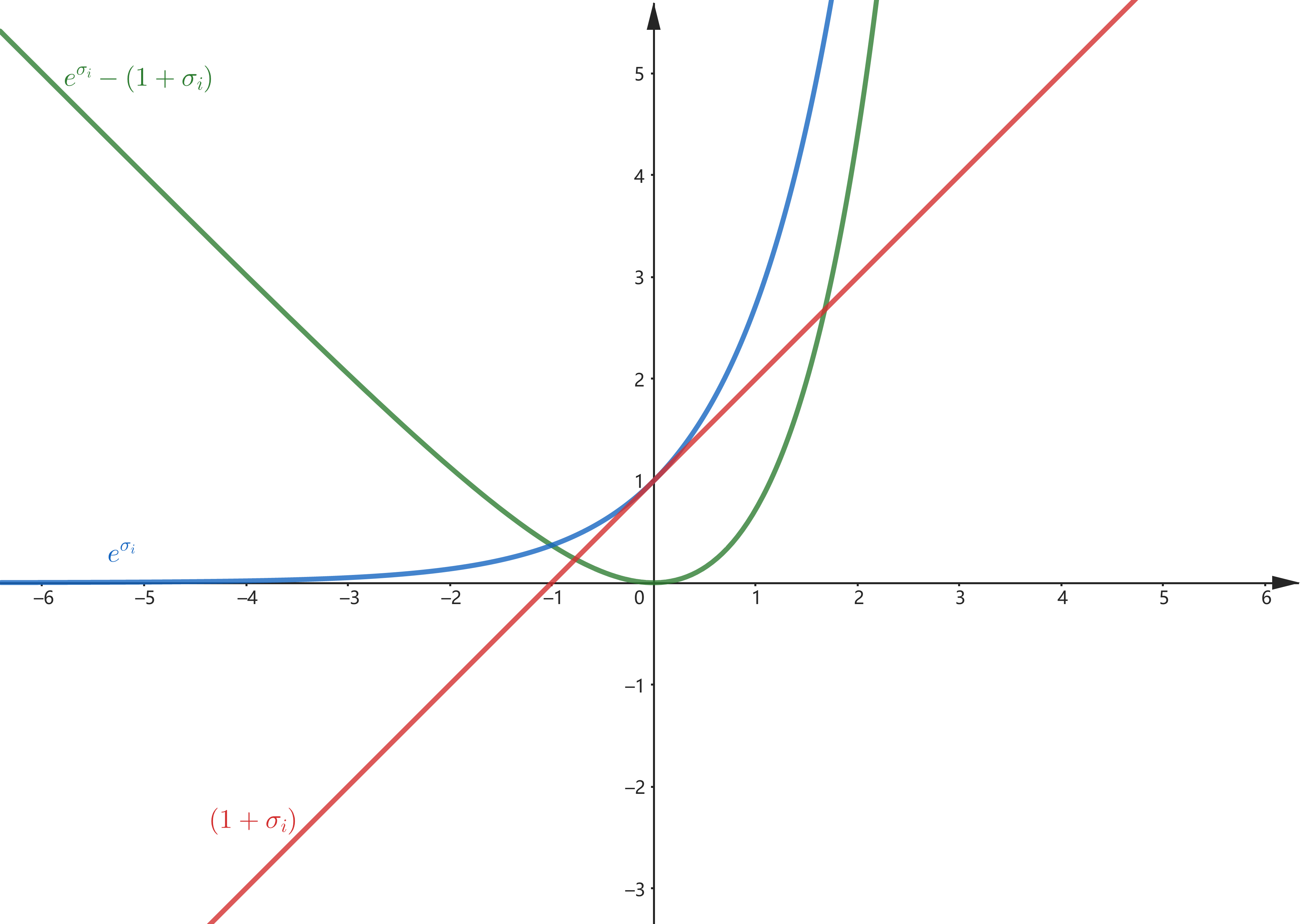
最小化损失函数的过程即 ${\sigma }_i\to 0$，这样就保证了 $variance\to 1$，从而避免了网络的“退化”

$(m_i{)}^2$则是一个正则项，防止过拟合

Mathematical derivation⭐

参考视频

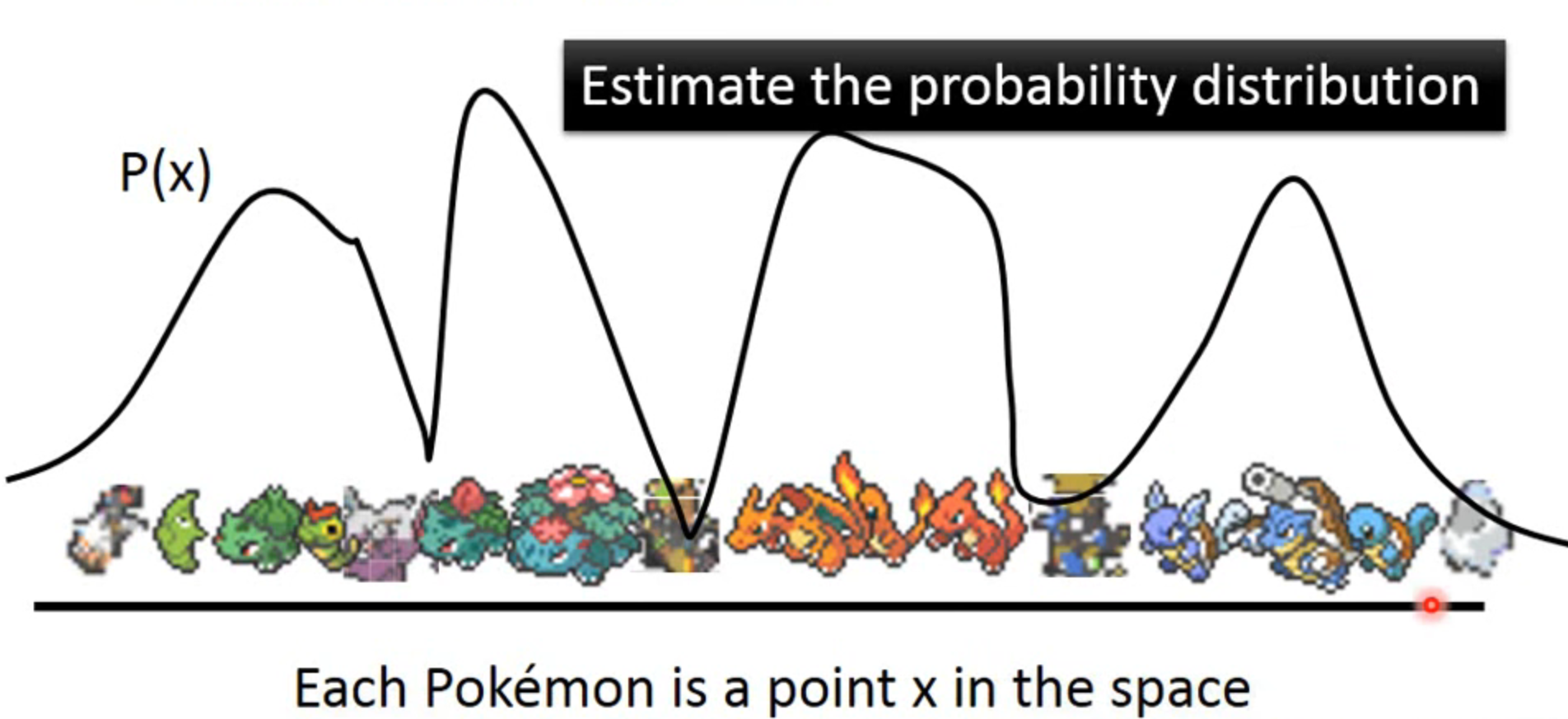
如果把每个图片看作高维空间中的一个点，那么所有的宝可梦图片在高维空间内就会呈现出一个概率分布，如果我们能够找到这个概率分布$P(x)$，就可以取概率分布高的地方作为输入，从而得到一个近似的输出

Gaussian Mixture Model

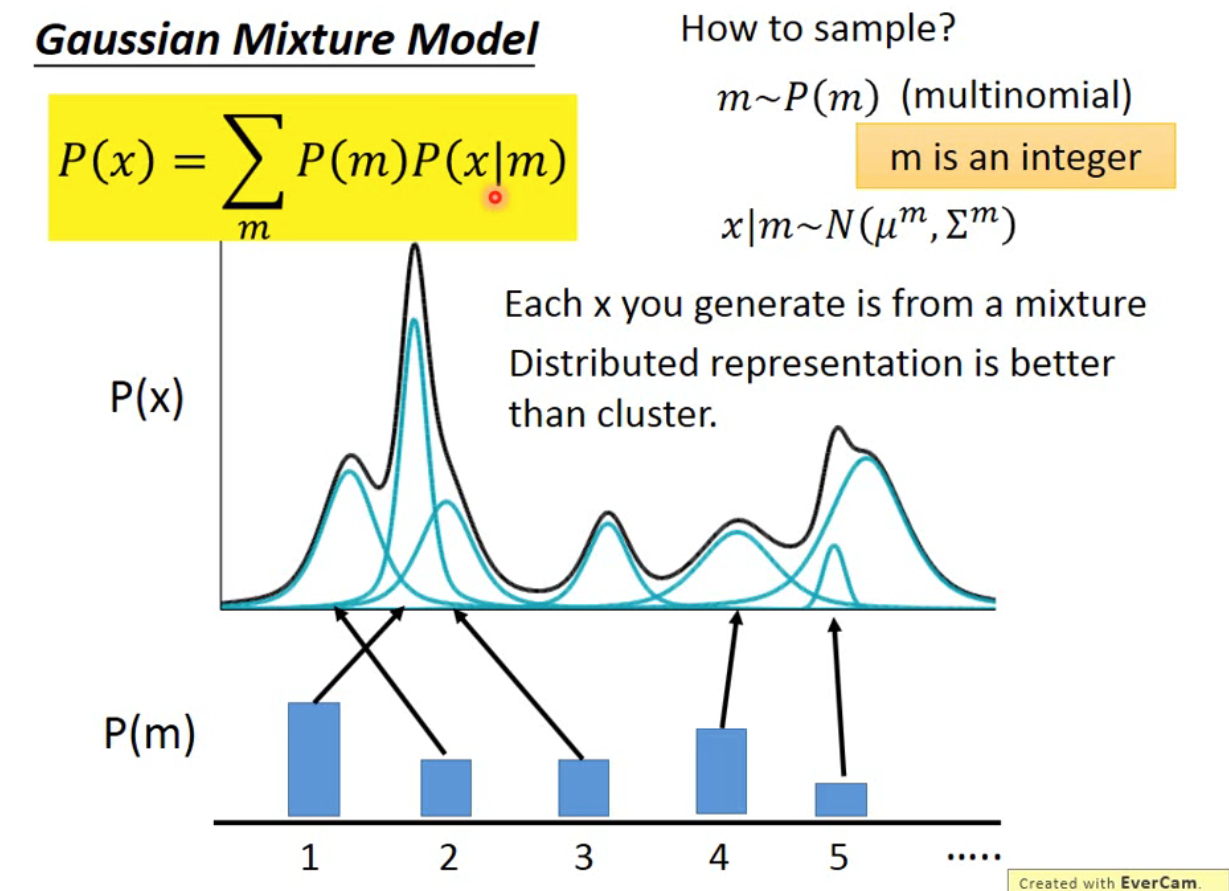
从几何分布的角度上讲，高斯混合模型假设分布$P(x)$由 K 个高斯分布叠加而成，每个高斯分布都有相应的权重

从概率学的角度分析，存在一个 latent variable（潜在变量）m，它是一个离散的随机变量，表示对应的样本$x$是由第 m 个高斯分布生成的概率。

举个例子，假设$m$满足如下分布：

$m$	1	2	…	K
$P(m)$	$P_1$	$P_2$	…	$P_k$

那么在进行采样时，先通过$m$采样出该使用哪一个高斯分布，然后再通过高斯分布采样出$x$

Distributive Representation

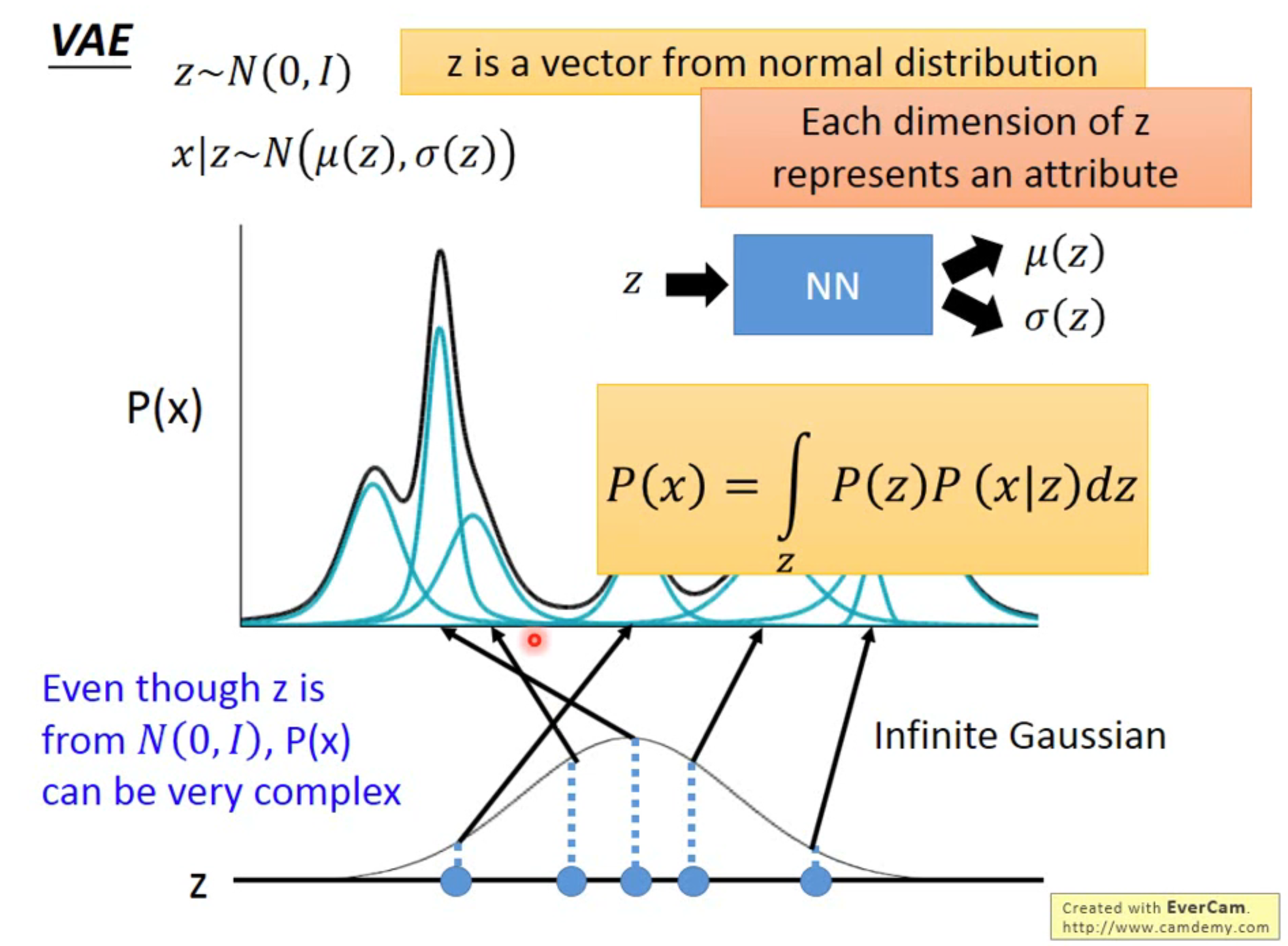
在 VAE 中，

1. sample 一个 $z$，$z$ 是来自 $(0，1)$ 高斯分布的一个向量，向量中的每个值代表一种特征
2. 通过 $z$，生成对应的 mean 和 variance，即找到对应的高斯分布

   \sigma \times z+\mu Q：为什么 z 是一个高斯分布？ A：分布可以是任意的，但是这里使用高斯分布比较符合直觉（大数定律与中心极限定理），同时神经网络的表达能力足够强，能够减少z的分布的 representation bias

   Q：如何找到 mean 和 variance？ A：通过一个神经网络结构，学习到对应的 mean 和 variance：

Note

对比 Gaussian mixture model，VAE 将离散分布的$m$变成了一个连续的正态分布$z$，并通过神经网络学习从 z 到高斯分布的映射，从而使 Gaussian mixture model 具有更好的拟合能力

Maximizing Likelihood

用概率模型来解释神经网络的过程，就是根据已知数据 $x$，最大化函数${\int }_{z}p(z)P(x|z)dz$，其中$\mu (z)，\sigma (z)$都是未知的，都是我们需要通过机器学习学习到的

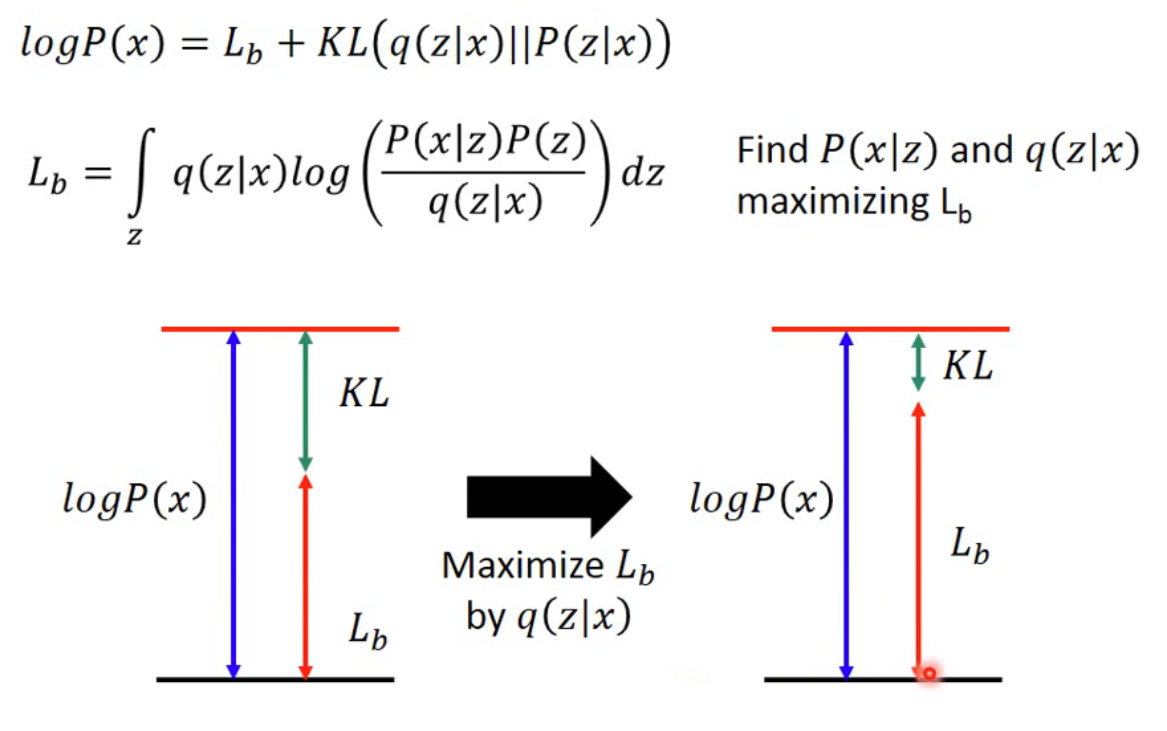
这部分是公式的推导过程，在这个过程中 $D_{KL}=(q(z|x)||P(z|x))\ge 0$，要保证 $\log P(x)$ 最大，因此剩余部分 ${\int }_{z}q(z|x)\log \left(\frac{P(x|z)P(z)}{q(z|x)}\right)dz$ 就称为 $L$ 的下边界（lower bound $L_b$），问题就转化为求 $max(L_b)$

除此之外，公式中还多出了变量$q(z|x)$，它表示的是 Auto Encoder 中的 encoder；同理，$P(x|z)$表示的是decoder

Warning

$L_b$ 表示其 $\log$ 似然的下边界，如果仅优化参数 $P(x|z)$ 对下边界求极大值，可能会导致边界变大，但实际似然估计值变小的情况

Note

• 使用 $q(z|x)$ 后，很好的解决了上述的问题
• $\log p(x)=\log {\int }_{z}P(z)P(x|z)dz$ 仅和 $P(x|z)$ 有关，因此若仅优化参数 $q(z|x)$ 会使 $\log P(x)$ 不变，$L_b$ 变大，$KL$ 变小，从而使 $L_b$ 更接近 $\log P(x)$
• 对应到网络中就是同时梯度下降 encoder 和 decoder 中的参数

Connection with Network

Note

使 KL 散度最小就相当于让 $P(z)$ 和 $q(z|x)$ 的分布越相似

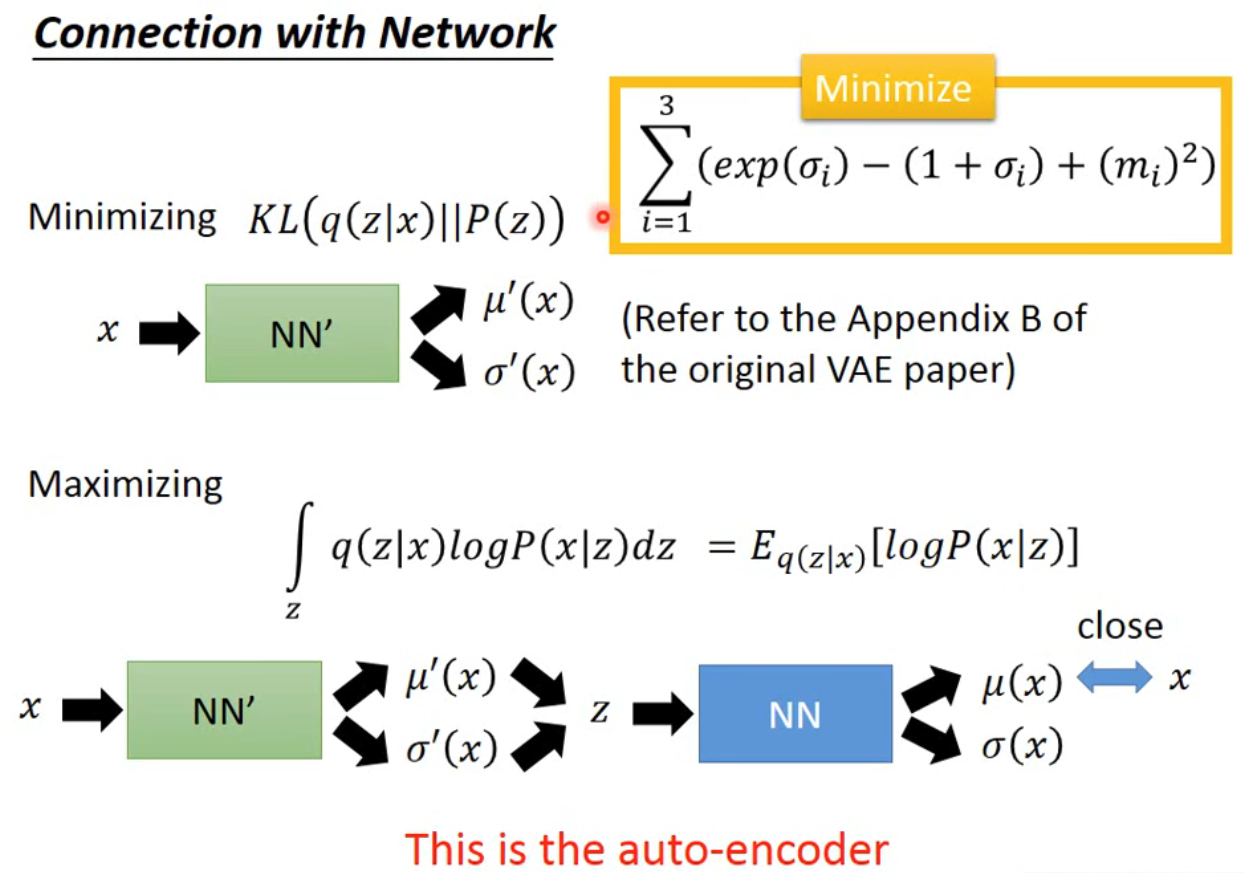
最后结合神经网络的实现，就可以得到相关损失函数的结论了

Conditional VAE

输入数字图片和其标签（Condition），生成带有同风格的其它数字

VAE的问题

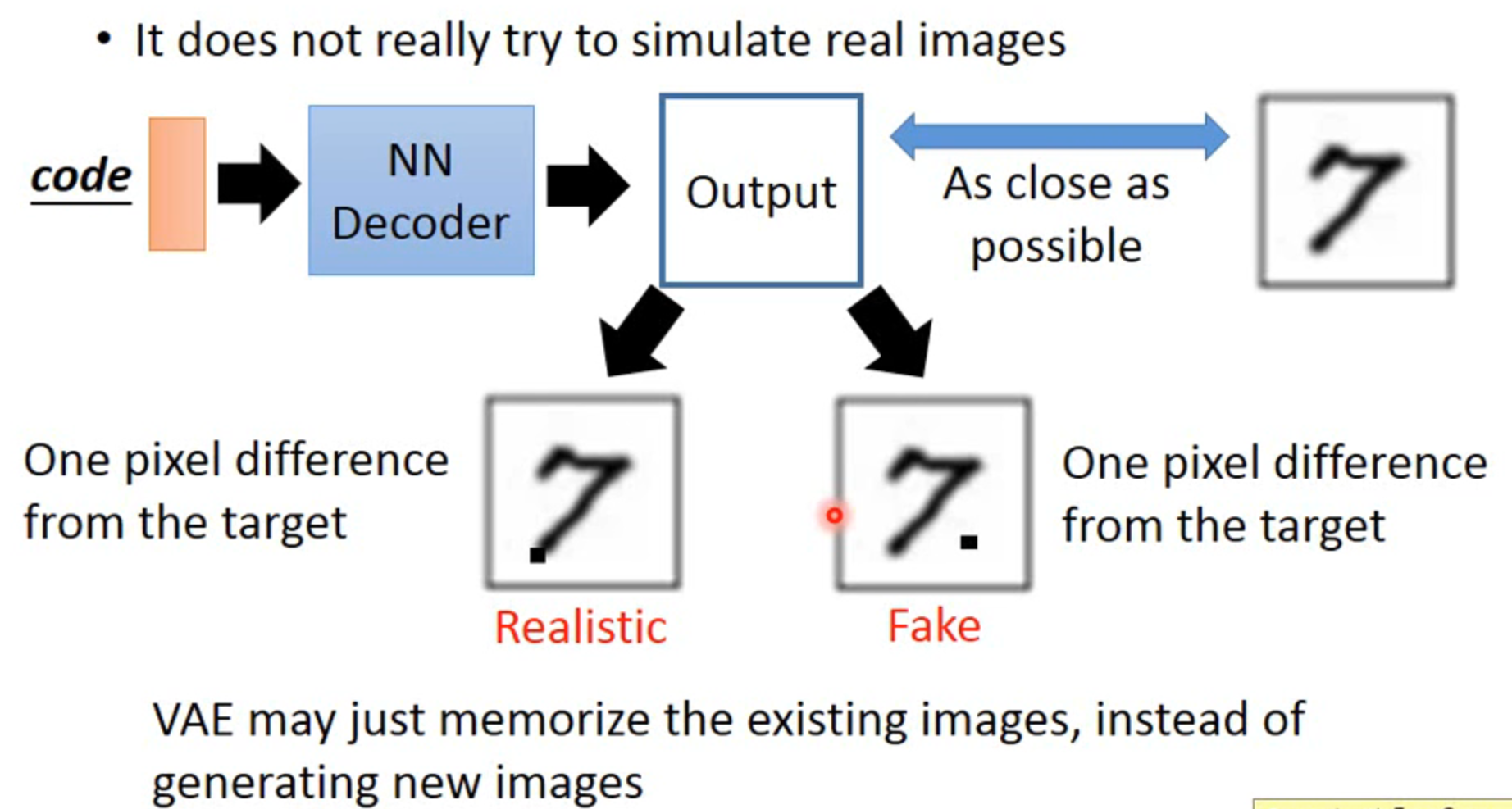
VAE 更适用于风格的模仿，并没有学习到生成的规则

库克距离*

在异常点检测中，库克距离是一个传统算法中的BaseLine

在线性回归中，我们通常使用最小二乘法来拟合数据，即找到一条直线（或者超平面）使得所有数据点到该直线的距离平方和最小。假设我们得到了一条线性回归模型，并用该模型对数据进行拟合，得到了一些残差。对于每一个数据点，我们可以计算出其残差（即该数据点的实际观测值与模型预测值之间的差），然后将这些残差平方和作为度量模型拟合好坏的指标。

然而，在实际数据中，可能存在一些异常值或者离群点，这些数据点的存在可能会对模型拟合结果产生较大的影响。例如，一个极端值可能会导致模型的斜率或截距发生较大的变化，因此我们需要一种方法来识别这些对模型产生较大影响的数据点。这时候，库克距离就可以发挥作用了。

库克距离的计算过程可以分为以下几步：

1. 对于每一个数据点，分别计算其残差。
2. 对于每一个数据点，假设我们将其排除后重新拟合模型，得到新的模型参数和残差。
3. 计算在该数据点被排除后，模型参数对应的标准化残差平方和（即残差平方和除以方差）的变化量。
4. 对于每一个数据点，计算其对应的库克距离。

具体而言，库克距离可以表示为：

$D_i=\frac{{\sum }_{j=1}^n({\hat{y}}_j-{\hat{y}}_{j(i)}{)}^2}{p\times MSE}\times \frac{h_{ii}}{(1-h_{ii}{)}^2}$

其中，$n$表示数据点的数量，${\hat{y}}_j$表示模型对第$j$个数据点的预测值，${\hat{y}}_{j(i)}$表示排除第$i$个数据点后模型对第$j$个数据点的预测值，$p$表示模型中参数的数量，$MSE$表示模型的均方误差，$h_{ii}$表示第$i$个数据点对于模型预测值的杠杆作用，即$h_{ii}$越大表示该数据点对模型参数的影响越大。

通过计算每个数据点的库克距离，我们可以找出那些对模型拟合影响较大的数据点，进一步分析这些数据点是否为异常值或者离群点。

GAN

视频空降

演化过程

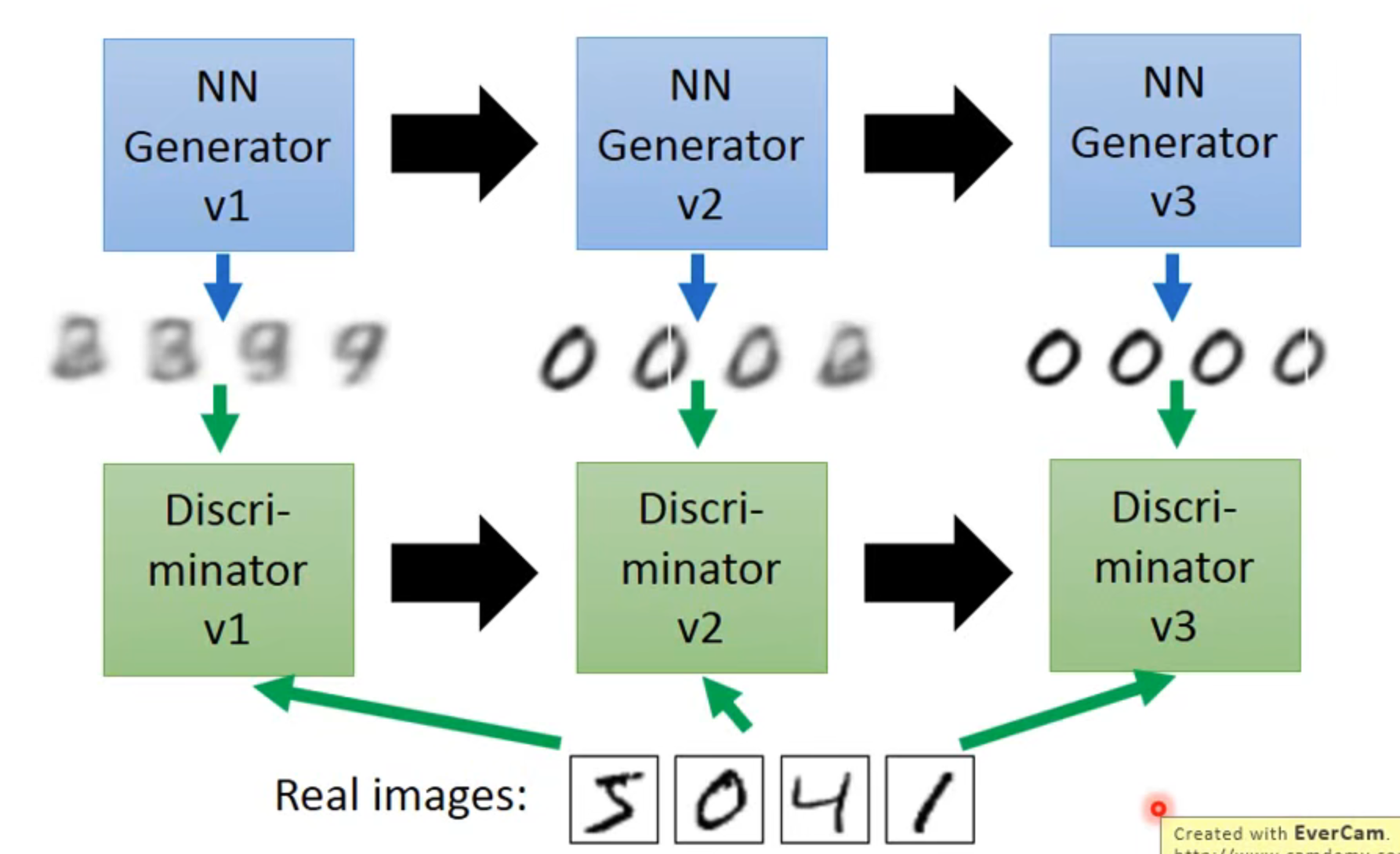
一个 GAN 由两个部分组成：Generator 和 Discriminator，以图片生成任务为例，Generator 可以生成一个图片，Discriminator 可以判别图片，具体步骤如下：

1. 由 Generator v1 生成图片
2. 交由 Discriminator v1 判断与真实图片（真实图片已给出）的距离（error）
3. 更新 Discriminator v1 参数，目的是让 Discriminator 能够判断出哪个是 Generator v1 生成的，哪个是真实图片
4. 再更新 Generator v1 的参数，目的是骗过 Discriminator ，让它判断不出来哪个是生成的，哪个是真实的
5. 如此往复…

• 特点：Generator 没有看过真实图片（但是通过反向传播建立从判别器到生成器的联系），它唯一做的事情是骗过 Discriminator

Discriminator

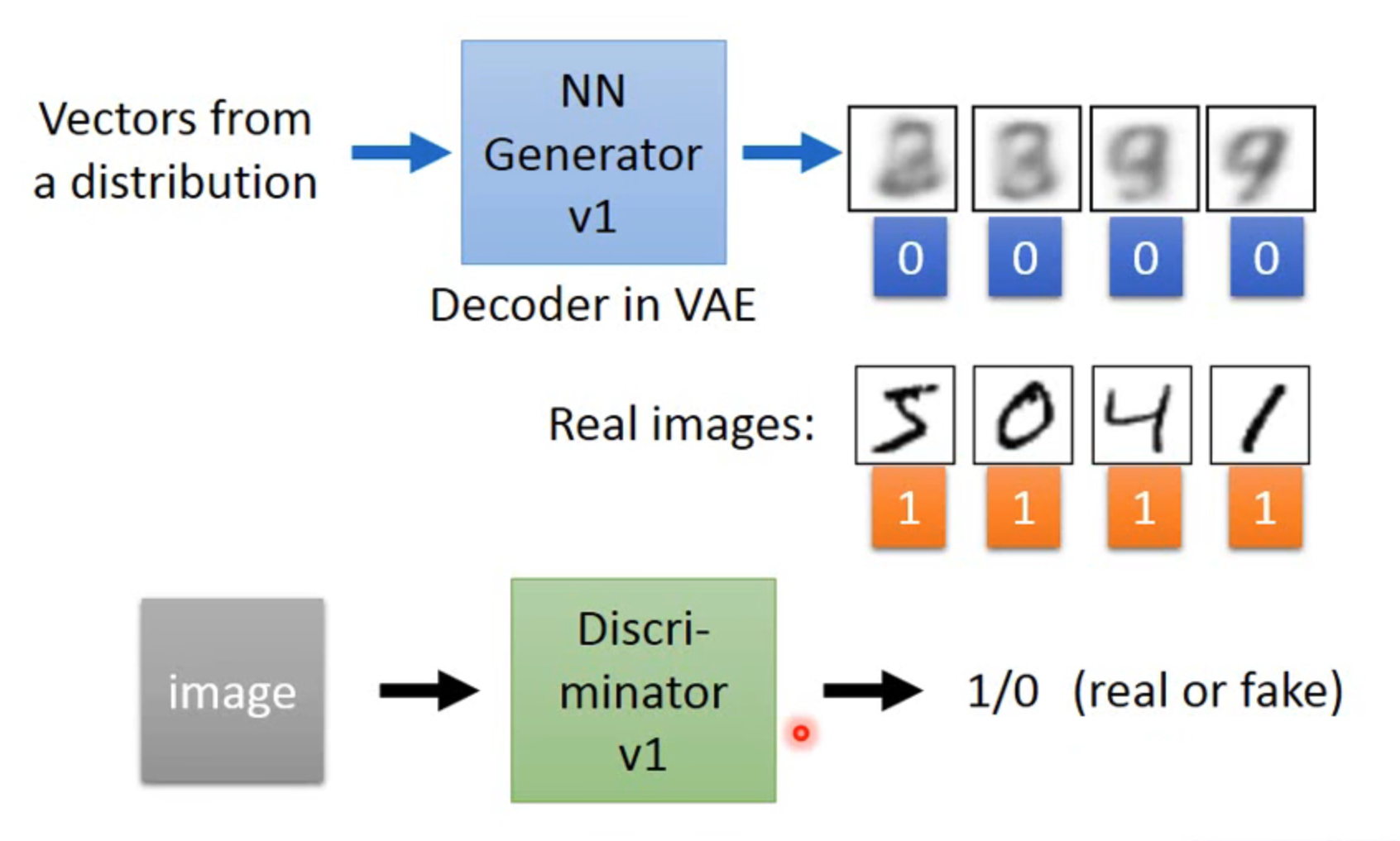
判别器的定义和传统的神经网络二分类类似，生成图片标注 0，真实图片标注为 1，输入一张图片，需要输出 0/1 来判断这张图片是生成图片还是真实图片

Generator

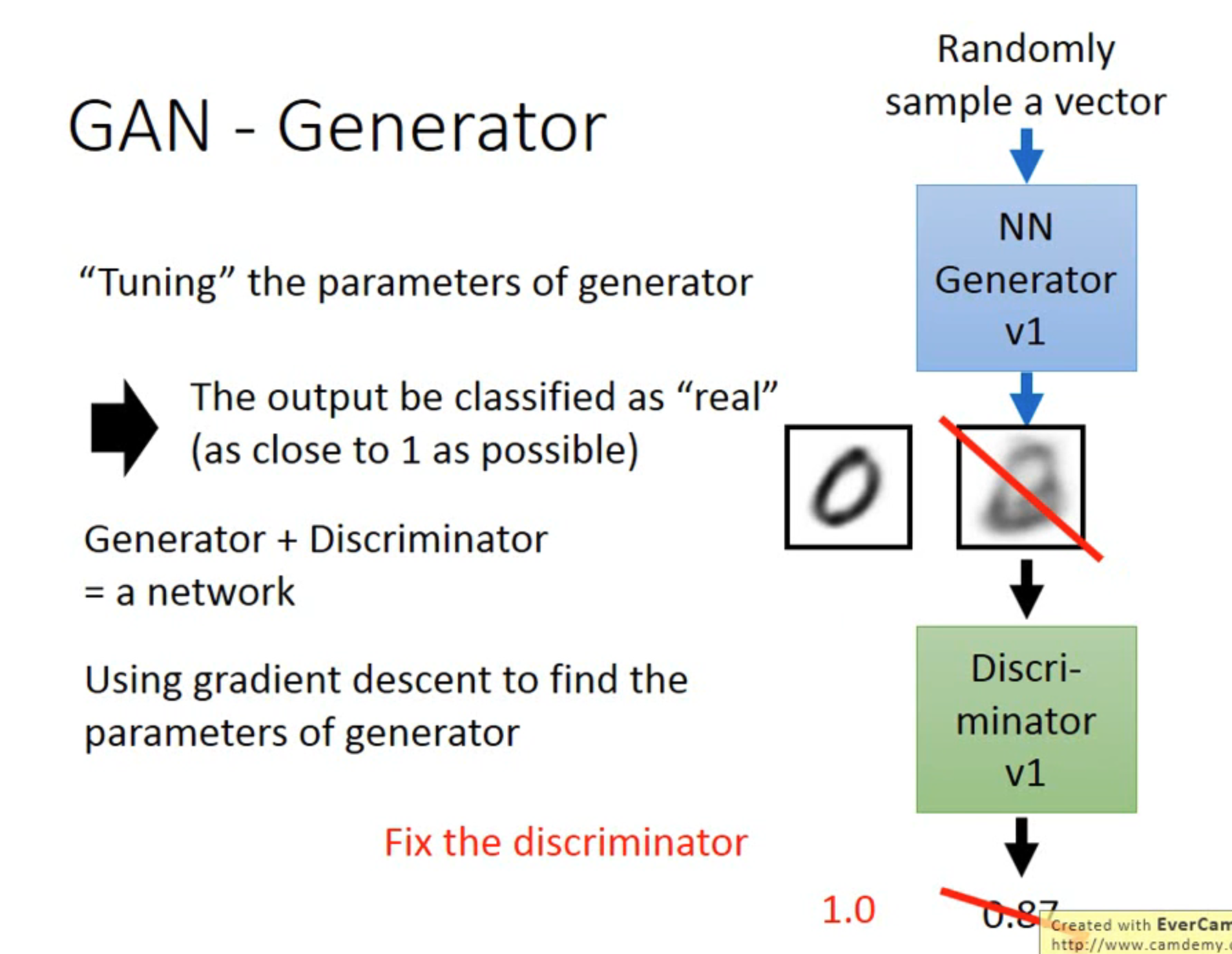
生成器部分最不同的就是参数的更新，我们把 Generator 和 Discriminator 看作一个整体，是一个更大的神经网络，然后进行反向传播，不同的是我们在反向传播时要 freeze 判别器的权重，只更新生成器的

举个🌰

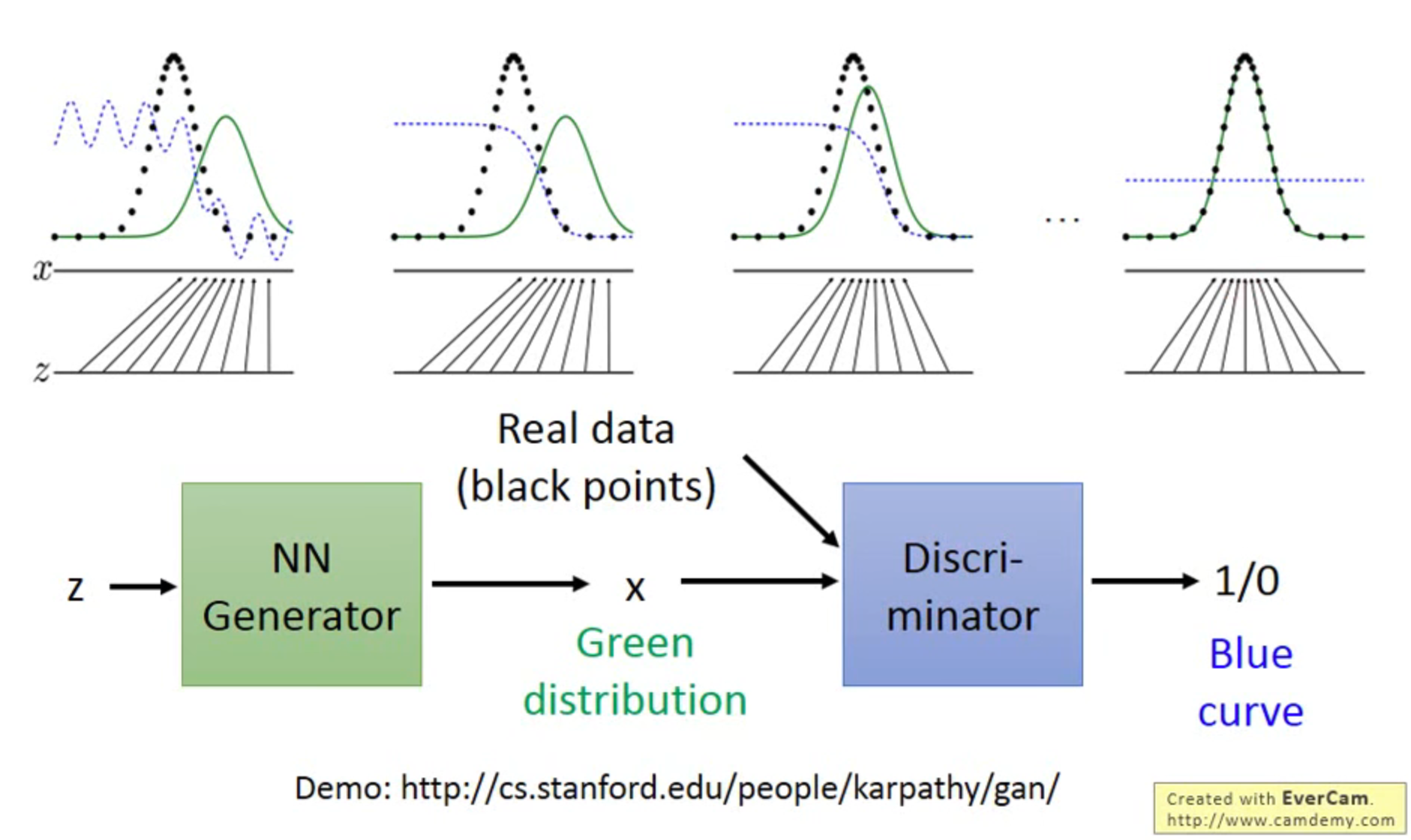
z 是一个一维的均匀分布的随机采样，经过生成器得到 x ，x 的概率分布如图中绿色曲线所示，黑色离散点分布是真实数据的抽样情况，根据 GAN 的定义，需要将 x 与真实数据进行对比，计算距离损失，并更新判别器的参数，从第二个图表中可以看出判别器认为靠右的数据可能是假的；之后固定判别器参数，更新生成器参数… 一直进行下去直到两个分布趋于一致

GAN 的缺点：

1. 生成器和判别器的对抗程度无法确定（有可能判别器很强，生成器一直没办法骗过判别器）
2. 虽然在这个例子中最后重合了，但也可能会出现一开始绿色曲线左移，逐渐贴合真实数据，然后一次大右移又远离真实数据

GAN 的缺陷

• GAN 非常难优化，因为生成的内容比较随机，且这种对抗训练的效果不见得好
• 没有指标衡量生成内容的好坏，因此很难做评估
• 如果判别器质量很差，可能无法训练出来比较好的生成器，因此要尽可能让判别器的鲁棒性提高