Chapter 1 线性空间与内积空间
线性空间
数域的定义
简单来说就是对四则运算封闭,则称为一个数域

线性空间的概念
- 给定非空集合,数域
- 在中定义了一种运算,称为加法,记为
- 在与之间定义了另一种运算,称为数乘,记为
- 如果这两种运算关于封闭,并且满足以下 8 条运算规律,则称是上的一个线性空间

Attention
注:非空集合内元素的分量是
- 线性空间的三个重要例子:
- 分量属于数域的全体 n 元数组

- 在实数域上,次数等于 n 的全体多项式

- 在实数域上,矩阵全体
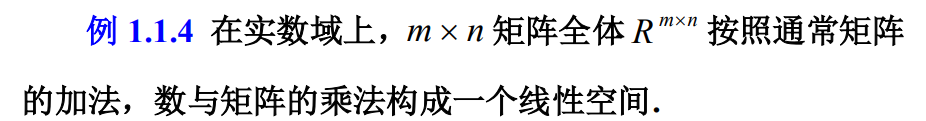
线性空间的性质
- 线性空间的零元素是唯一的
- 线性空间中的任一元素的负元素是唯一的
- 如果,则或
线性空间中向量的线性相关性
-
线性组合与线性表示:

-
向量组之间的等价关系:

-
线性相关和线性无关:

线性空间的基与维数
基、维数及坐标的定义

向量线性运算的坐标表示


- 两向量相加就是对应坐标向量分量相加
- 向量数乘就是每个分量乘以数
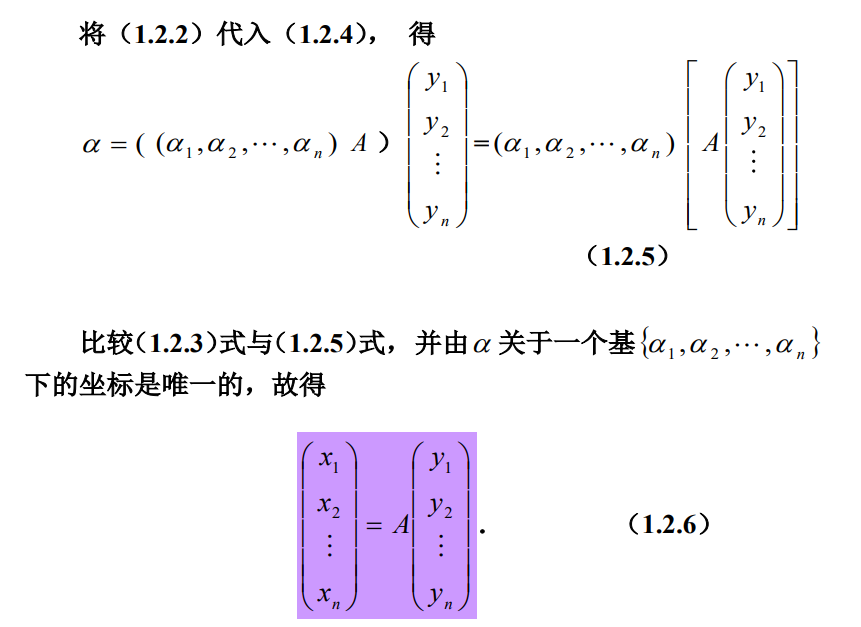
基变换与坐标变换
- 基变换、过渡矩阵概念


Attention
过渡矩阵放在基向量后面
- 坐标变换公式


Summary
- 基向量,A 为从向量 → 的过渡矩阵
- 对于该线性空间上一向量,其坐标变换为
过渡矩阵的性质
-
过渡矩阵的传递

-
过渡矩阵是可逆矩阵

-
若从到的过渡矩阵为,则从到的过渡矩阵为
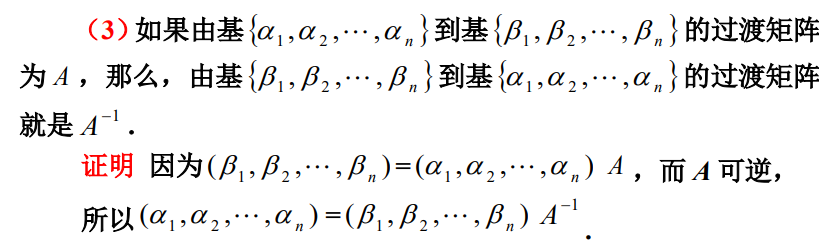
-
其它一些性质

线性子空间
线性子空间的概念

Summary
- 是线性空间的一个非空子集合
- 对于中的线性运算封闭
一些特殊的子空间
- 平凡子空间

- 生成子空间

子空间的交与和
-
交的概念

-
和的概念

>
>
这道例题结合了之前的生成子空间和子空间的交与和的概念
子空间的基和维数


>
dim (V_1+V_2) = dim V_1 + dim V_2 - dim(V_1 \cap V_2)



Summary
- 直和指的是空间中
- 直和的两个向量相互称为补空间
- 可以进行直和的空间叫做直和分解
内积空间
内积的定义与性质

Example
在欧氏空间中,内积为 但是在内积空间中,扩展了内积这一概念,内积变成了一种满足条件的任一方式
内积的性质

度量矩阵


Notice
正定:
广义定义:设 M 是 n 阶方阵,如果对任何非零向量 ,都有 ,其中 表示 的转置,就称 为正定矩阵。 正定的等价命题:
- 正定矩阵的行列式恒为正;
- 实对称矩阵 正定当且仅当 与单位矩阵合同;
- 若 是正定矩阵,则 的逆矩阵也是正定矩阵;
- 两个正定矩阵的和是正定矩阵;
- 正实数与正定矩阵的乘积是正定矩阵;
-
模的定义
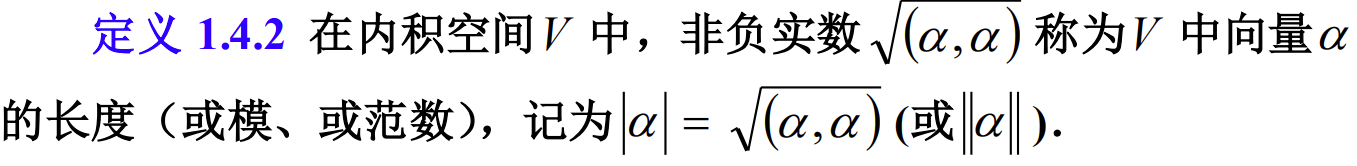
-
向量的单位化

-
模的一些性质



向量的正交性与 Schmidt 正交化方法
正交性
-
正交的定义

-
正交系的定义

-
正交系的一些性质


Schmit 正交化方法

Attention
标准正交基不唯一! 例如在中,也是一组正交基
正交基在坐标的应用


Notice
正交矩阵:如果(为单位矩阵,表示“矩阵的转置矩阵”)或,则阶实矩阵称为正交矩阵
空间的正交分解

>
这道题有几个难点:
- 按照题目所示,, 是线性无关的,因此可以把和当作一组基;
- 然后需要通过的标准正交基和正交补空间的性质来构造条件
- 最后得到正交补空间的基,从而求得正交补空间
线性空间的同构



- 同构映射的性质





Note
一个好记的“说法”: 对于任意两个维数相同的空间,都可以通过数域上的一组坐标做 1-1 的映射,那么根据映射的**”传递性“**,这两个空间一定可以建立一个 1-1 映射
Chapter 2 线性变换
我们把包含加法和数乘操作的线性空间到线性空间的映射叫做线性映射,而线性变换就是线性空间到自身的线性映射
线性变换的概念
线性变换的定义

Summary
根据上一章节的内容,到的映射满足维数相同的条件,所以是一个同构映射,且满足线性运算加法和数乘,因此变换被称为线性变换
- 一些特殊的线性变换

线性变换的性质

-
值域和核

A到B的映射,A中的元素a与B中的元素b对应,a叫原像,b叫像集合
-
值域和核的一些性质



Note
直观来理解,一个线性映射有可能把一个维度的原像映射成零向量,从而达到降维的效果
线性变换的运算


Attention
勘误:关于第(4)个运算规律里有一行是错的:


线性变换的矩阵
线性变换的矩阵表示



Attention
这里需要注意,不要和矩阵的基变换、坐标变换搞混;
- 基变换是从到,向量在基的坐标是,在基的坐标是,最后得到的坐标变换是
- 线性变换是从像向量到原像向量,在的坐标是,在的坐标是,最后得到的坐标变换是

Attention
这里注意不要和前者搞混 该定理说明,线性空间 中的线性变换 在两个不同基下的矩阵是相似的.反过来也可以证明,两个相似矩阵总可以看成某一线性变换在两个不同基下的矩阵.
Note
- 什么是相似? 则称相似
- 矩阵相似:判断特征值是否相等;判断行列式是否相等;判断迹是否相等;判断秩是否相等。
- 什么是合同? ,则称,合同
- 矩阵合同:设均为复数域上的 n 阶对称矩阵,则与在复数域上合同等价于与的秩相同;设均为实数域上的阶对称矩阵,则与在实数域上合同等价于与有相同的正、负惯性指数(即正、负特征值的个数相等)
>
- 第一问已知坐标变换,求线性变换在基下的矩阵
- 首先要求得坐标的变换公式
- 然后要求得线性变换下的矩阵
- 最后根据坐标和线性变换的关系求得矩阵
- 第二问已知变换矩阵,要求得变换矩阵
- 首先需要找到两个基的过渡矩阵
- 然后根据过渡矩阵和线性变换的关系求得
正交变换与酉变换
在内积空间中有一种特殊的线性变换,它保持向量的内 积不变,这种变换称为酉(正交)变换
正交矩阵与正交变换

-
正交矩阵的充要条件

-
一些线性变换的性质



酉矩阵与酉变换

Note
设 ,用表示以 A 的元素的共轭复数为元素组成的矩阵,其中表示元素属于复数域的全体矩阵组成的集合,按矩阵的加法和数与矩阵的数量乘法构成复数域上的线性空间; 则有:,其中表示对取转置称为的共轭转置矩阵
Note
和实数上的正交矩阵基本相同
正规矩阵





Chapter 3 矩阵的 Jordan 标准形
本章主要讨论-矩阵的概念与基本性质,及其 Smith 标准形,然后利用-矩阵的理论导出矩阵的 Jordan 标准形,最后给出矩阵的 Cayley-Hamiltom 定理
-矩阵及其 Smith 标准形

- 多项式表示法

-矩阵和普通矩阵有很多概念是一样的:
-
秩的概念


-
逆矩阵的概念


Attention
注意,在阶-矩阵中,可逆必满秩,反之则不然(因为可逆条件比较苛刻,需要保证行列式为非零常数,而满秩只要非零即可)
-矩阵的初等变换与等价
-
初等变换

-
初等矩阵

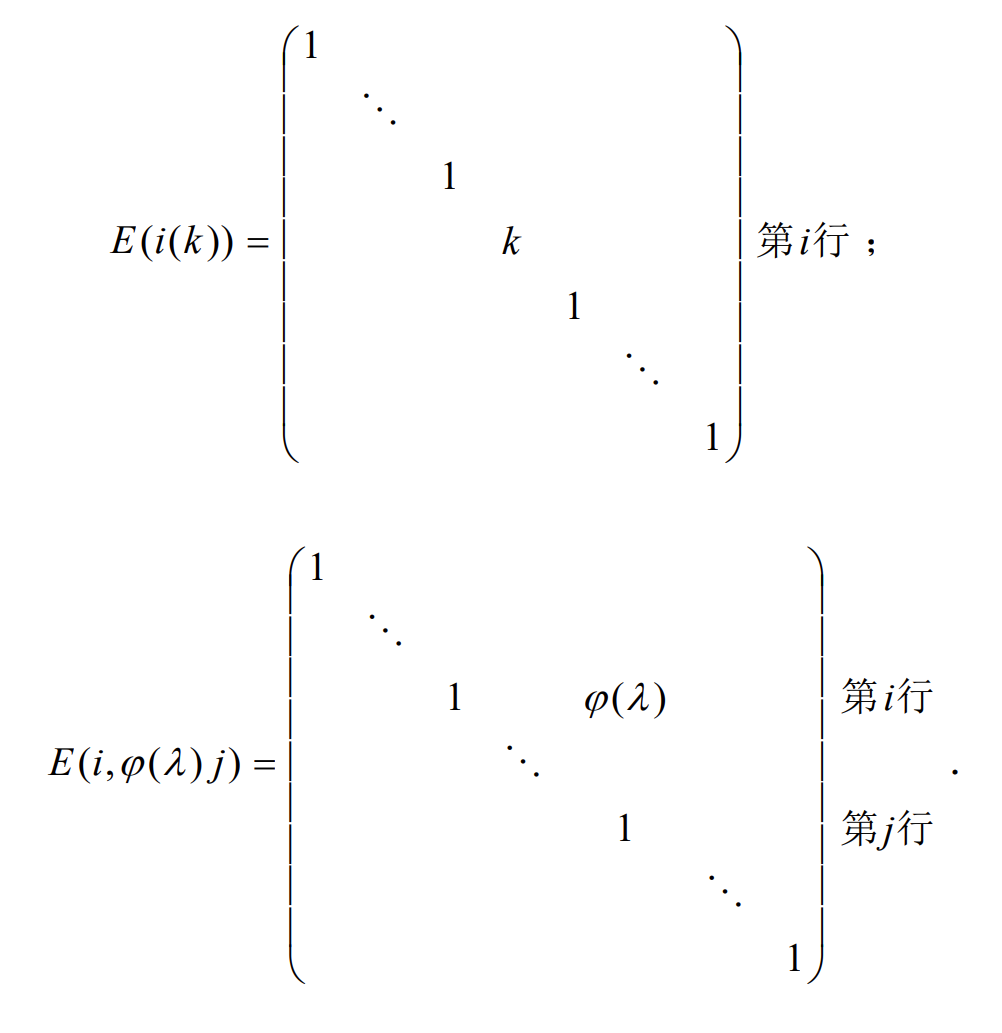
-
初等矩阵的性质


-
-矩阵等价


Attention
- -矩阵的等价关系与一般等价关系一样,满足自反性,对称性和传递性
- 注意,若,则有

Attention
3.1.4 的逆命题不成立,即秩相等,但不一定等价
-矩阵的 Smith 标准形

表示整除的意思,表示可以整除
Note
如何化矩阵为标准形?
- case 1: 能整除一切 在这种情况下用第一行及第一列消去其他元素
- case 2: 不能整除一切,可以利用初等变换降低次数,具体分为三种情况:
- 第一行存在元素不能被整除: 互换列
- 第一列存在元素不能被整除: 互换行
- 不能被整除: 通过消除元素,变成上面两种情况
-
不变因子

-
初等因子

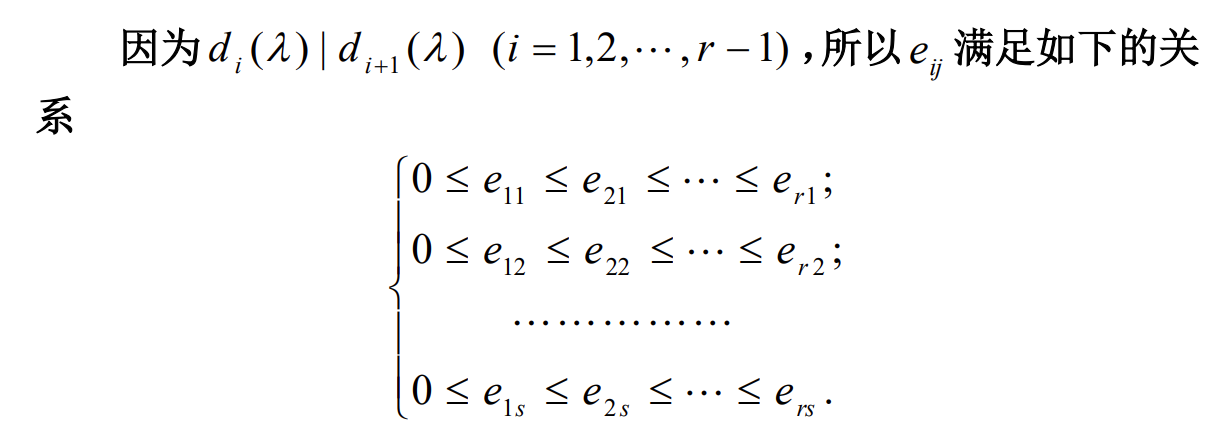
Note
一共有,因此每一列有个
- 一些关于不变因子和初等因子的性质

Example
关于如何找到不变因子的例题:
>
-矩阵的行列式因子


Example
利用行列式因子求解不变因子的方法
这题利用了阶行列式因子的性质,先求出了该-矩阵的阶行列式因子,然后根据定理 3.2.1 的性质,得到不变因子为以此类推
相伴矩阵的计算
>
>
>
这道题的难点在于矩阵本身是无限的,因此对矩阵本身很难看出来其结构;其次,需要对矩阵进行一次变换,将矩阵简化才能计算;最后需要对不变因子、初等因子的概念有很深刻的认识,才能知道前个不变因子都为
矩阵的 Jordan 标准形

矩阵的相似条件


-
前面学习的行列式因子,不变因子和初等因子终于排上用上了 😭

-
、 矩阵相似的充分必要条件

矩阵的 Jordan 标准形

>

>
-
Jordan 型矩阵的初等因子
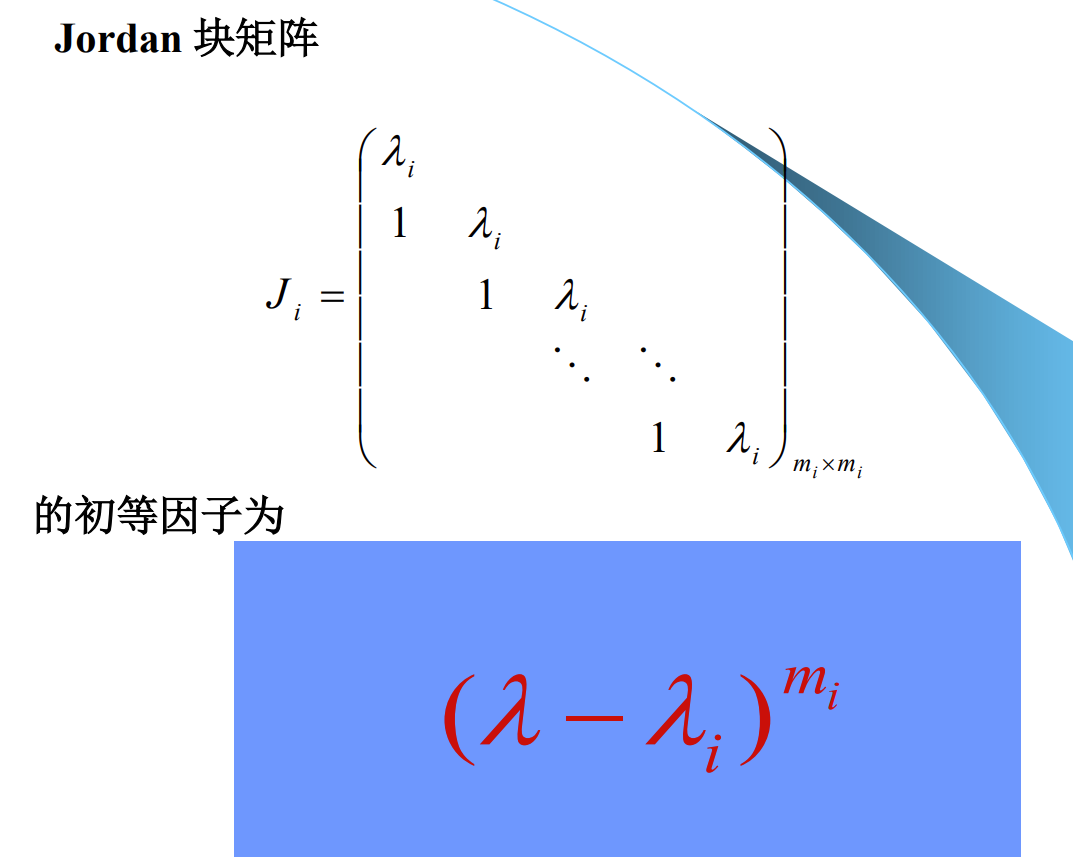 相关证明过程:
相关证明过程:


-
矩阵的 Jordan 标准形 每一个方阵都与一个 Jordan 型矩阵相似
 证明:
证明:

由定理3.3.3可得J与A相似引用错误,应该是定理 3.3.1需要注意,这里
初等因子可以得到对应的Jordan 标准形
由
-
重要推论

>
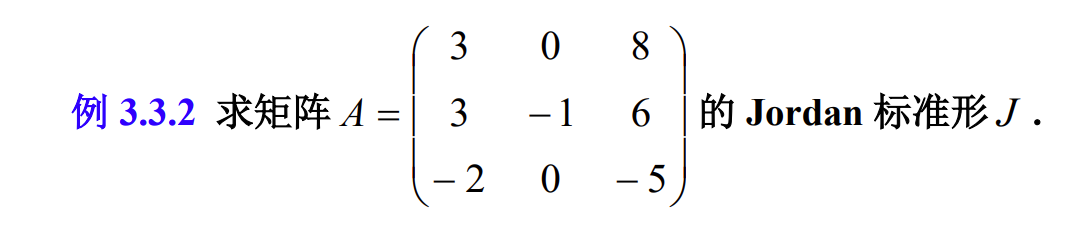 >
> 
- 总结求 Jordan 标准形的步骤:
- 求得初等因子形式为 ,其中 就是 Jordan 标准形的 表示其重复次数,
- 按照初等因子中的 写出 Jordan 标准形的大致结构
- 并按照 Jordan 标准形补
- 总结求 Jordan 标准形的步骤:
求得 Jordan 标准形后,需要求得相似变换的变换矩阵,在分块 Jordan 标准形中,有如下分块求法:

>
>
>
相似矩阵计算总结:
- 计算 Jordan 标准形
- 根据 列出方程组
- 解方程组
- 先解齐次线性方程组,再解非齐次线性方程组
- 非齐次线性方程组中,先解向量已知的,再解向量未知的
Cayley-Hamiltom 定理与最小多项式
Cayley-Hamiltom 定理

>
>
矩阵的最小多项式
- 零化多项式


>

- 最小多项式
 定理 3.4.3 相似矩阵有相同的最小多项式
定理 3.4.4 阶矩阵 的最小多项式是唯一的
定理 3.4.5
(1) 阶矩阵 的最小多项式的根必定是 的特征根
(2) 的特征根必定是 的最小多项式的根
定理 3.4.3 相似矩阵有相同的最小多项式
定理 3.4.4 阶矩阵 的最小多项式是唯一的
定理 3.4.5
(1) 阶矩阵 的最小多项式的根必定是 的特征根
(2) 的特征根必定是 的最小多项式的根 - 重要推论


Chapter 4 矩阵分解
把矩阵分解为形式比较简单或具有某种特性的一些矩阵的乘积,一方面能明显地反映出原矩阵的某些数值特征,如矩阵的秩、行列式、特征值及奇异值等,另一方面分解的方法与过程往往提供了某些有效的数值计算方法和理论分析根据
矩阵的满秩分解
-
满秩分解

-
平凡分解

-
满秩矩阵存在的条件

A的满秩分解不是唯一的 定理 4.1.1 的证明过程表明,可以使用矩阵的初等行变换方法求矩阵的满秩分解矩阵
-
求满秩分解的方法

>
 总结一下求满秩矩阵的步骤:
目标:得到一个满秩分解,使得
总结一下求满秩矩阵的步骤:
目标:得到一个满秩分解,使得A=FG1. 矩阵A先经过初等变换矩阵P,得到一个阶梯矩阵B,并计算出rank(A)=r2. 取B中前r行做为矩阵G3. 再求得P^{-1},取P^{-1}的前r列作为矩阵F,即得满秩分解F和G,满足A=FG快速求得 F 的方法: >
> 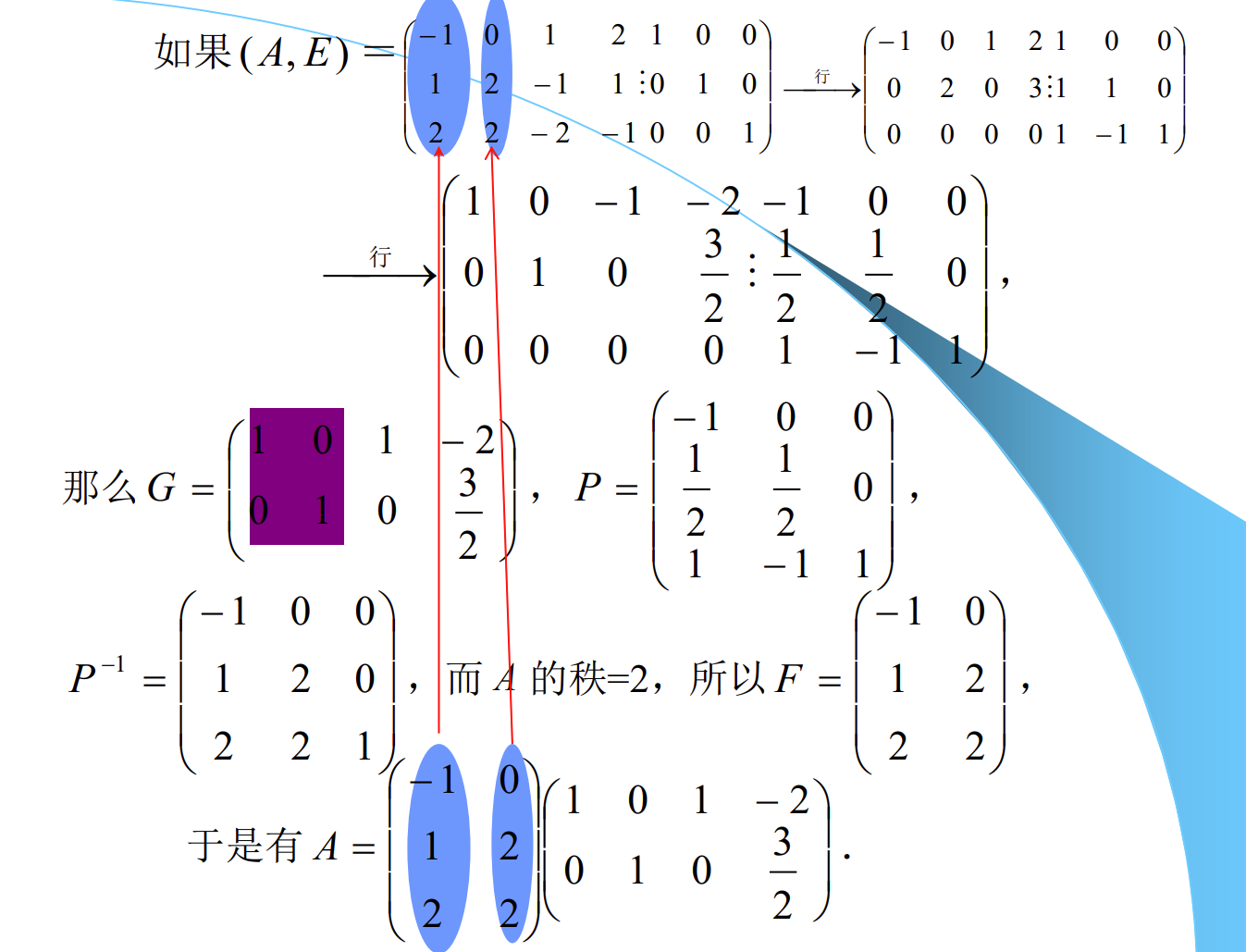 从图中可以看出
从图中可以看出 G的阶梯矩阵在第一列和第二列的第一个阶梯都不为0,因此可以把A中的第1列和第2列作为F
矩阵的奇异值分解
-
一些引理

取共轭(实部不变,虚部取负) 2. 进行一次普通转置
H 表示共轭转置,共轭转置的步骤: 1. 对每个元素
-
奇异值

>
 由例子可以看出来,谱范数(二范数)
由例子可以看出来,谱范数(二范数)= max\{\sigma_i\}, (i=1,2,\dots,n) -
奇异值分解
 “简单”证明:
“简单”证明:

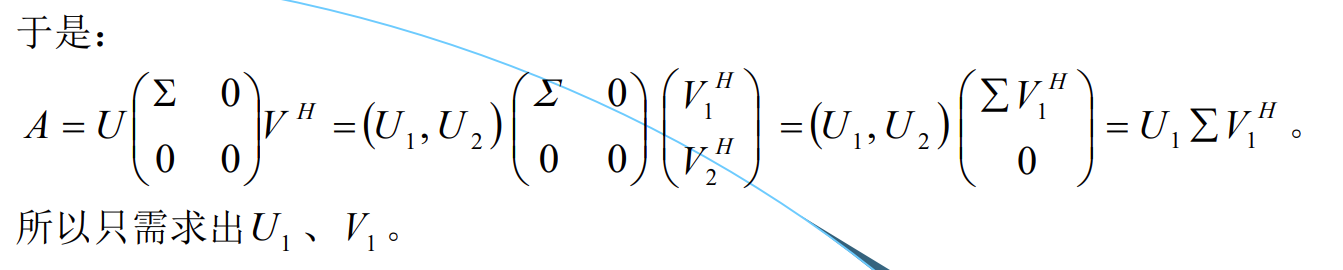 奇异值分解步骤:
奇异值分解步骤:

>
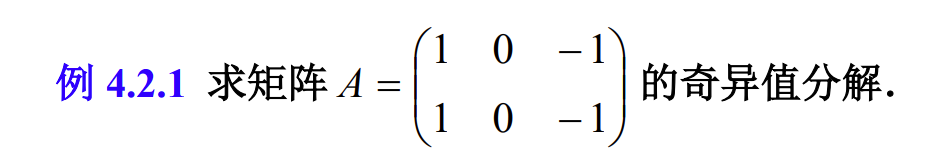 >
>  >
> 








