最优化理论

Notice

参考书籍：《最优化方法及其 Matlab 程序设计》——马昌凤

全篇符号定义

最优化理论基础

最优化问题的数学模型

最优化模型可以由目标函数和限制条件两部分组成

本书主要考虑非线性规划，非线性规划又分为：

1. 无约束优化问题
2. 等式约束优化问题
3. 非等式约束优化问题

还有一些特殊的情况：

1. 二次规划：目标函数为二次函数而约束函数都是线性函数
2. 线性规划：目标函数和约束函数都是线性函数

向量和矩阵范数

Note

详细内容可以参考数值分析的内容

范数的条件:

1. $\Vert x\Vert \ge 0,\Vert x\Vert =0\iff x=0$

2. $\Vert \lambda x\Vert =|\lambda |\Vert x\Vert ,\lambda \in \mathbb{R}$

3. $\Vert x+y\Vert \le \Vert x\Vert +\Vert y\Vert$

4. $\Vert AB\Vert \le \Vert A\Vert \Vert B\Vert ,A,B\in {\mathbb{R}}^{n\times n}$ 如果一矩阵范数 $\Vert \cdot {\Vert }_{\mu }$ 相对于某向量范数 $\Vert \cdot \Vert$ 满足下面的不等式

5. $\Vert Ax\Vert \le \Vert A{\Vert }_{\mu }\Vert x\Vert ,x\in {\mathbb{R}}^n$

   

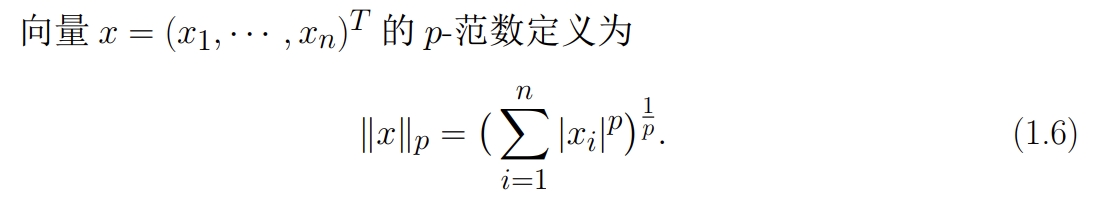
常用向量范数：

• 1-范数：$\Vert x{\Vert }_1={\sum }_{i=1}^n|x_i|$
• 2-范数：$\Vert x{\Vert }_2=({\sum }_{i=1}^n|x_i{|}^2{)}^{\frac{1}{2}}$
• $\infty$ 范数：$|x{|}_{\infty }=\underset{1\le i\le n}{\max }|x_i|$
• 说明

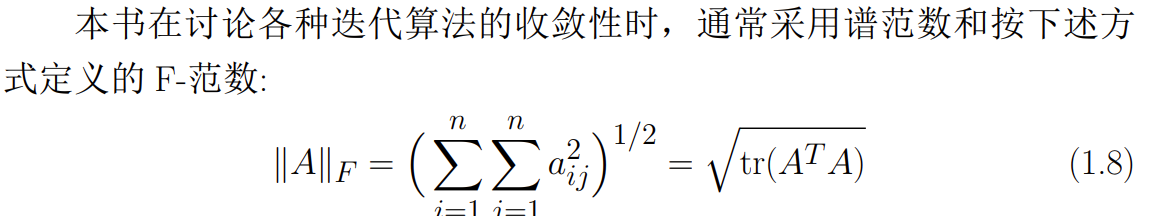
收敛性证明

• 向量范数的等价定理

• 矩阵范数的等价定理

• 收敛性描述

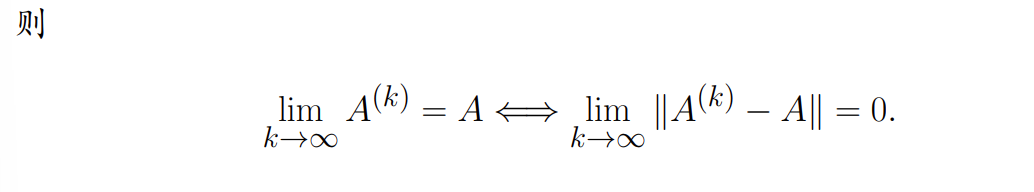
函数的可微性与展开

1. 一阶导数（梯度）
2. 二阶导数（Hesse 矩阵） 若梯度 $\nabla f(x)$的每个分量函数 在 $x$ 都连续, 则称 𝑓 在 𝑥 一阶连续可微；若 Hesse 阵 ${\nabla }^{2}f(x)$ 的各个分量 函数都连续，则称 $f$ 在 $x$ 二阶连续可微. 若 $f$ 在开集 $D$ 的每一点都连续可微，则称 $f$ 在 $D$ 上一阶连续可微；若 $f$ 在开集 $D$ 的每一点都都二阶连续可微，则称 $f$ 在 $D$ 上二阶连续可微.

Note

由上述定义不难发现，若$f$在$x$二阶连续可微，则 Hesse 矩阵是对称阵

向量值函数的可微性及中值定理

• Jacobi 矩阵的定义

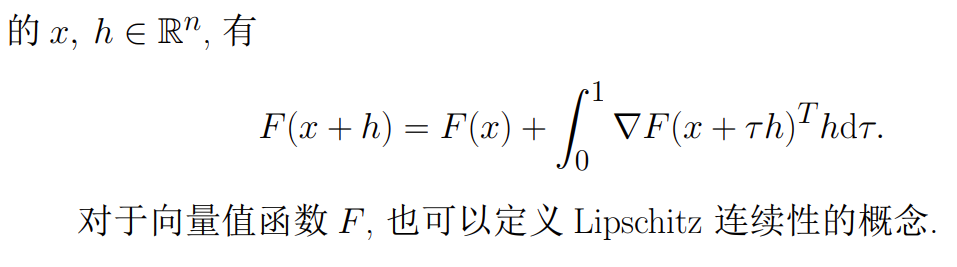
• Lipschitz 连续的定义

• 向量值函数的中值定理 由上面的结论可以得到下面的推论：

凸集与凸函数

Note

简单来说，凸集就是一个非空集合，任意连接其中两点的线段，仍属于该集合

• 凸集的基本性质

• 凸包的定义

• 锥和凸锥的定义

• 凸函数的定义

Note

凸函数的定义实际上和之前高数中凸函数的定义（$f(\frac{x+y}{2})\le \frac{f(x)+f(y)}{2}$）类似，这是$\lambda =2$的情况，这里使用$\lambda$更一般

• 凸函数的基本性质

• 判断凸性的几种方法

• 二阶导数判断凸性 推广到多元函数上：

无约束问题的最优性条件

• 极小点的定义

  Note

  一般来说，全局最优比较难求，因此通常只求局部极小点

• 一阶必要条件

• 二阶必要条件

• 二阶充分条件

  Note

  一般来说，目标函数的稳定点不一定是极小点。但对于目标函数是凸函数的无约束优化问题，其稳定点、局部极小点和全局极小点三者是等价的。

• 凸函数无约束优化问题——全局极小值点的充要条件

  Note

  需要注意和上面区分，凸函数已经表明有最小点，因此一阶必要条件直接变为充分必要条件

无约束优化问题的算法框架

• 一般算法框架：

  1. 给定初始化参数及初始迭代点 $x_0$ ，置 $k:=0$
  2. 若 $x_k$ 满足某种终止准则, 停止迭代, 以$x_k$作为近似极小点
  3. 通过求解 $x_k$ 处的某个子问题确定下降方向 $d_k$
  4. 通过某种搜索方式确定步长因子 ${\alpha }_k$ , 使得 $f(x_k+{\alpha }_k{d}_k)<f(x_k)$
  5. 令 $x_k+1:=x_k+{\alpha }_k{d}_k,k:=k+1$, 转步 2

• 下降方向 若目标函数 $f$ 是一阶连续可微的, 则判别 $d_k$ 是否为下降方向将有更为方便的判别条件：

• 收敛性

• 收敛速度

• 终止条件

线搜索技术

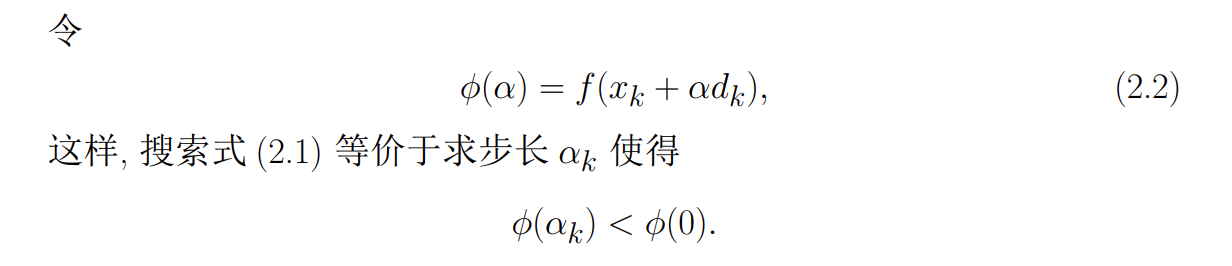
线搜索技术分为两种：

1. 精确线搜索

   基本思想：首先确定包含问题最优解的搜索区间，然后采用某种插值或分割技术缩小这个区间，进行搜索求解

   

   \alpha_k是极小值，因此关于其的导数为0

   因为这里的

2. 非精确线搜索

搜索区间

Note

这里强调了极小化问题，及单峰区间/单峰函数的概念，${\alpha }^{\ast }$是一个极小点

进退法确定搜索区间

其基本思想是从一点出发，按一定步长，试图确定函数值呈现 “高-低-高”的三点，从而得到一个近似的单峰区间

Attention

这个算法出现了笔误，step4 中，应为 $a=min\{\alpha ,{\alpha }_{k+1}\},b=max\{\alpha ,{\alpha }_{k+1}\}$

精确线搜索

精确线搜索分为两类：一类是使用导数的搜索，如插值法，牛顿法及抛物线法等；另一类是不用导数的搜索，如 0.618 法（黄金分割法），分数法及成功-失败法等，本书仅介绍 0.618 法和二次插值逼近法

黄金分割法

黄金分割法也称为 0.618 法，其基本思想是通过试探点函数值得比较，是包含极小点的搜索区间不断缩小。该方法仅需要计算函数值，适用范围广，使用方便

• 公式推导

• 算法步骤

  t = 0.618，故 0.618 法只是线性收敛的，即这一方法的计算效率并不高。但该方法每次迭代只需计算一次函数值的优点足以弥补这一缺憾

  值得说明的是，由于每次迭代搜索区间的收缩率是

二次插值法

• 算法步骤

非精确线搜索

线搜索技术是求解许多优化问题下降算法的基本组成部分，但精确线搜索往往需要计算很多的函数值和梯度值，从而耗费较多的计算资源。特别是当迭代点远离最优点时，精确线搜索通常不是十分有效和合理的。对于许多优化算法，其收敛速度并不依赖于精确搜索过程。因此，既能保证目标函数具有可接受的下降量又能使最终形成的迭代序列收敛的非精 确线搜索变得越来越流行。本书着重介绍非精确线搜索中的 Wolfe 准则和 Armijo 准则

Wolfe 准则

Note

强 Wolfe 准则表明, 由该准则得到的新的迭代点 $x_{k+1}=x_k+{\alpha }_k{d}_k$ 在 $x_k$ 的某一邻域内且使目标函数值有一定的下降量

Armijo 准则

• 算法步骤

线搜索法的收敛性

• 算法步骤

  >

• 非精确线搜索法的收敛性

• 精确线搜索的收敛性

最速下降法和牛顿法

最速下降法

> d_k是负梯度的方向，但d_k \ne -\nabla f(x_k)，需要把梯度改为单位向量，因此公式应该变为d_k=-\frac{\nabla f(x_k)}{\Vert \nabla f(x_k) \Vert}

• 算法步骤

• 最速下降法全局收敛定理

  > d_k 只是下降方向，但究竟需要多少步长是由 \alpha 确定的，因此需要结合线搜索方法找到合适的\alpha

• 收敛速度估计

  \kappa趋近于 1，则收敛速度会很快，但若 H 为病态时，算法收敛速度很缓慢

  结论：如果

牛顿法

跟最速下降法一样，牛顿法也是求解无约束优化问题最早使用的经典算法之一。其基本思想是用迭代点 $x_k$ 处的一阶导数（梯度）和二阶导数（Hesse 阵）对目标函数进行二次函数近似，然后把二次模型的极小点作为新的迭代点，并不断重复这一过程，直至求得满足精度的近似极小点

• 公式推导

  G^{-1}_kd=-g_k，在实际计算中可通过先解 G_kd = - g_k 得 d_k , 然后令 x_k+1 = x_k + d_k 来避免求逆（详细解法可以参考 Chapter 6. 线性方程组的直接解法）

  在迭代公式（3.4）中每步迭代需要求 Hesse 阵的逆

• 基本牛顿法的算法步骤 牛顿法最突出的优点是收敛速度快，具有局部二阶收敛性

• 阻尼牛顿法的算法步骤

• 全局收敛定理

修正牛顿法

从上一节的分析可知，牛顿法具有不低于二阶的收敛速度，这是它的优点。但该算法要求目标函数的 Hesse 阵 $G(x)={\nabla }^{2}f(x)$ 在每个迭代点 $x_k$ 处是正定的，否则难以保证牛顿方向 $d_k=-G_k^{-1}{g}_k$ 是 $f$ 在 $x_k$ 处的下降方向

修正的途径之一是将牛顿法和最速下降法结合起来，构造所谓的”牛顿-最速下降混合算法“

• 算法步骤

共轭梯度法

前面介绍的最速下降法和牛顿法都具有其自身的局限性，本章将要介绍的共轭梯度法是介于最速下降法与牛顿法之间的一种无约束优化算法，它具有超线性收敛速度, 而且算法结构简单, 容易编程实现。此外，跟最速下降法相类似，共轭梯度法只用到了目标函数及其梯度值，避免了二阶导数( Hesse 阵）的计算，从而降低了计算量和存储量，因此它是求解无约束优化问题的一种比较有效而实用的算法

共轭方向法

共轭方向法的基本思想是在求解 $n$ 维正定二次目标函数极小点时产生一组共轭方向作为搜索方向，在精确线搜索条件下算法至多迭代 $n$ 步 即能求得极小点，经过适当的修正后共轭方向法可以推广到求解一般非二次目标函数情形

• 共轭方向

  Note

  • 显然, 向量组的共轭是正交的推广, 即当 $G=I$(单位阵) 时, 上述定义 变成向量组正交的定义
  • 向量组的共轭是正交的推广，对称正定矩阵 $G$ 的共轭向量组必然是线性无关的

• 算法步骤

  n 步内即可求得其唯一的极小点。这种能在有限步内求得二次函数极小点的性质通常称为二次终止性

  从定理 4.1 可知，在精确线搜索下，用算法 4.1 求解正定二次目标函数极小化问题（4.1），至多在

共轭梯度法

共轭梯度法是在每一迭代步利用当前点处的最速下降方向来生成关于凸二次函数 $f$ 的 Hesee 阵 $G$ 的共轭方向，并建立求 $f$ 在 $R^n$ 上的极小点的方法。这一方法最早是由 Hesteness 和 Stiefel 于 1952 年为求解对称正定线性方程组而提出来的，后经 Fletcher 等人研究并应用于无约束优化问题取得了丰富的成果，共轭梯度法也因此成为当前求解无约束优化问题的重要算法类

公式推导：

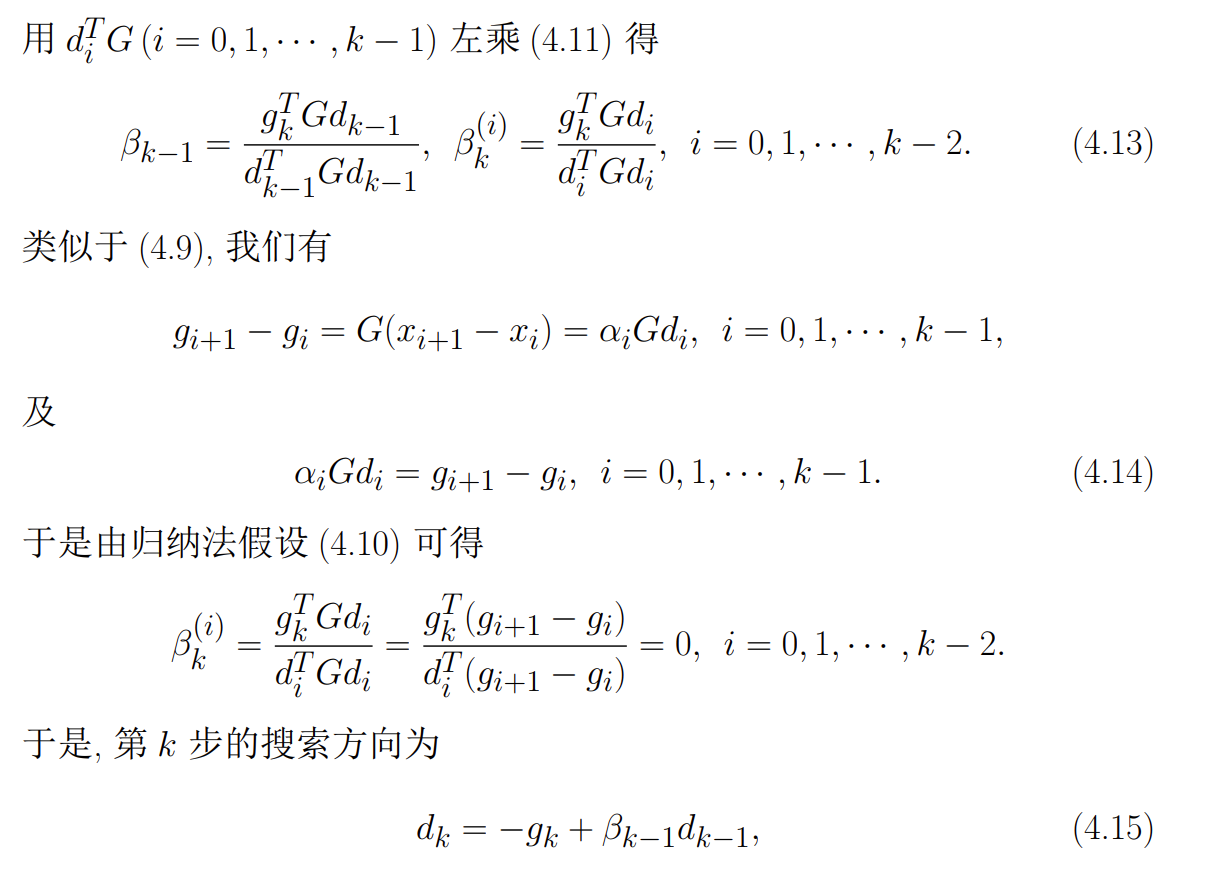
• 最终结论：

• 算法步骤

  

  共轭梯度法在精确线搜索和非精确线搜索下都是收敛的

拟牛顿法

第 3 章所介绍的牛顿法的优点是具有二阶收敛速度，但当 Hesse 阵 $G(x_k)={\nabla }^{2}f(x_k)$ 不正定时，不能保证所产生的方向是目标函数在 $x_k$ 处的下降方向。特别地，当 $G(x_k)$ 奇异时，算法就无法继续进行下去。尽管修正牛顿法可以克服这一缺陷，但其中的修正参数 ${\mu }_k$ 的选取很难把握，过大或过小都会影响到收敛速度。此外，牛顿法的每一迭代步都需要目标函数的二阶导数，即 Hesee 阵，对于大规模问题其计算量是惊人的

本章即将介绍的拟牛顿法克服了这些缺点，并且在一定条件下这类算法仍然具有较快的收敛速度—超线性收敛速度

拟牛顿法及其性质

• 基本思想

• 对称秩 1 校正公式

• 算法步骤

BFGS 算法

• 基本思想

• 性质

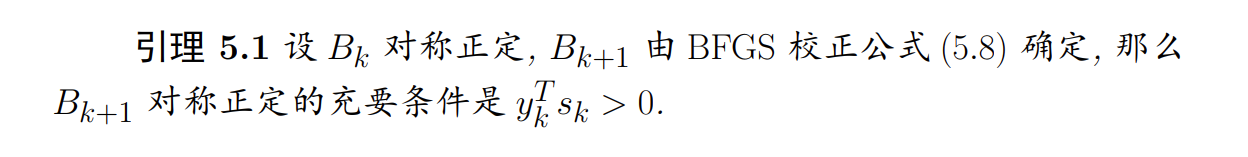
• 算法步骤

DFP 算法

• 基本思想

• 算法步骤

Broyden 族算法

• 性质

• 算法步骤

拟牛顿法的收敛性

• 超线性收敛的充分必要条件：

• BFGS 算法的局部超线性收敛定理：

最优性条件

等式约束问题的最优性条件

• 拉格朗日定理

• 二阶充分条件

不等式约束问题的最优性条件

• 非有效约束/有效约束

• 基础引理

  相容有点像向量的相关性，即a可以由b_i表示

  这里的

  

• KT 条件

一般约束问题的最优性条件

• KT 一阶必要条件

罚函数法

首先介绍求解约束优化问题的经典算法——罚函数法。其基本思想是：根据约束条件的特点将其转化为某种惩罚函数加到目标函数中去，从而将约束优化问题转化为一系列的无约束优化问题来求解。本章主要介绍外罚函数法、内点法和乘子法

外罚函数法

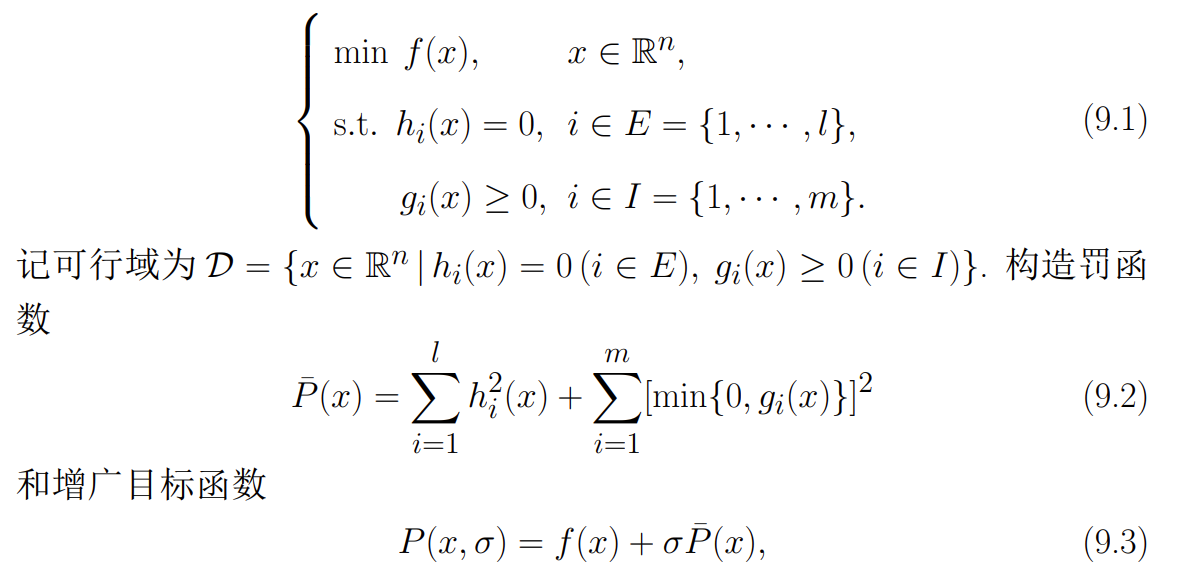
Note

常用的外罚函数有取平方、取绝对值等 需要注意的是${\sigma }_k$是一个很大的值，用来控制惩罚，从可行域外逐渐逼近可行域 优点：

• 外罚函数法结构简单，可以直接调用无约束优化算法的通用程序，因而容易编程实现 缺点：
• $x_k$ 往往不是可行点，这对于某些实际问题是难以接受的
• 罚参数 ${\sigma }_k$ 的选取比较困难，取的过小，可能起不到“惩罚”的作用，而取得过大则可能造成 $P(x,{\sigma }_k)$ 的 Hesse 阵的条件数很大，从而带来数值技术上的困难
• 注意到  $\overline{P}(x)$ 一般是不可微的, 因而难以直接使用利用导数的优化算法，从而收敛速度缓慢

内点法

Note

通常可以对函数取倒数之和作为罚函数 与外罚函数法相反，这里的$\tau$是一个很小的值，约束优化问题的极小点一般在可行域的边界上达到 优点： - 结构简单, 适应性强 缺点： - 随着迭代过程的进行，罚参数 ${\tau }_k$ 将变得越来越小，趋向于零，使得增广目标函数的病态性越来越严重 - 内点法的初始点 $x_0$ 要求是一个严格的可行点，一般来说这也是比较麻烦甚至困难的

乘子法

基本思想是从原问题的拉格朗日函数出发，再加上适当的罚函数，从而将原问题转化为求解一系列的无约束优化子问题。由于外罚函数法中的罚参数 ${\sigma }_k\to +\infty$，因此增广目标函数变得“越来越病态”。增广目标函数的这种病态性质是外罚函数法的主要缺点，而这种缺陷在乘子法中由于引入拉格朗日函数及加上适当的罚函数而得以有效的克服