部分参考资料:
- GNN 介绍 Blog,以下两个视频都参考了该博客
- 零基础多图详解图神经网络(GNN/GCN)【论文精读】_哔哩哔哩_bilibili
- 【唐博士带你学 AI】2022 最新图神经网络课程,同济大佬 53 集带你吃透 GNN,简直不要太透彻!
GNN 原理
图的结构
图的基本模块
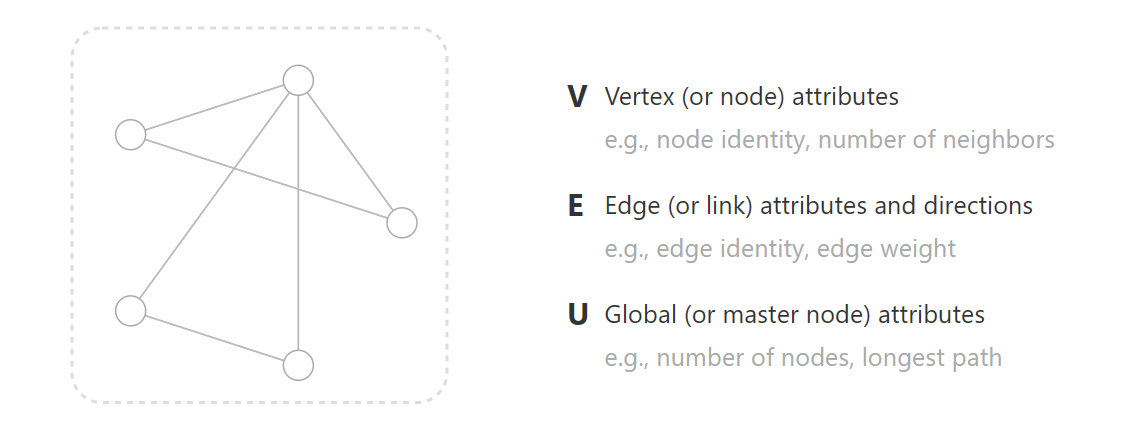 一个图由 V(顶点)、E(边)、U(全局变量)三个部分组成
一个图由 V(顶点)、E(边)、U(全局变量)三个部分组成
图的表示方法
- 邻接矩阵
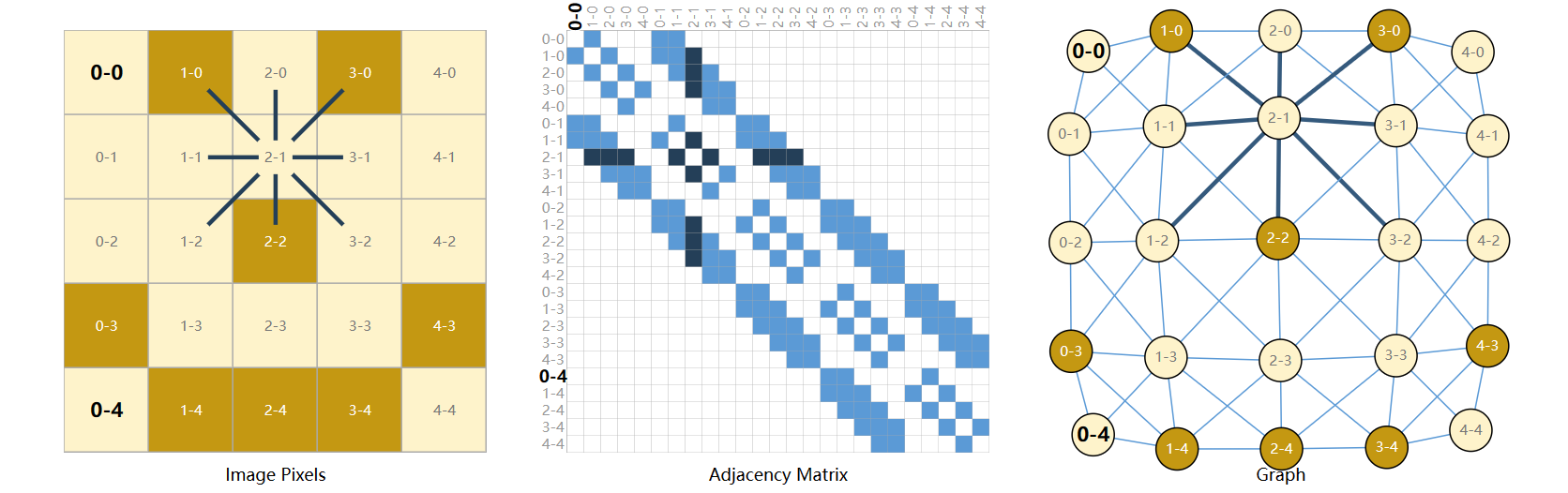 邻接矩阵是一个比较完整的例子,它包含了每一个节点之间的连接情况
缺点:
邻接矩阵是一个比较完整的例子,它包含了每一个节点之间的连接情况
缺点:
- 如果处理一个很大的稀疏矩阵,在 GPU 上的运算效率低
- 如果矩阵中元素的顺序改变了,图的结构也会发生很大变化
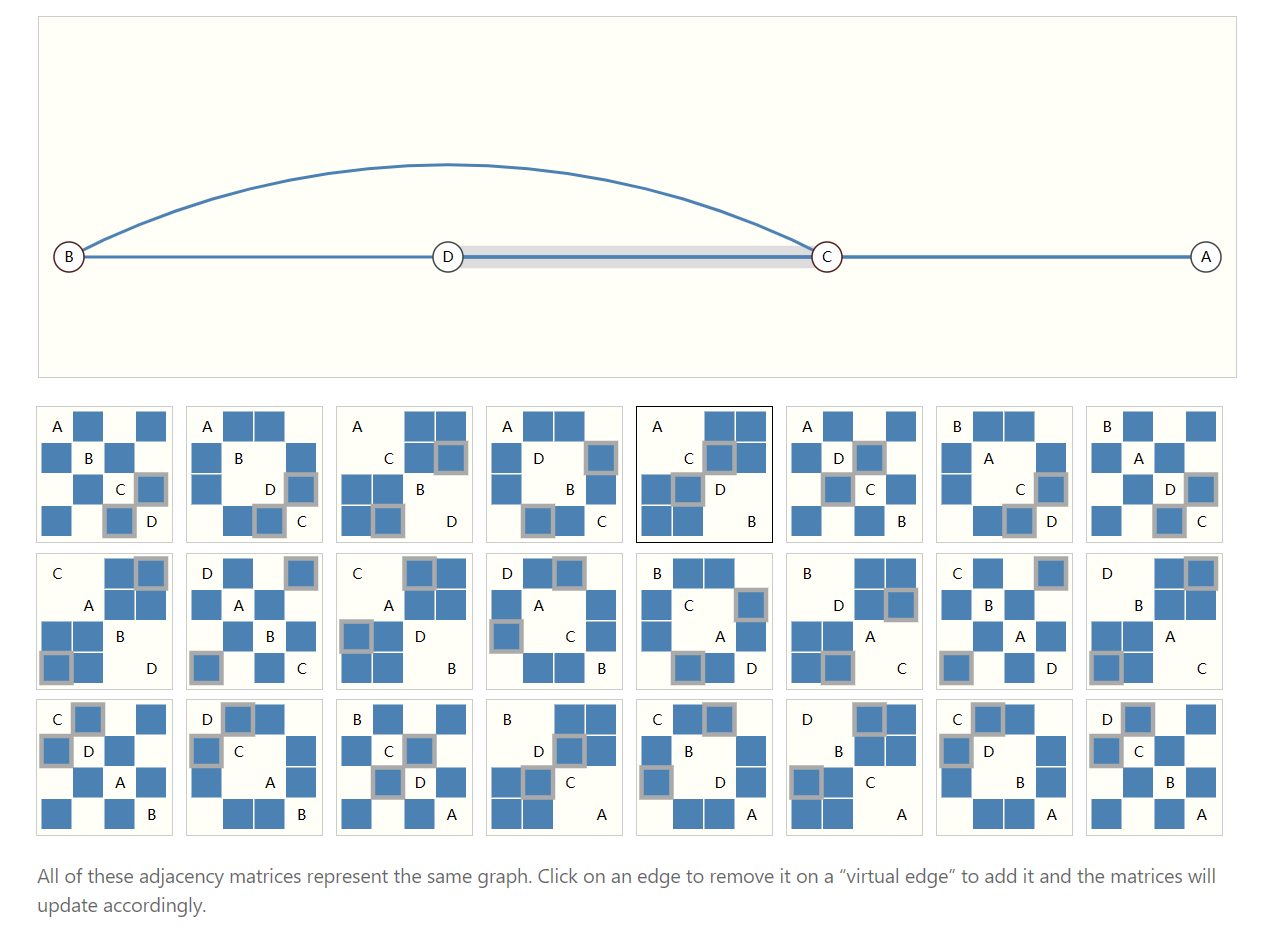
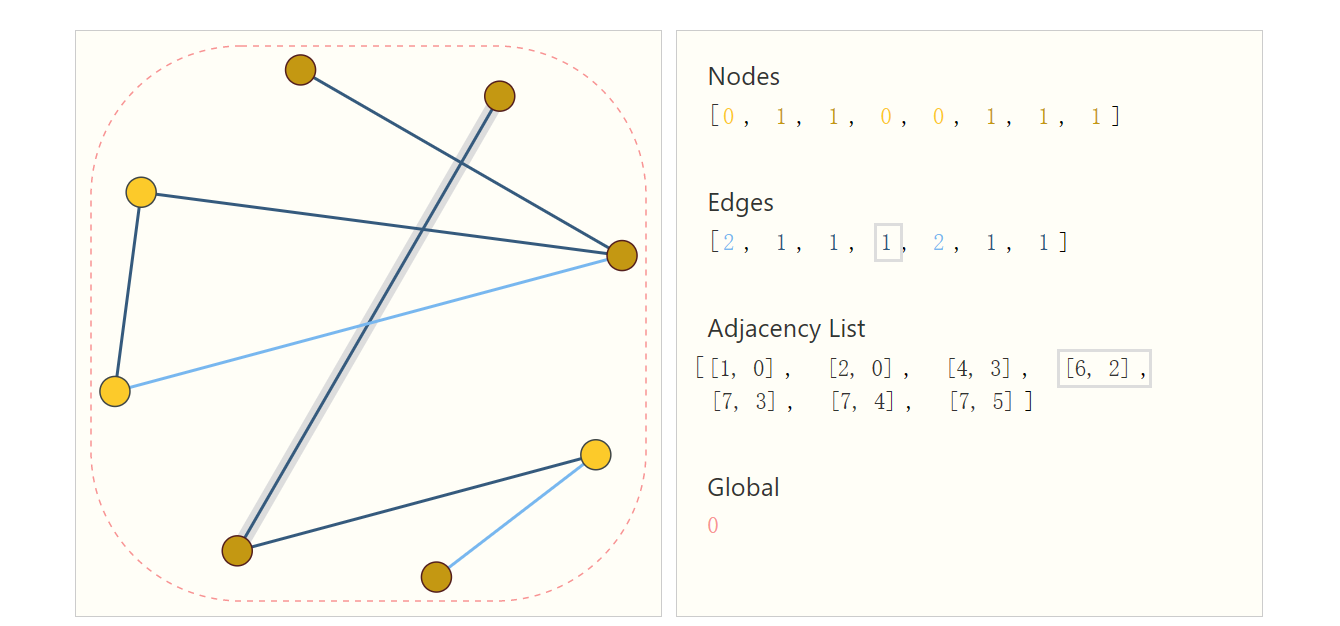
- 邻接列表
为了改进上面的问题,提出了使用邻接列表的方式来存储图信息:
MPNN(消息传递神经网络)
特征更新
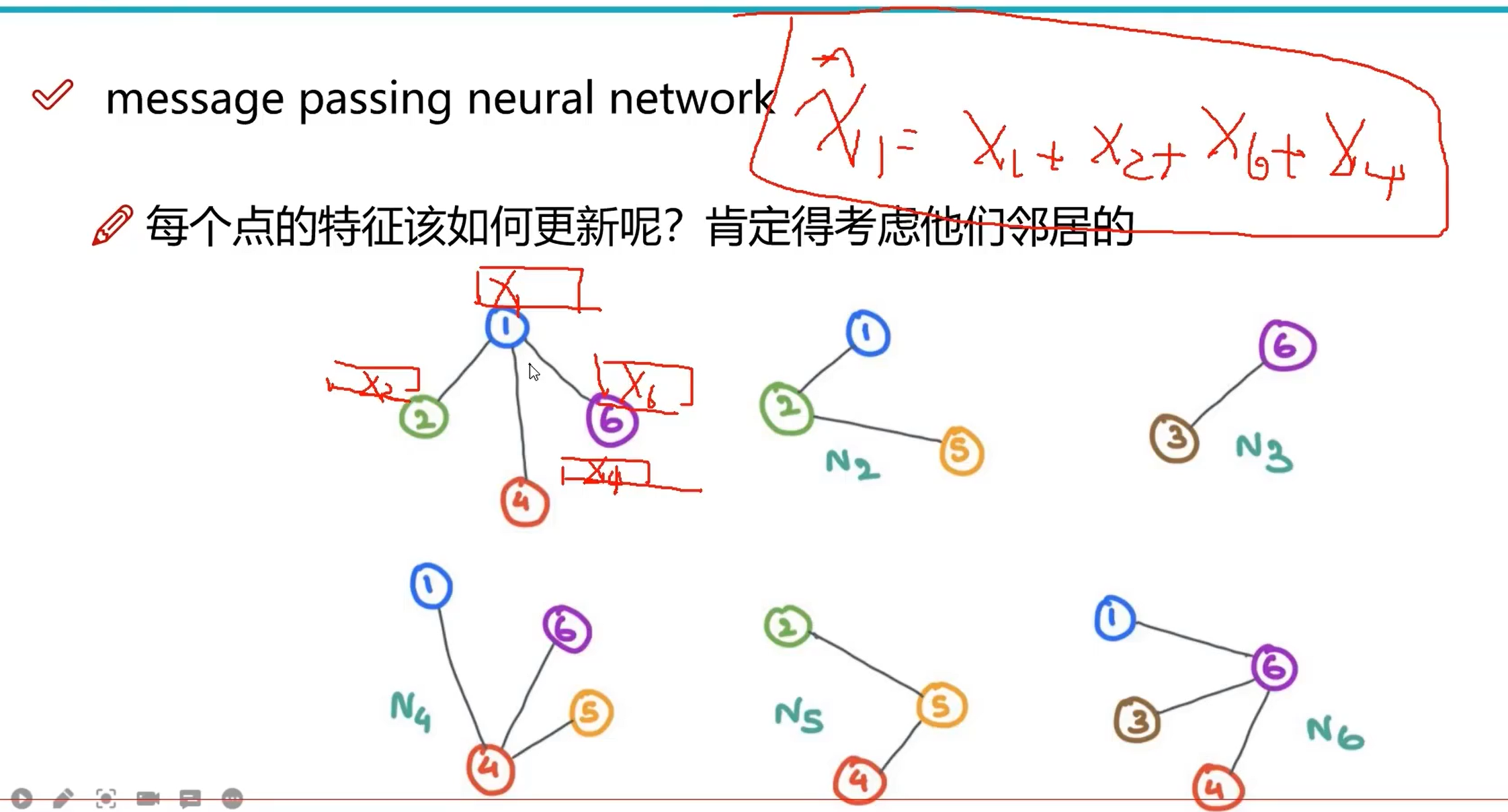 在 GNN 中,每个节点的更新需要考虑其相邻特征,假如现在有一个点 ,则它更新后为 ,当然,在真正的计算中并不是直接相加,而是带权重的
在 GNN 中,每个节点的更新需要考虑其相邻特征,假如现在有一个点 ,则它更新后为 ,当然,在真正的计算中并不是直接相加,而是带权重的
计算方法
具体的做法如下:
 在图神经网络中,除了 U、V、E 外,我们还需要对位置信息进行学习,因此需要利用消息传递机制,将相邻节点/边的信息给汇聚(pooling)起来
step1-生成权重 : 每个边都有一个可更新权重 ,在图中为
step2-pooling : 如果对某一个节点进行 ,则将相邻的节点 与该节点的特征一起参与计算,得到 后的特征,也就是图中的公式:
注:其中 可以替换为如上图右边所示的几种方法
在图神经网络中,除了 U、V、E 外,我们还需要对位置信息进行学习,因此需要利用消息传递机制,将相邻节点/边的信息给汇聚(pooling)起来
step1-生成权重 : 每个边都有一个可更新权重 ,在图中为
step2-pooling : 如果对某一个节点进行 ,则将相邻的节点 与该节点的特征一起参与计算,得到 后的特征,也就是图中的公式:
注:其中 可以替换为如上图右边所示的几种方法
多层 GNN
多层 GNN 的结构
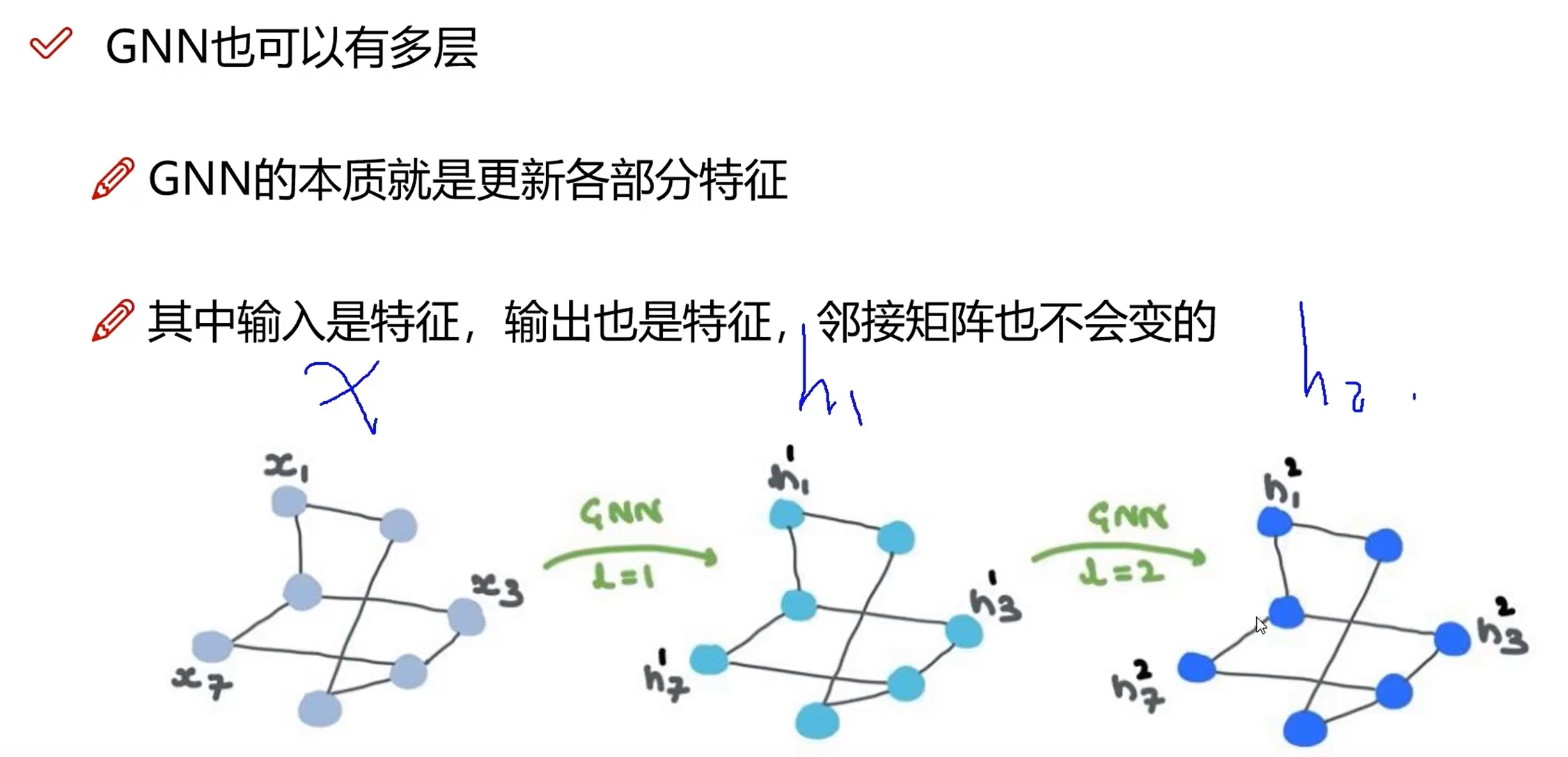 GNN 也可以像普通的神经网络一样叠多层,本质上讲就是更新权重,对于一个 GNN 来说,训练过程中图的连接是不会发生变化的
GNN 也可以像普通的神经网络一样叠多层,本质上讲就是更新权重,对于一个 GNN 来说,训练过程中图的连接是不会发生变化的
- 多层 GNN 的意义在哪呢? 多层 GNN 的特征更新会让每层的节点特征发生变化,每个节点会受到相邻节点的影响,通过多层 GNN 有利于获取全局信息(有点类似 CNN 中的感受野,越来越大… 最后一层可以获取全局信息)
Note
一开始的 GNN 在这里变成了 GCN(图卷积神经网络),其实内容上没有什么变化,GNN 是这一类的统称,,GCN 在 GNN 的基础上引入了消息传递机制,可以在多层 GCN 下获取整个图的信息
多层 GNN 的应用
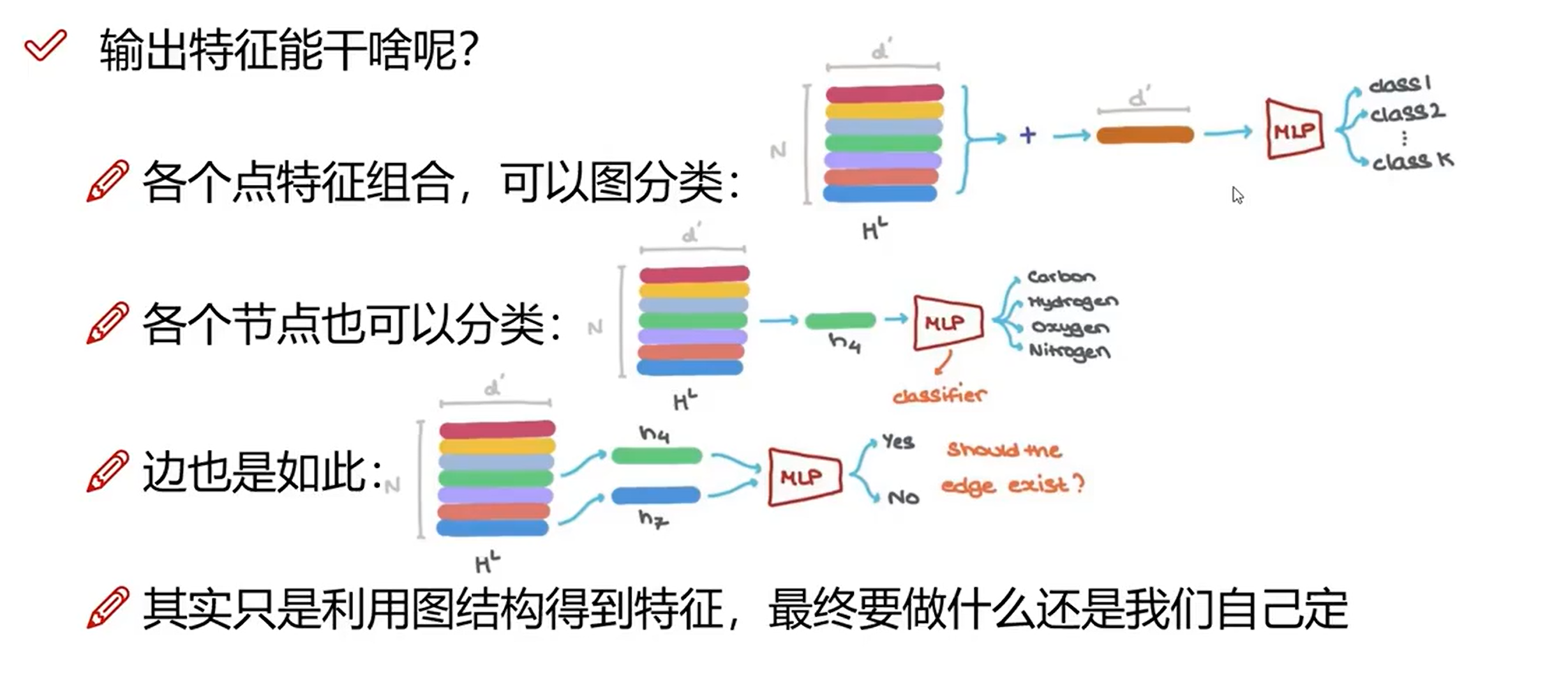 通过获取到点/边的信息,可以进行分类/回归等常见的机器学习任务,从上面的例子也可以看出,GNN 带来的主要是节点/边之间的关联信息,这种结构是传统的架构无法带来的
通过获取到点/边的信息,可以进行分类/回归等常见的机器学习任务,从上面的例子也可以看出,GNN 带来的主要是节点/边之间的关联信息,这种结构是传统的架构无法带来的
GCN
计算图
应用范围
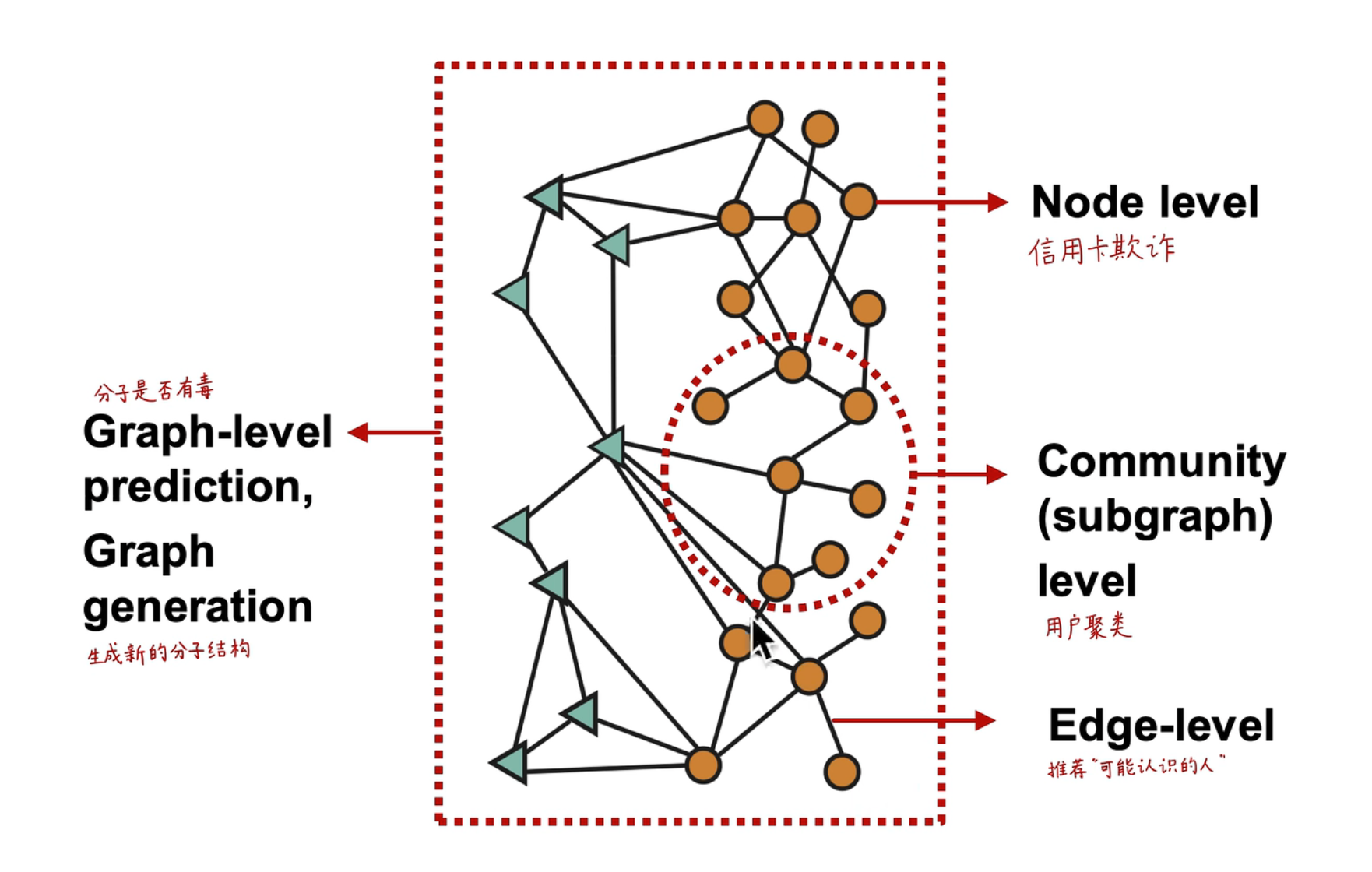 应用的范围主要分为几个层面:
应用的范围主要分为几个层面:
- 节点层面:判断是否可能存在信用卡欺诈
- 子图层面:对用户进行聚类
- 连接层面:两个节点直接是否会存在关联,在社交网络中应用较多
- 全图层面:判断分子是否有毒,或者能不能生成一个新的图
embedding 的重要性
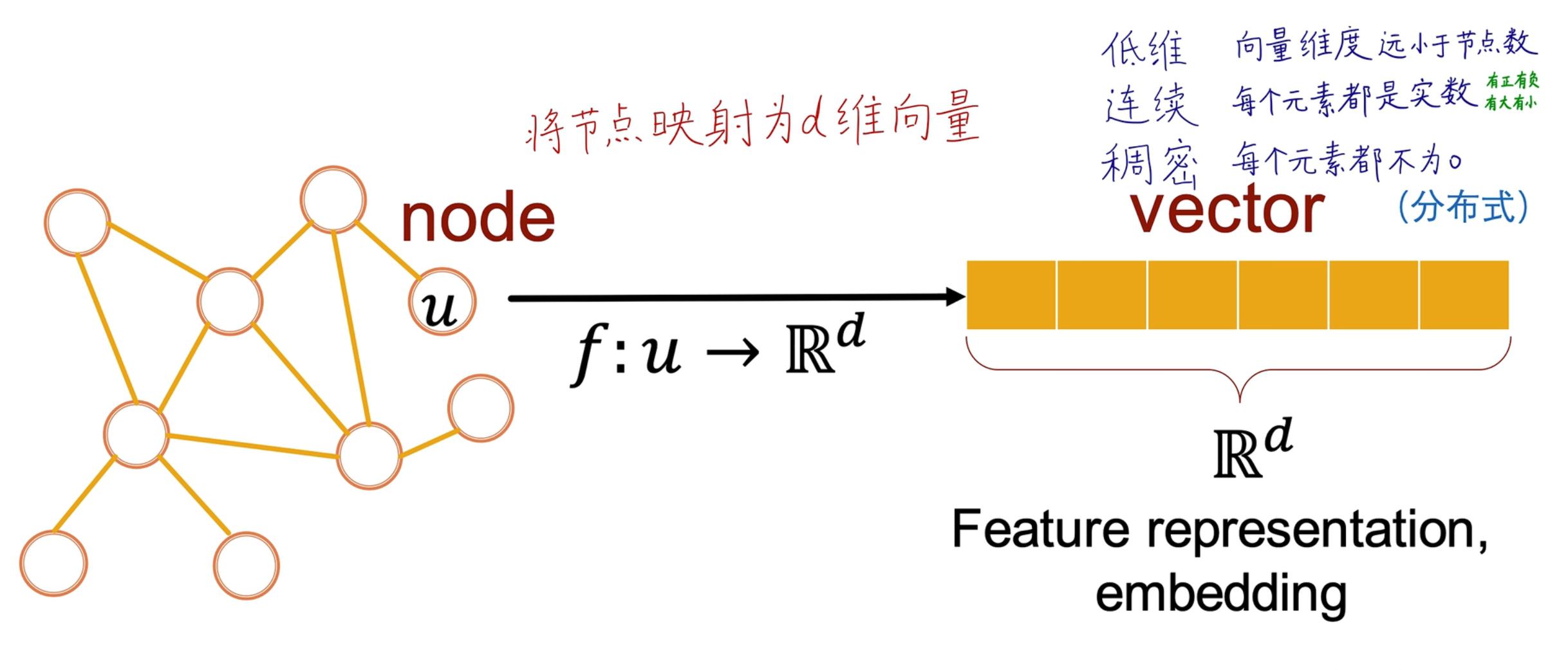
GNN 将节点映射为一个低维、连续、稠密的特征,这个向量就是一个图嵌入(embedding),在图中 d 维是人为设定的,这 d 维中包含了属性之间的连接关系、特征表示等等信息
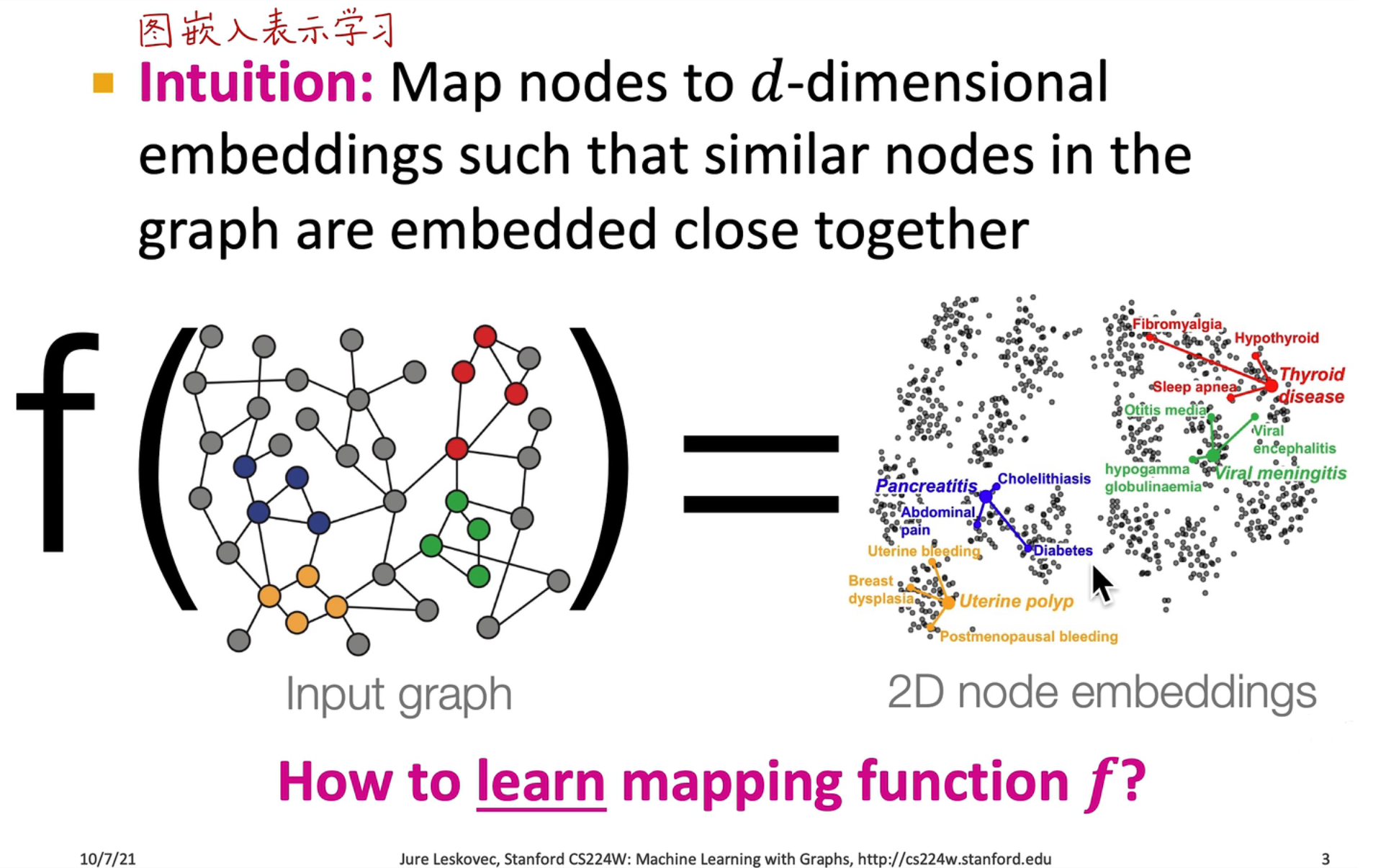 图神经网络相当于是对输入进行了一次 embedding 操作,从而获取到属性的关联关系,从而可以通过输出向量之间的距离,来反映原图的距离关系
图神经网络相当于是对输入进行了一次 embedding 操作,从而获取到属性的关联关系,从而可以通过输出向量之间的距离,来反映原图的距离关系
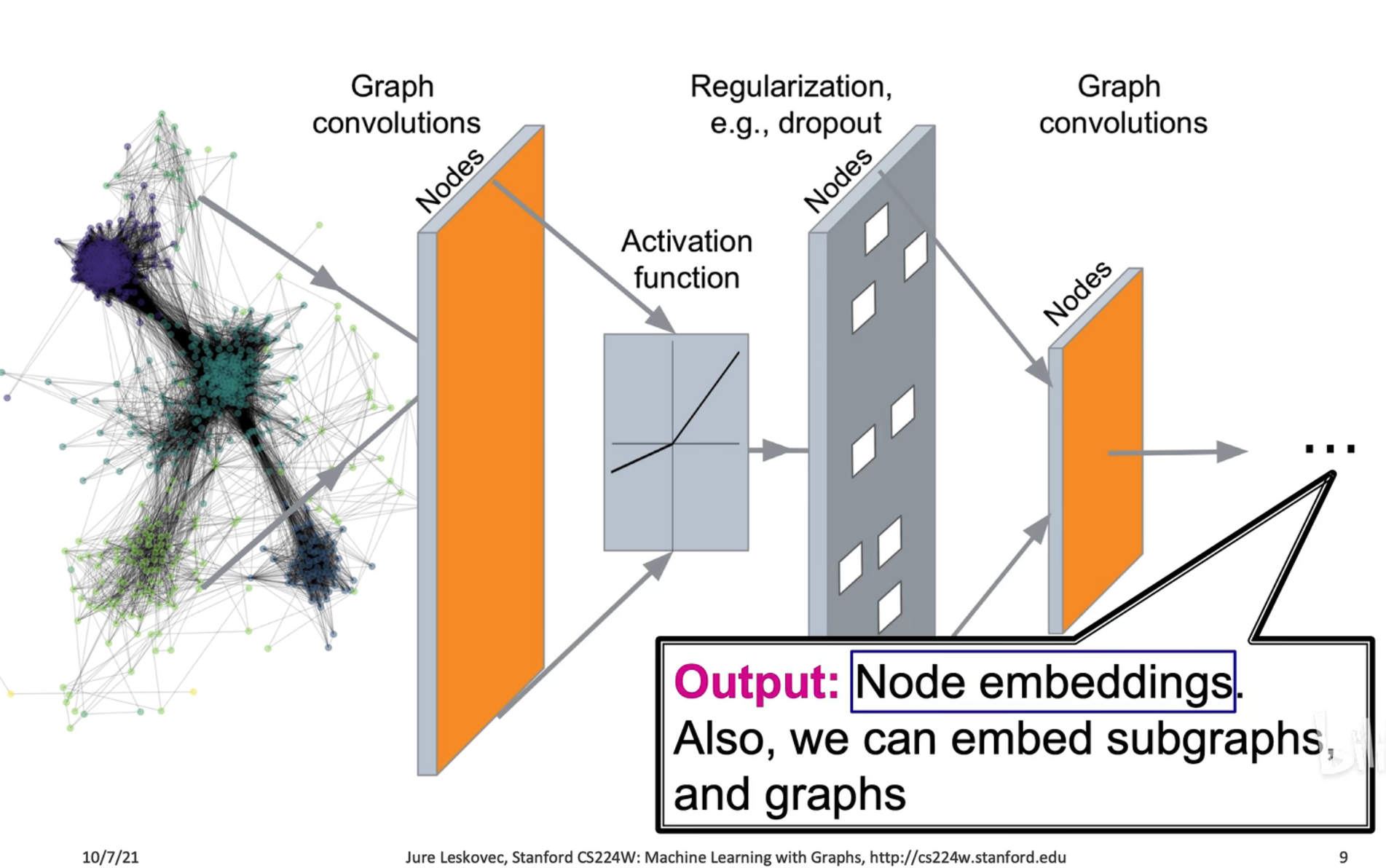 获得了节点的嵌入就可以添加最后一层,应用在上面的任务中,所以 embedding 的生成至关重要,我们需要生成一个质量足够高,足够反映节点和语义信息的 embedding 才能有比较好的效果
获得了节点的嵌入就可以添加最后一层,应用在上面的任务中,所以 embedding 的生成至关重要,我们需要生成一个质量足够高,足够反映节点和语义信息的 embedding 才能有比较好的效果
GNN 架构
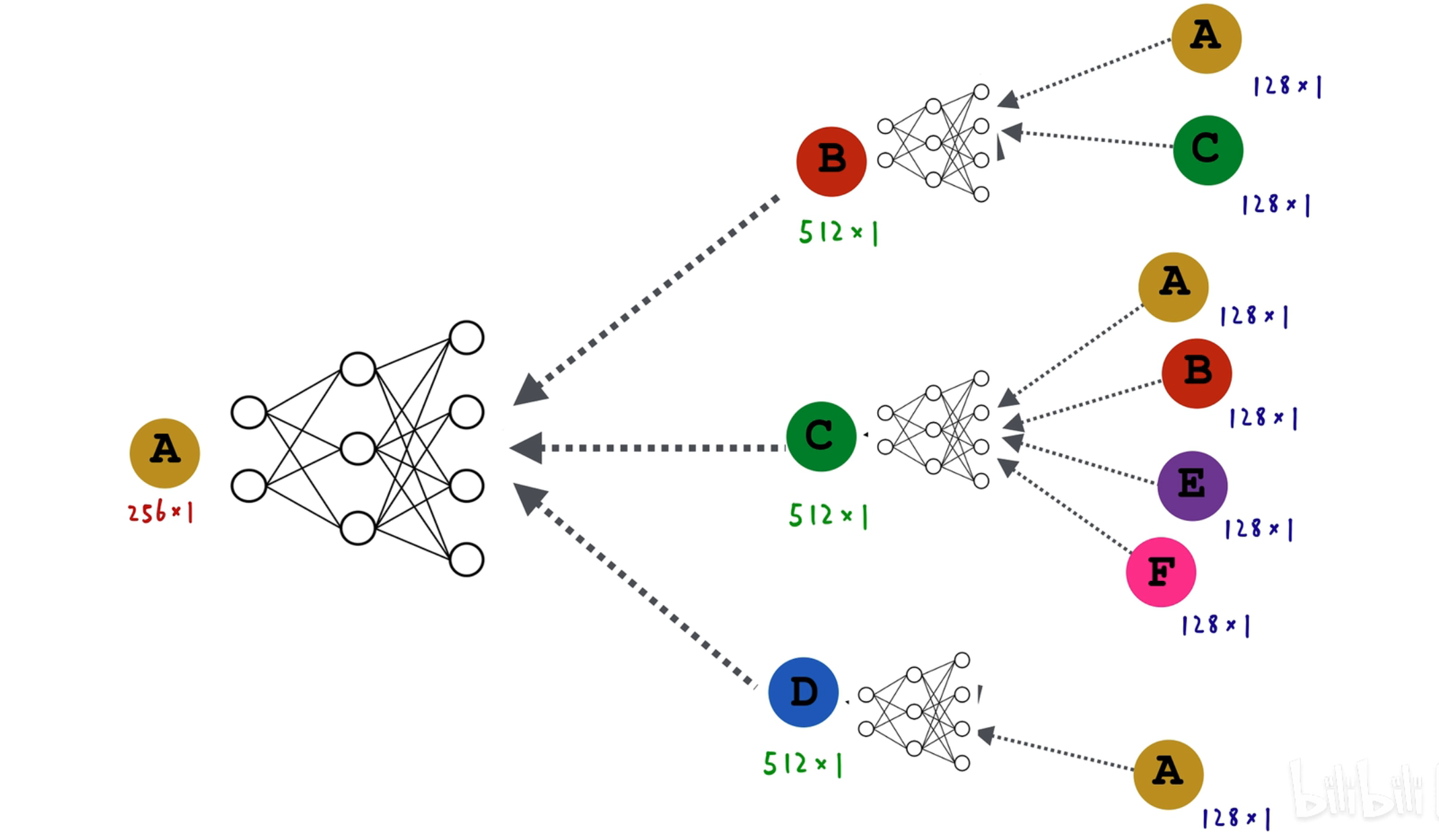
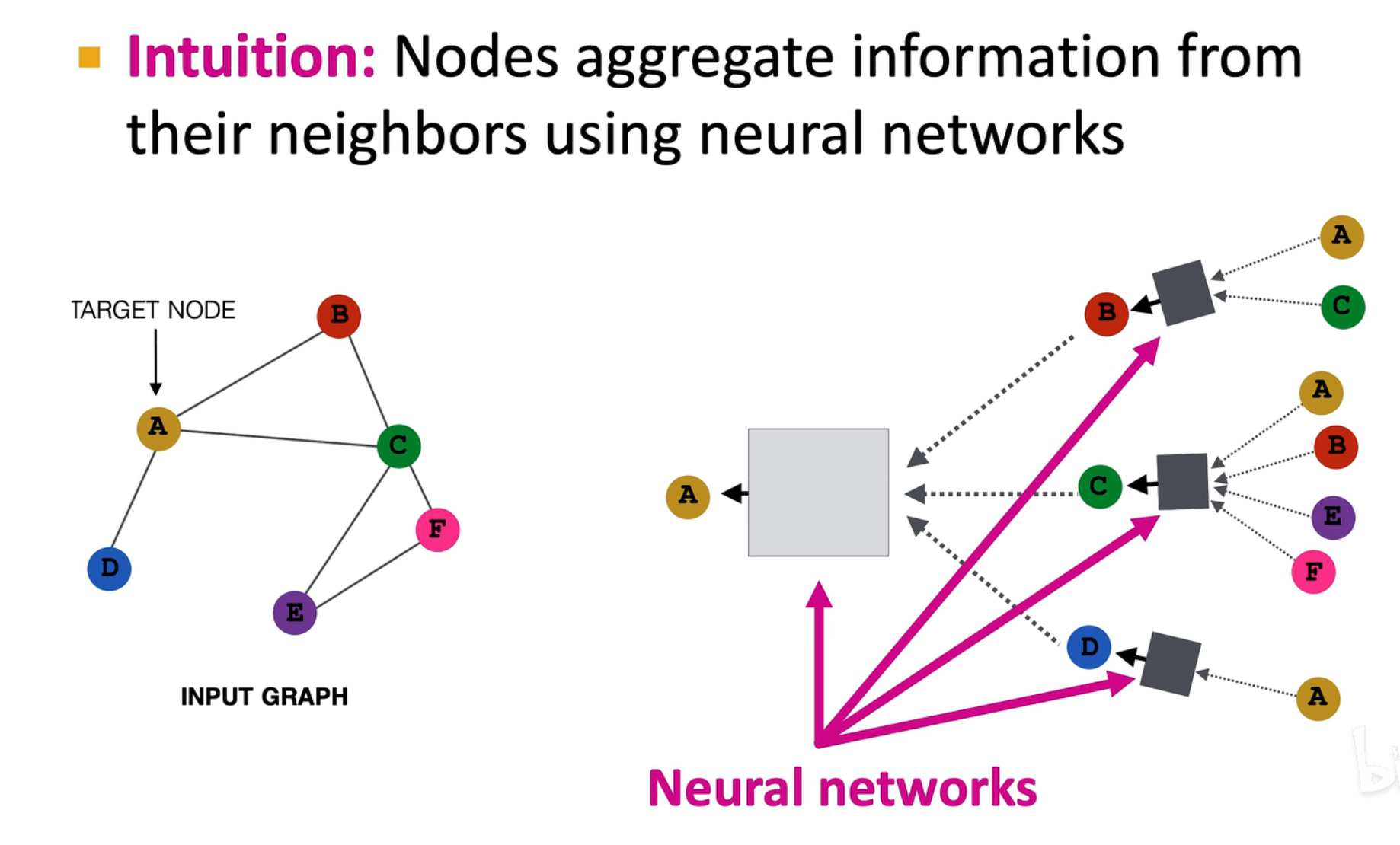 计算的关键是建立一个计算图,在图中方框表示一层 GCN,深色的方框表示第一层,灰色的方框表示第二层,颜色相同的层共享一套权重
计算的关键是建立一个计算图,在图中方框表示一层 GCN,深色的方框表示第一层,灰色的方框表示第二层,颜色相同的层共享一套权重
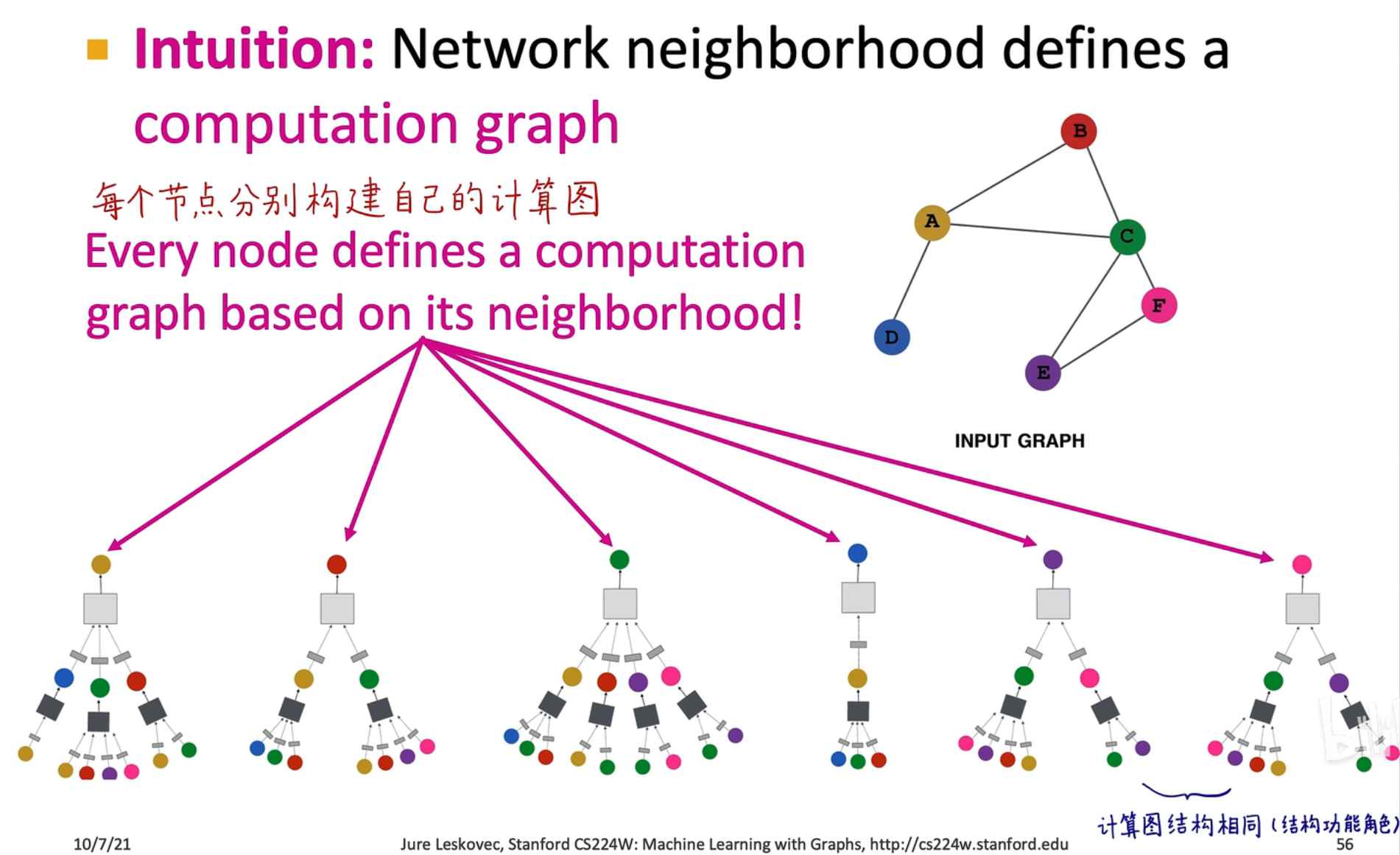 在训练过程中,每一个计算图就是一个样本,如上图所示就是
在训练过程中,每一个计算图就是一个样本,如上图所示就是 batch_size=6,这就是一步迭代的过程
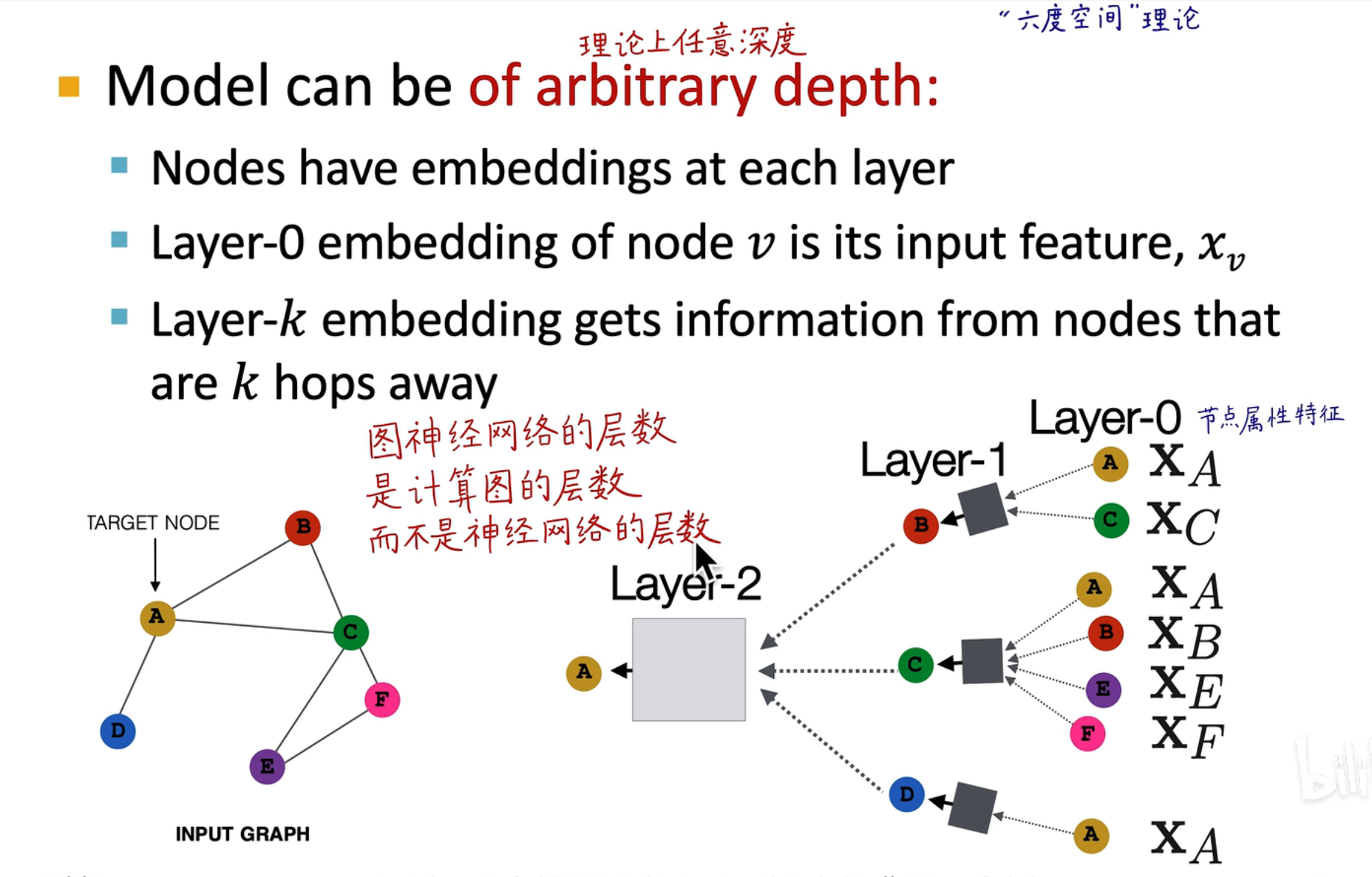 在 GNN 中需要搞清楚计算图的概念,不要和神经网络层数搞混淆:
在 GNN 中需要搞清楚计算图的概念,不要和神经网络层数搞混淆:
- 计算图:一般指图神经网络的层数,是在每个 batch 中需要计算的层数,如上图所示就是一个 2 层计算图的网络
- 神经网络层数:指的是每个计算图中可以添加的层数(即在方框内添加的层数),在这里可以变得很深,就像传统的神经网络架构一样
根据六度空间理论,通过简单的六层关系就可以认识全世界的人,因此我们的 GNN 层数不宜过深
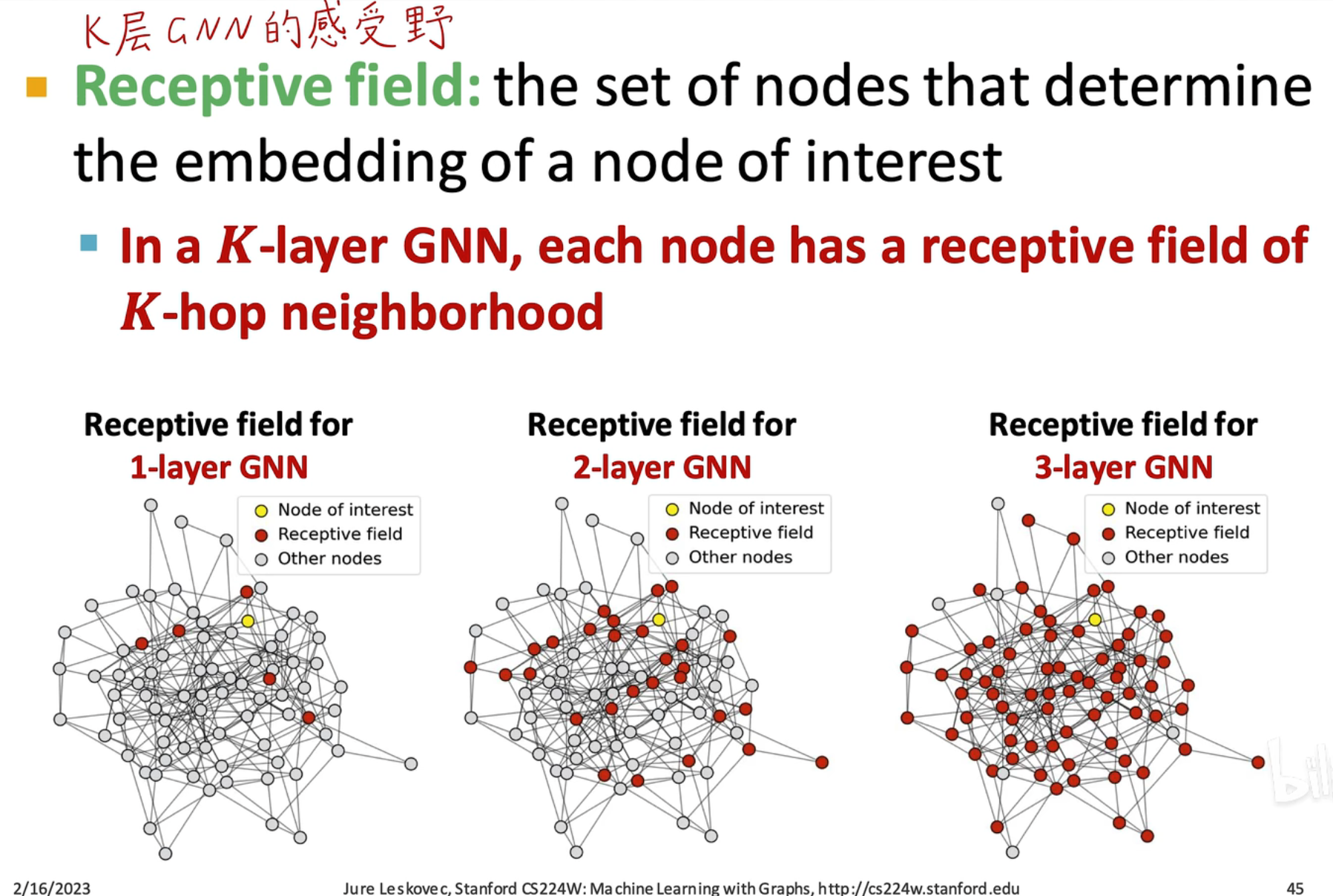 在 GNN 中,层数越多,感受野就会越大,如果 GNN 层数太深就会学习不到正常的属性关系,从而导致过平滑(over-smoothing)问题,即所有节点都收敛到同一个值,没学习到特征
在 GNN 中,层数越多,感受野就会越大,如果 GNN 层数太深就会学习不到正常的属性关系,从而导致过平滑(over-smoothing)问题,即所有节点都收敛到同一个值,没学习到特征
传播过程
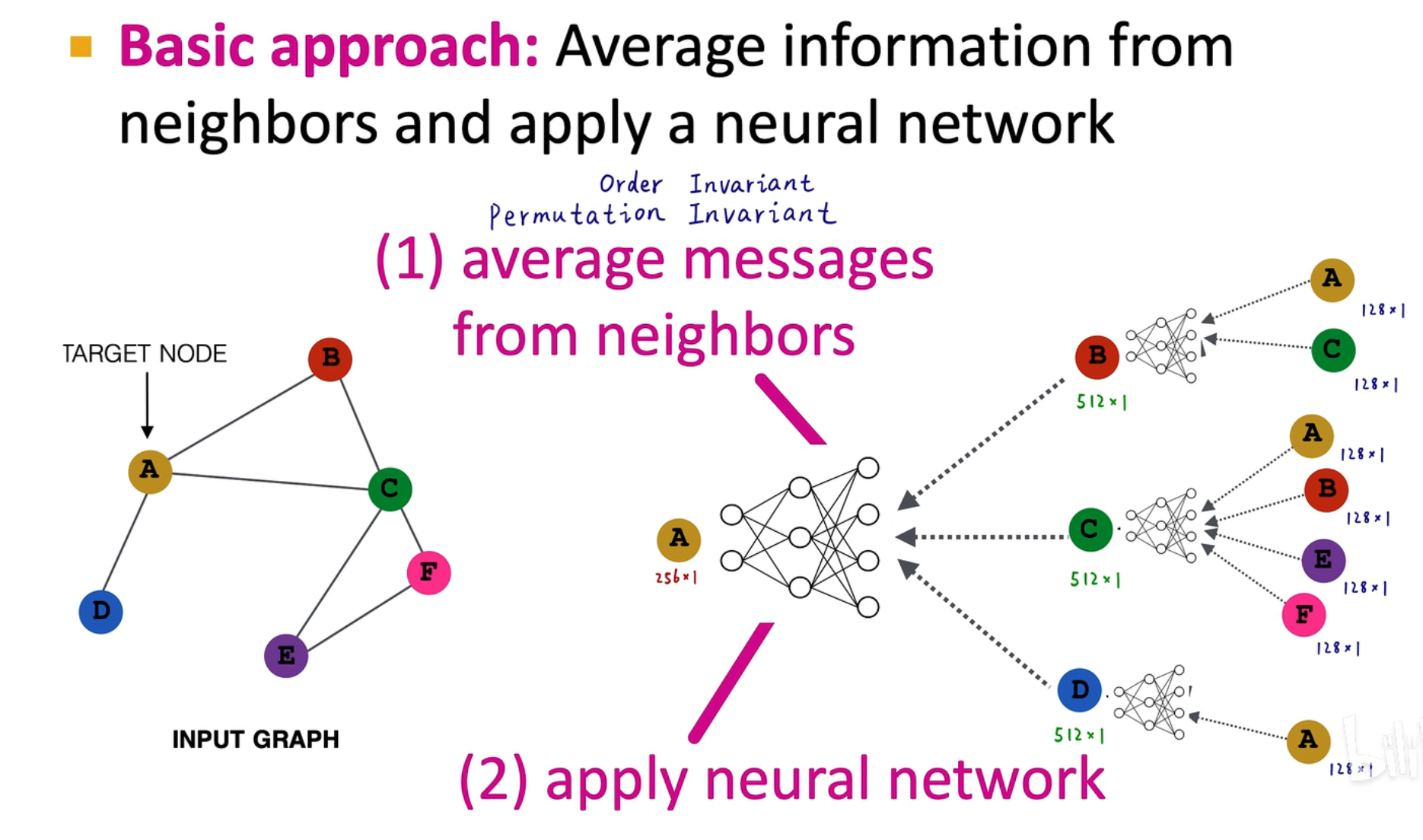 类似上述的 MPNN(消息传递神经网络) 的平均算法,中间 128 维到 512 维的转换过程可以通过一个 FNN 实现
类似上述的 MPNN(消息传递神经网络) 的平均算法,中间 128 维到 512 维的转换过程可以通过一个 FNN 实现
数学形式
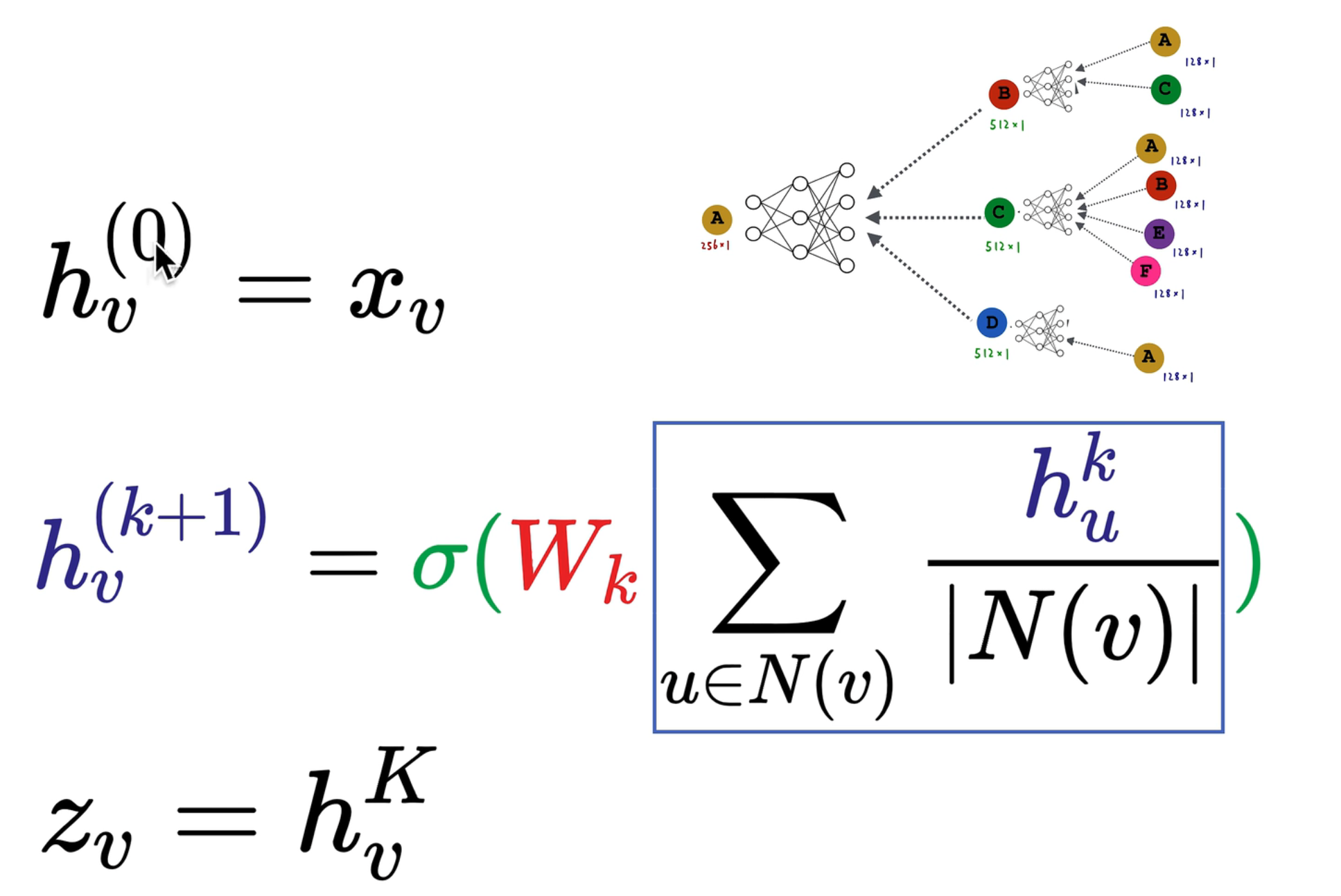
- 是第 层,就是对象的属性特征
- 是第 层,是由第 k 层的邻域节点 来计算的, 是神经网络的权重, 是激活函数
- 中的 表示计算图层数,例如在上图中,,我们直接把最后一层作为输出的 embedding
矩阵表示
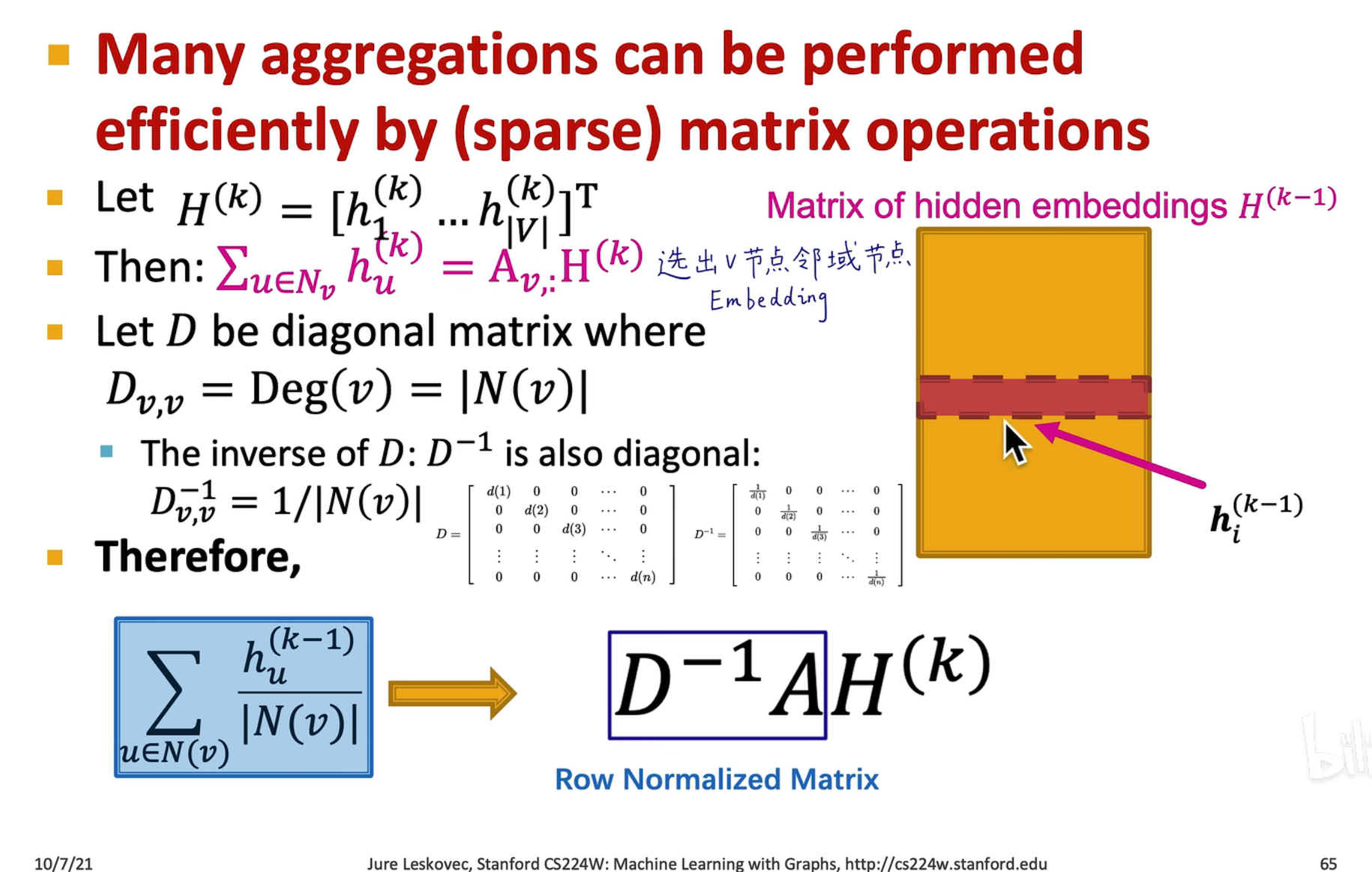
- 先把前一层的 embedding 用 表示,然后用 选出 节点的邻域节点(通过左乘邻接矩阵的第 行)
- 表示表示 v 节点的连接数, 矩阵就是一个对角矩阵,表示第 i 个节点的邻接节点数,因此最后的求和可以用矩阵表示为
Row Normalized Matrix
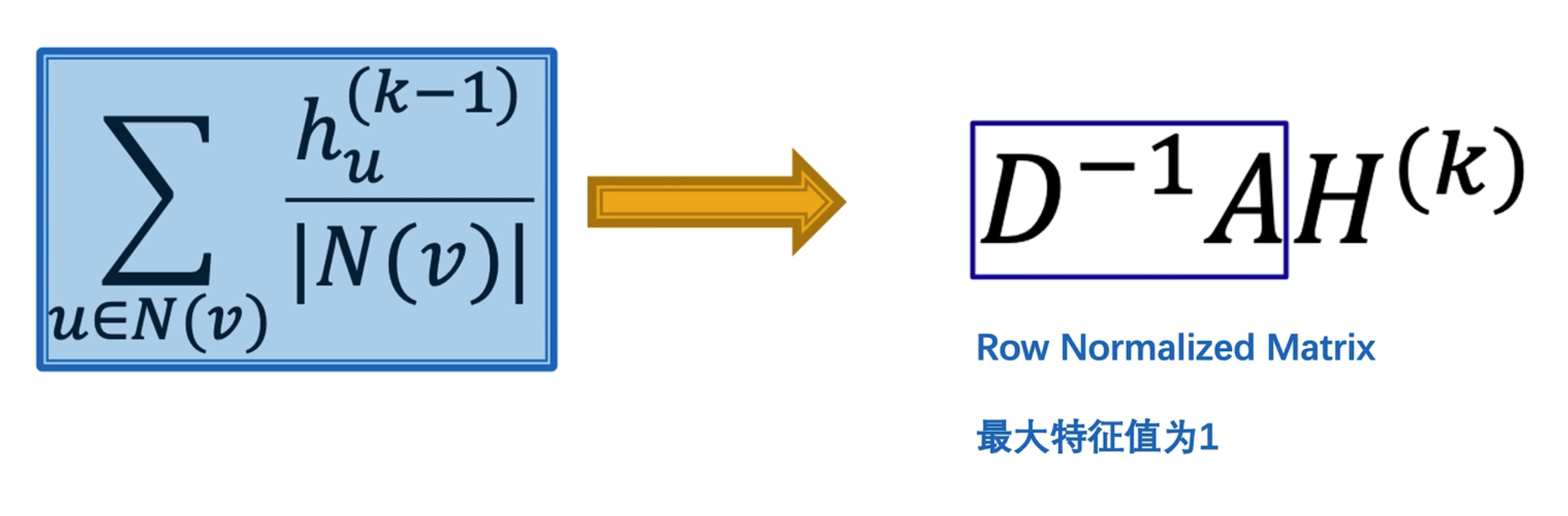 上图中的蓝框部分又叫做“行标准化矩阵”,最大的特征值为 1,为的就是筛选出邻域节点并做求平均操作
上图中的蓝框部分又叫做“行标准化矩阵”,最大的特征值为 1,为的就是筛选出邻域节点并做求平均操作
Bug
但这种 Row Normalized Matrix 只是简单平均,没有考虑到连接节点的邻域关系,因此我们需要进行改进!
Normalized Adjacency Matrix
改进 Row Normalized Matrix,如下图所示:
 对左右两边同乘 ,这样可以在考虑邻域关系的情况下,尽可能减少幅值的影响
对左右两边同乘 ,这样可以在考虑邻域关系的情况下,尽可能减少幅值的影响
Important
如果左右都乘 ,则特征值范围在 ,尽可能减少幅值的影响(个人理解:可能会降低网络的表达能力,不能还原出大小不变,方向不变的特征)
Intuitive reason
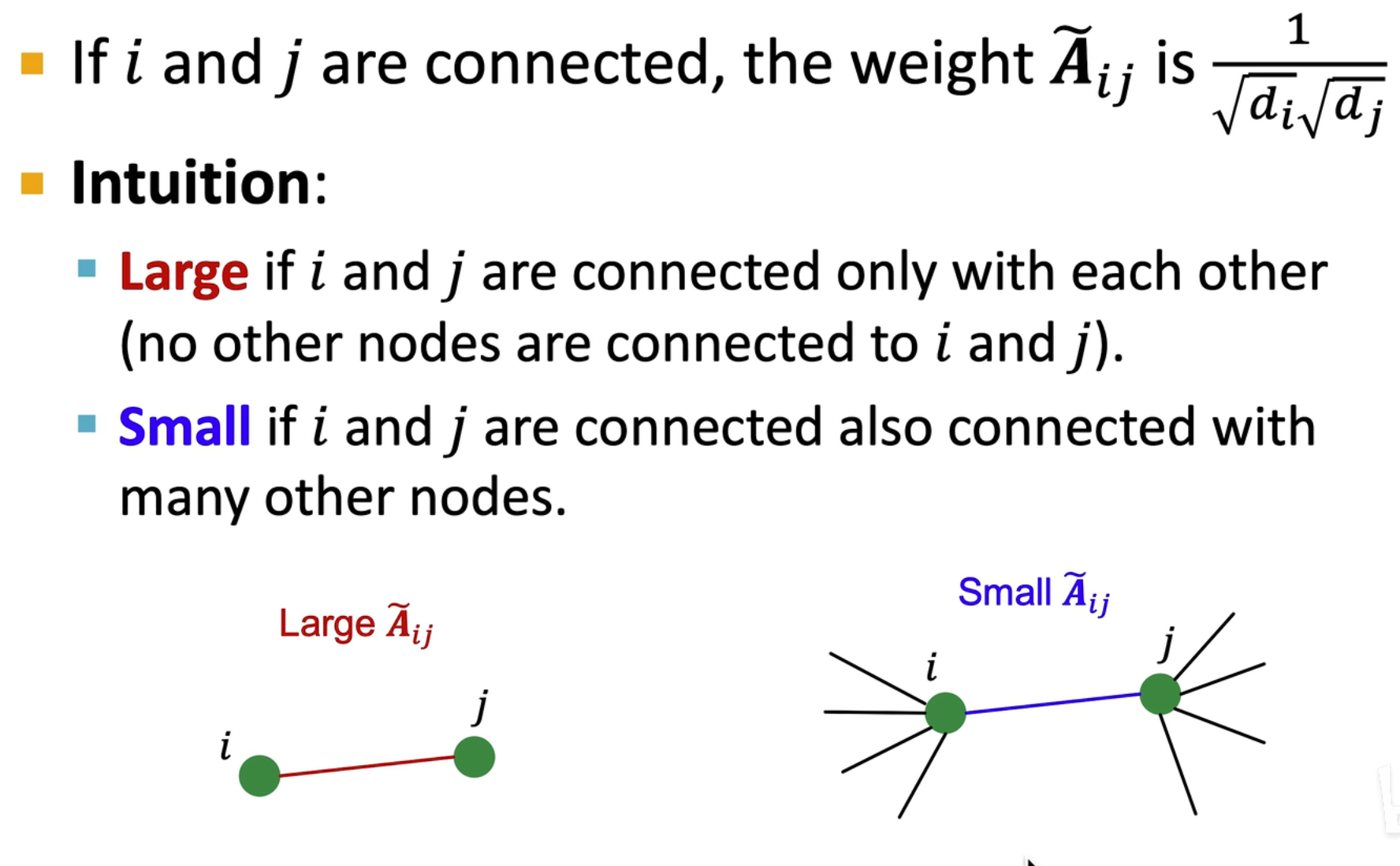 因为其最大特征值也为 1,因此有很好的性质,同时从直观角度上讲,采用这种方式会给单独连接赋予更高的权重,对多个连接的减少它的权重
因为其最大特征值也为 1,因此有很好的性质,同时从直观角度上讲,采用这种方式会给单独连接赋予更高的权重,对多个连接的减少它的权重
Mathematical derivation
 其特征值在 ,并且最大特征值始终为 1,这里给出了证明,对于向量 ,如果特征值为 1,则特征向量为
其特征值在 ,并且最大特征值始终为 1,这里给出了证明,对于向量 ,如果特征值为 1,则特征向量为
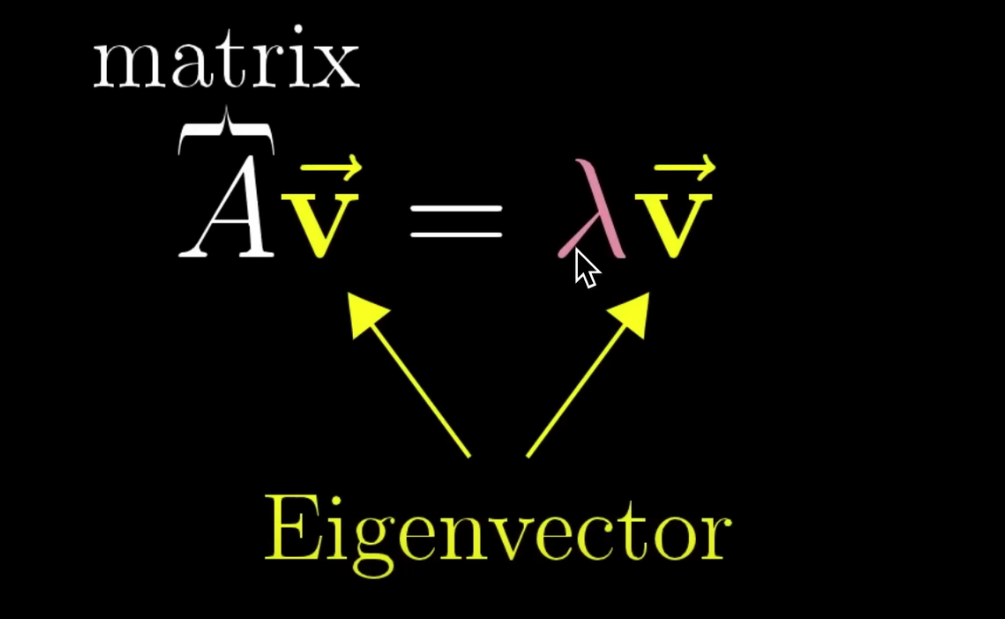 这样的好处是,对于向量 来说,可以反复左乘 和特征值,能够保证幅值不变
在矩阵表示中的 就相当于这个式子中的 ,左乘的 就相当于这里的 (行标准化矩阵),这样可以保证 幅值不变
这样的好处是,对于向量 来说,可以反复左乘 和特征值,能够保证幅值不变
在矩阵表示中的 就相当于这个式子中的 ,左乘的 就相当于这里的 (行标准化矩阵),这样可以保证 幅值不变
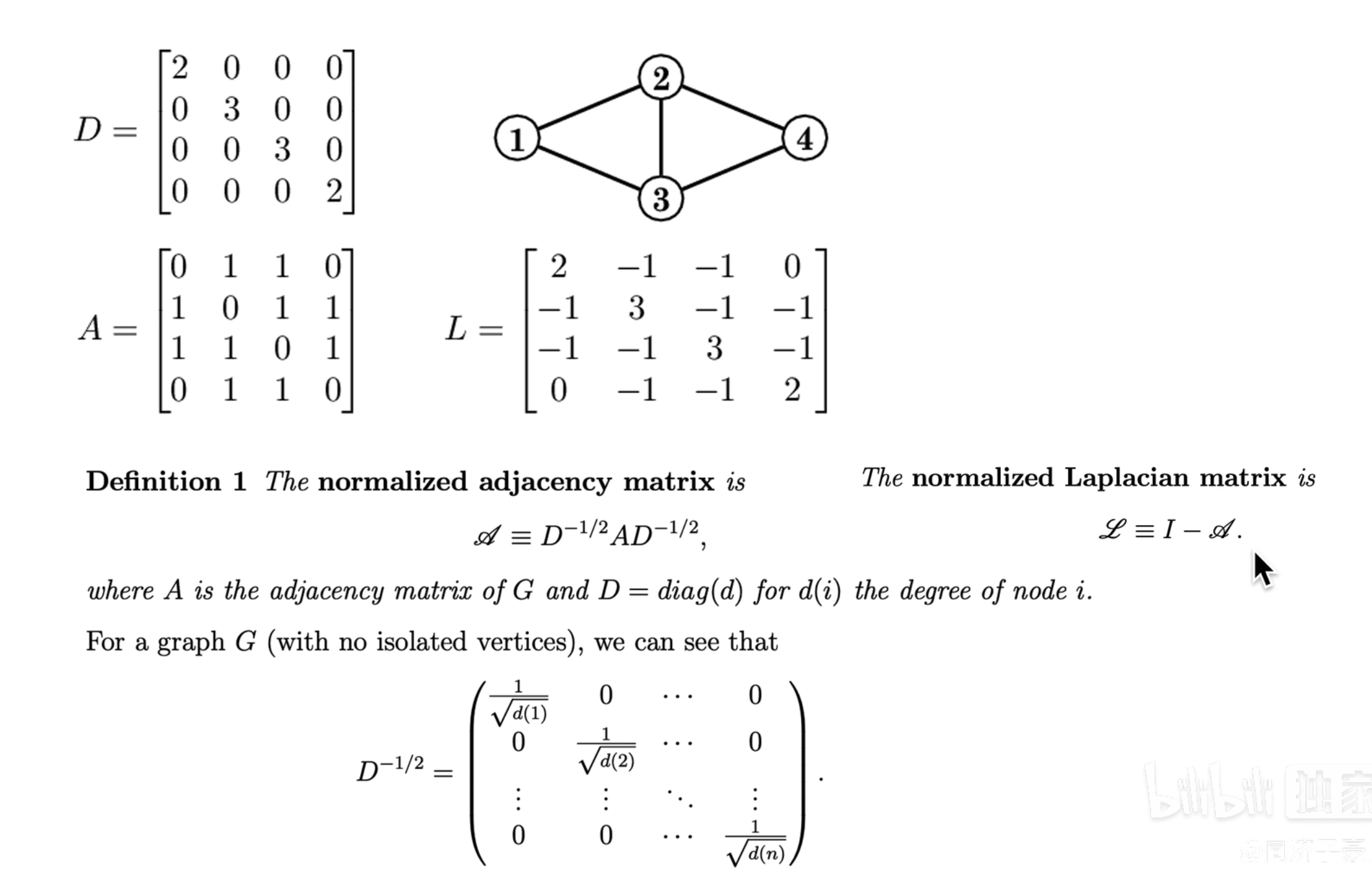 这是从空域的角度来解释 GCN,当然还可以从时域和频域的拉普拉斯变换的角度理解
这是从空域的角度来解释 GCN,当然还可以从时域和频域的拉普拉斯变换的角度理解
Summary
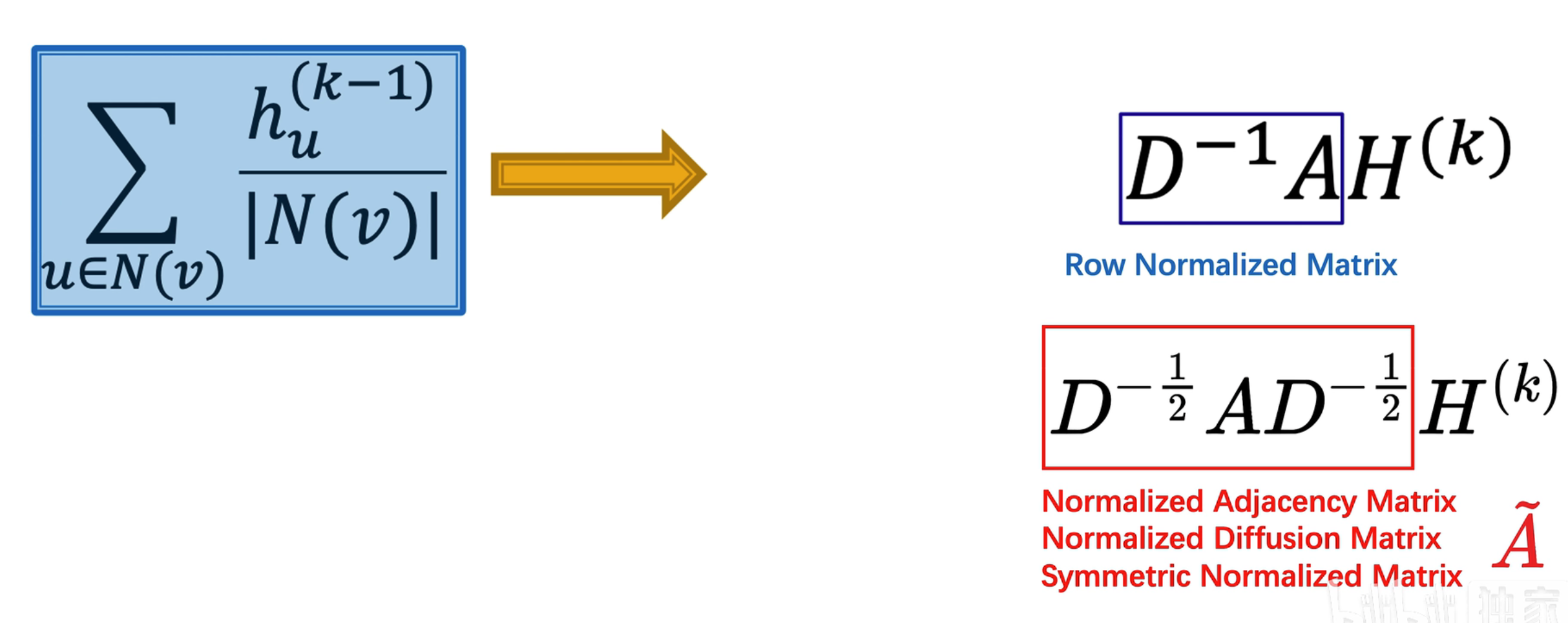 从 Row Normalized Matrix 到 Normalized diffusion Matrix 是一个重要的变换过程,在变换后可以得到许多有用的性质,同时考虑了两个节点之间的连接情况
从 Row Normalized Matrix 到 Normalized diffusion Matrix 是一个重要的变换过程,在变换后可以得到许多有用的性质,同时考虑了两个节点之间的连接情况
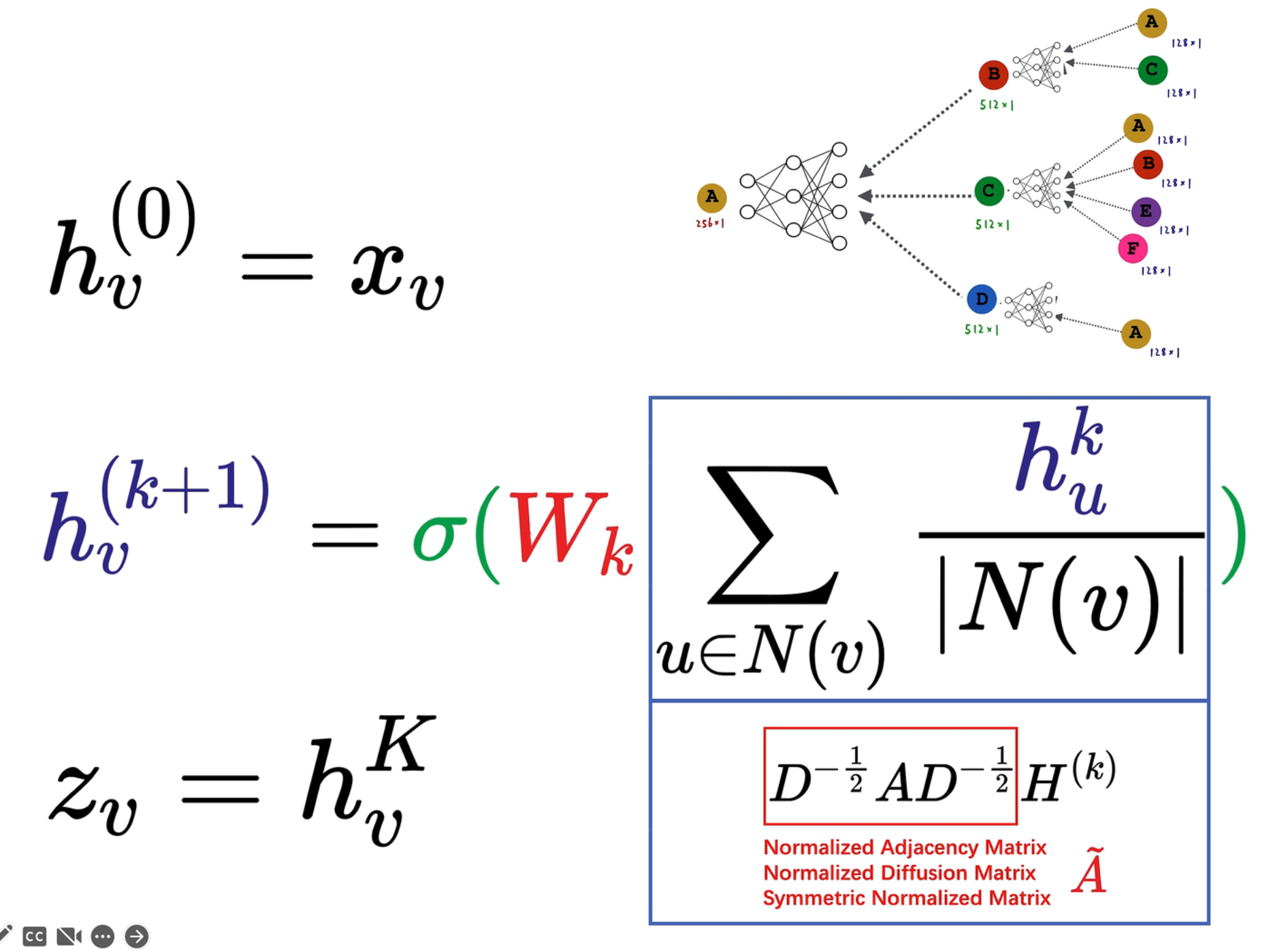 最后的公式形式如图所示,就是 GCN 论文中提到的公式
最后的公式形式如图所示,就是 GCN 论文中提到的公式
计算图的改进
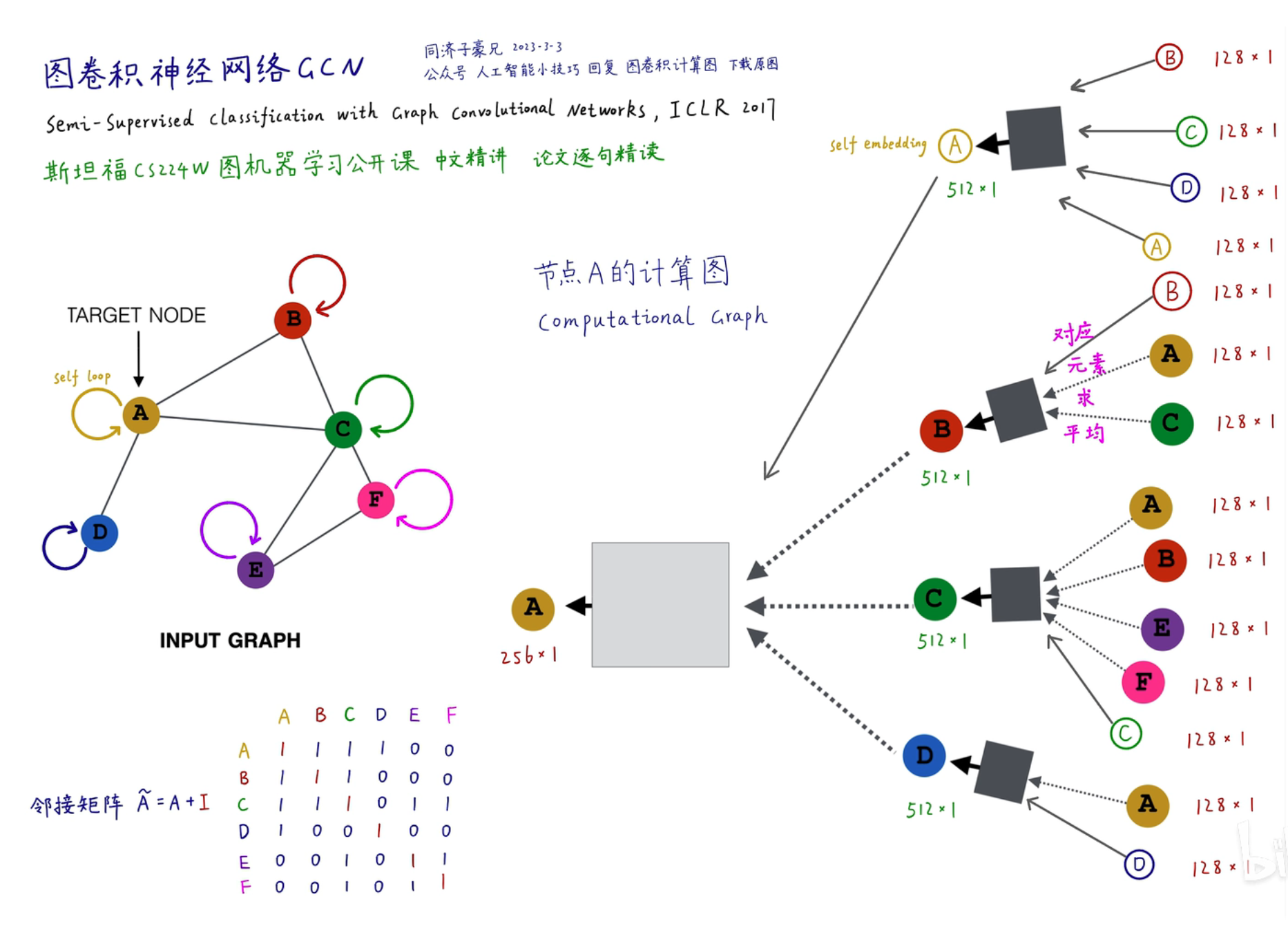
- 计算图存在的问题:节点本身没有考虑到,因此会导致图忽略了节点自身的特征向量
- 改进方法:将邻接矩阵改为 ,其中 是单位阵,这样每次在计算图中就会考虑其自身的特征向量
 因此最后的公式可以写成成 4.6 和 4.7 两种形式,
4.6 中是将自身的特征和其它特征放在一起考虑,进行平均求和
4.7 中把其它特征和自身特征分开,然后相加, 是第 个节点的邻域数量
因此最后的公式可以写成成 4.6 和 4.7 两种形式,
4.6 中是将自身的特征和其它特征放在一起考虑,进行平均求和
4.7 中把其它特征和自身特征分开,然后相加, 是第 个节点的邻域数量
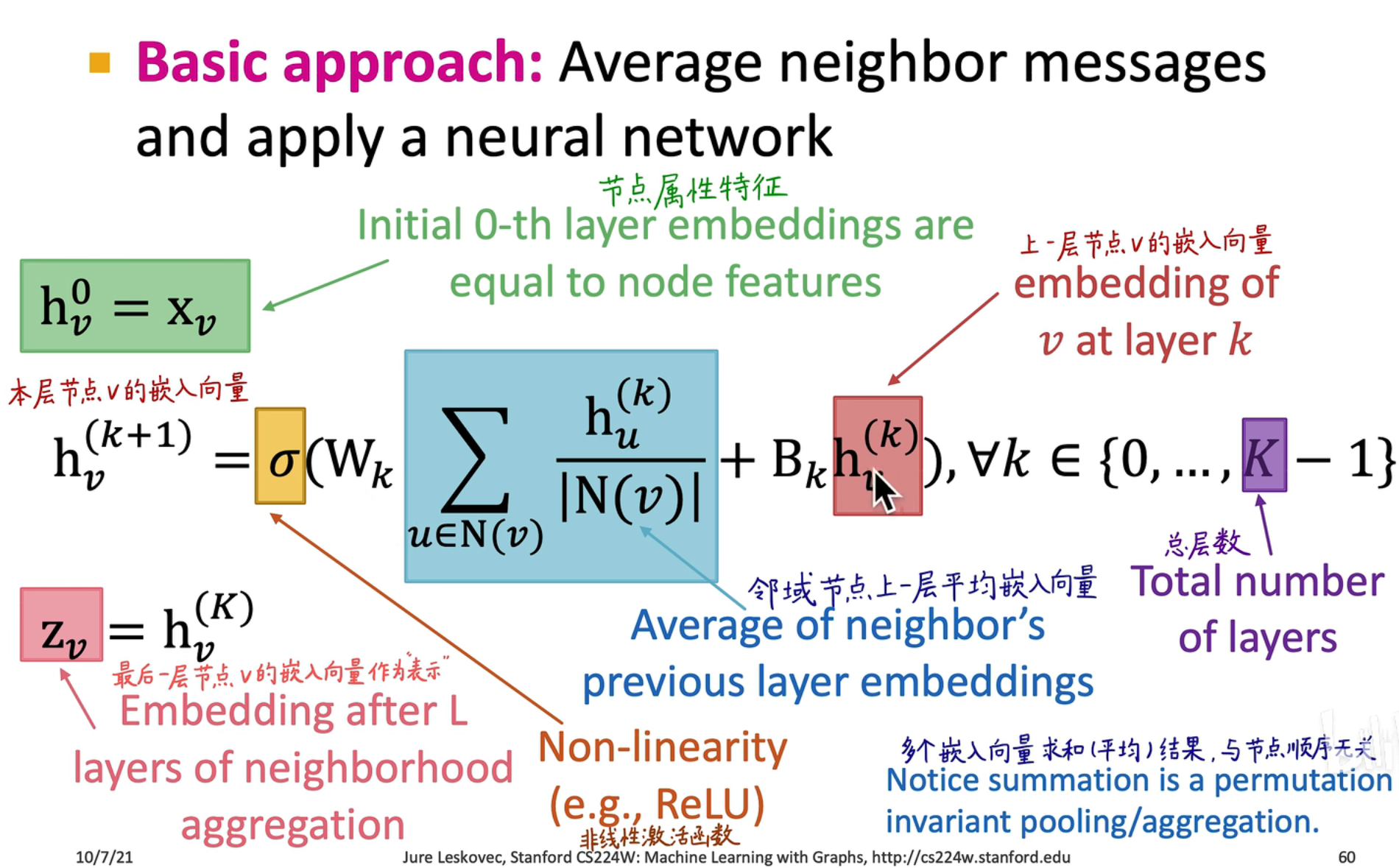
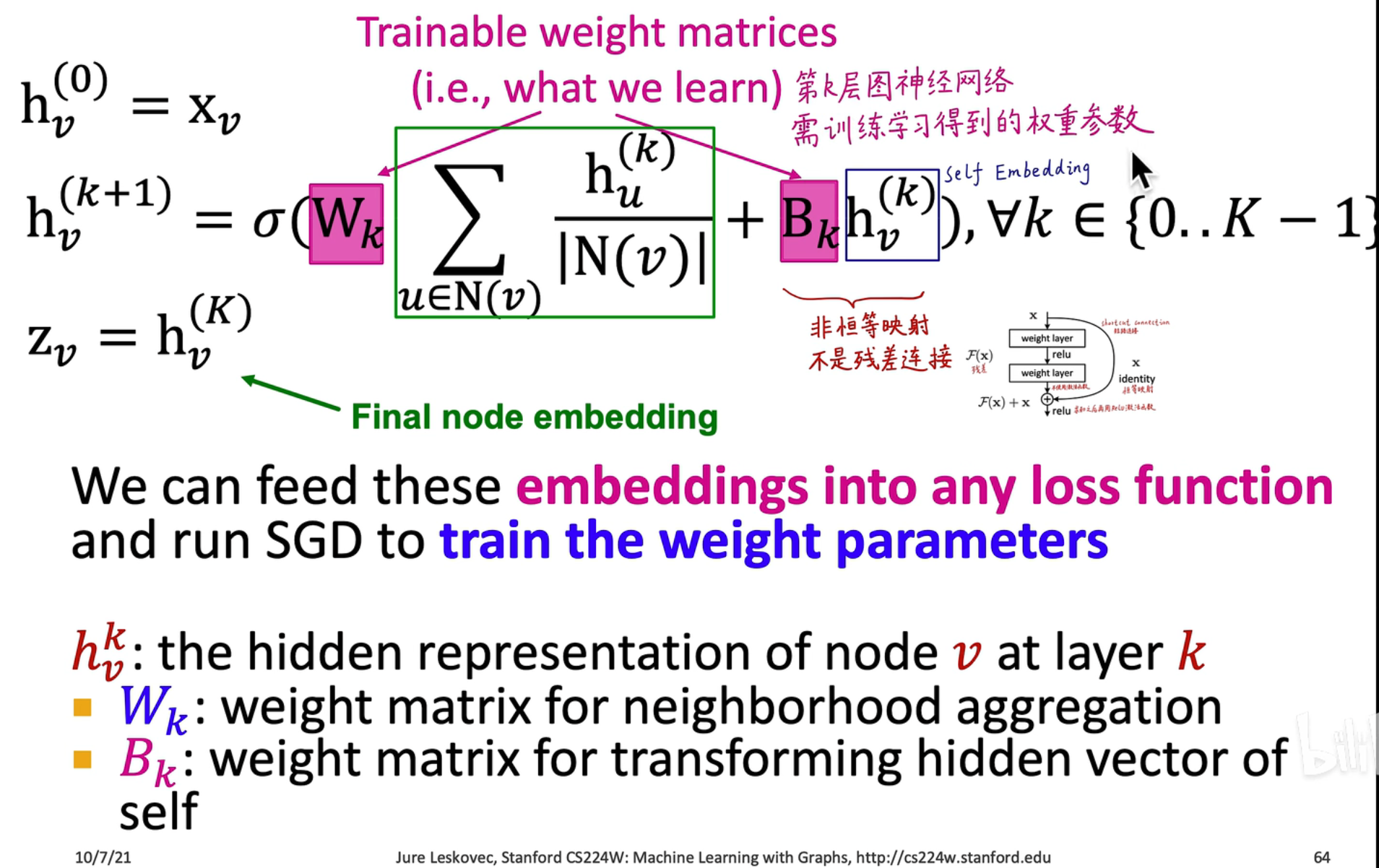
再进一步,可以将自身的嵌入和其它特征的嵌入分开表示,使用 学习其它特征的嵌入,使用 学习自身的嵌入
细节讨论
训练图神经网络
 对于半监督学习和监督学习,我们只需要对有标签的节点计算损失,损失函数通常可以选择交叉熵/均方差等等…
对于无监督学习,节点无标签,可以使用 DeepWalk/Node2Vec 的思路,直接用图自身结构作为标注,即相邻的点嵌入向量尽可能接近
对于半监督学习和监督学习,我们只需要对有标签的节点计算损失,损失函数通常可以选择交叉熵/均方差等等…
对于无监督学习,节点无标签,可以使用 DeepWalk/Node2Vec 的思路,直接用图自身结构作为标注,即相邻的点嵌入向量尽可能接近
-
有监督学习的一个例子
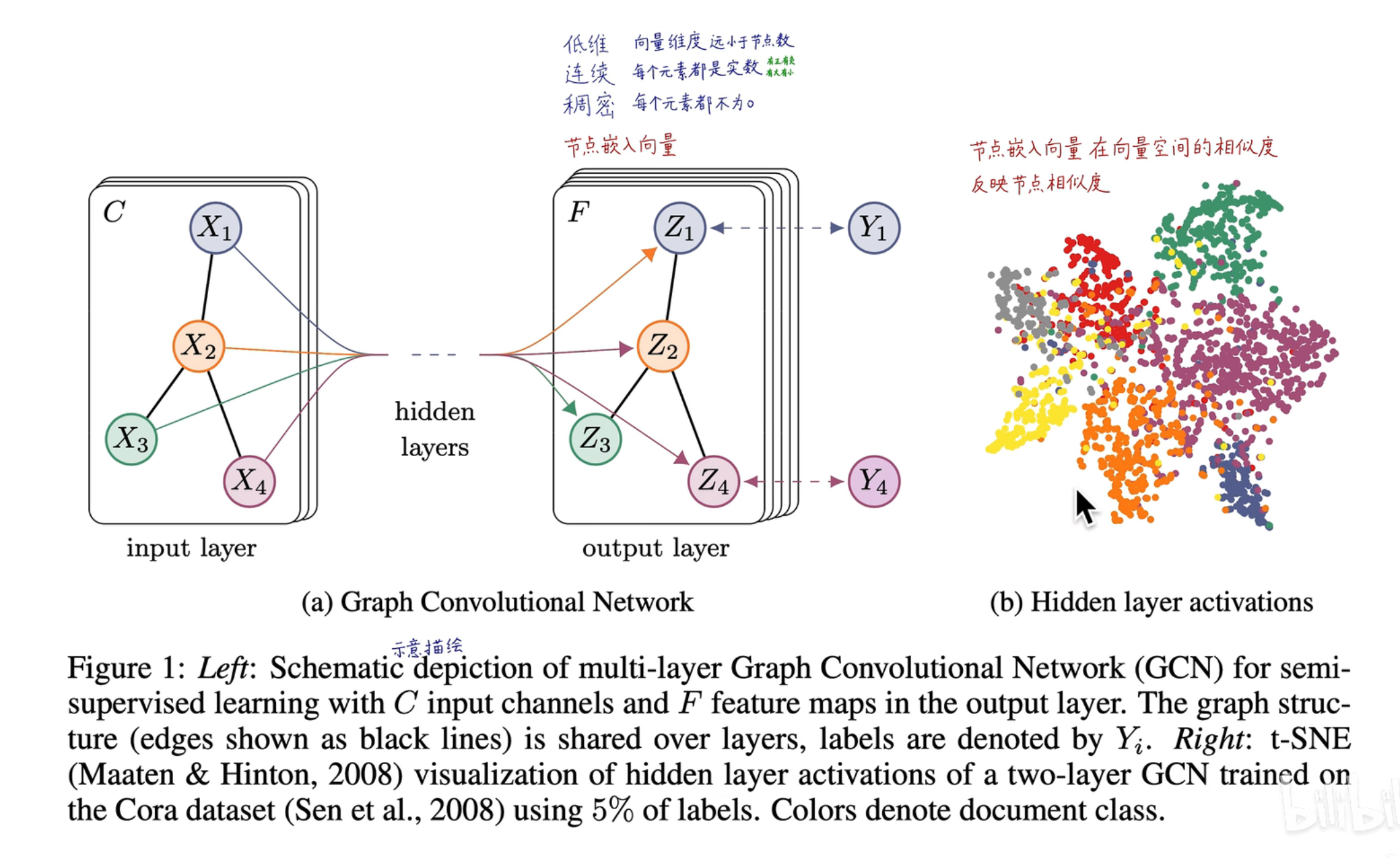
Note
图神经网络相当于一个编码器,将输入的数据在 d 维线性可分,之后加上一个线性分类头就可以进行在 d 维上进行分类了
-
无监督学习的例子

similarity = \cos \theta = \frac{A \cdot B}{\lvert\lvert A \rvert\rvert\cdot \lvert\lvert B \rvert\rvert},余弦越大表明距离越近,最大为 1计算两个向量的余弦相似度(点乘),通过余弦距离反映两个向量的关系 余弦距离计算公式:
GNN vs 传统算法
 传统的图嵌入学习方法通常需要维护一个特征表,通过对表的更新,从而获取其嵌入后的特征向量,缺点在于如果节点很多,那么需要维护的数据量就很大
传统的图嵌入学习方法通常需要维护一个特征表,通过对表的更新,从而获取其嵌入后的特征向量,缺点在于如果节点很多,那么需要维护的数据量就很大
- 直推式学习:在训练的过程中就要见到所有的节点,例如上图的查表方法,所有节点的特征向量必须存放在表中
- 归纳式学习⭐:例如 GraphSAGE、GAT、GIN 等 GNN 中,可以泛化到新节点,用于预测的节点在训练时没见过
传统算法的限制
-
泛化能力差
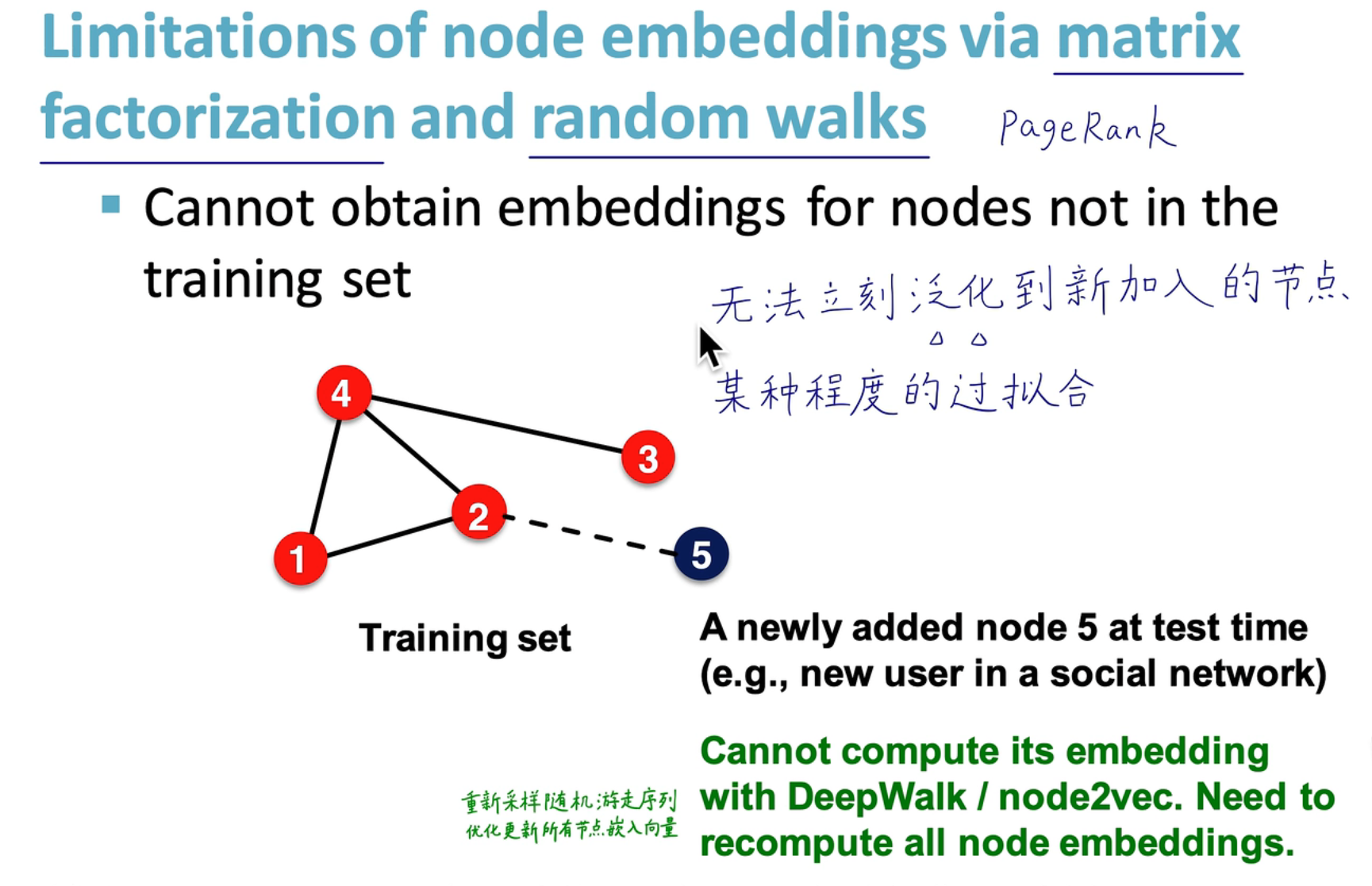 传统的算法无法对新加入的节点进行泛化,需要对整个结构重新进行一次算法迭代
传统的算法无法对新加入的节点进行泛化,需要对整个结构重新进行一次算法迭代 -
无法捕捉结构相似性
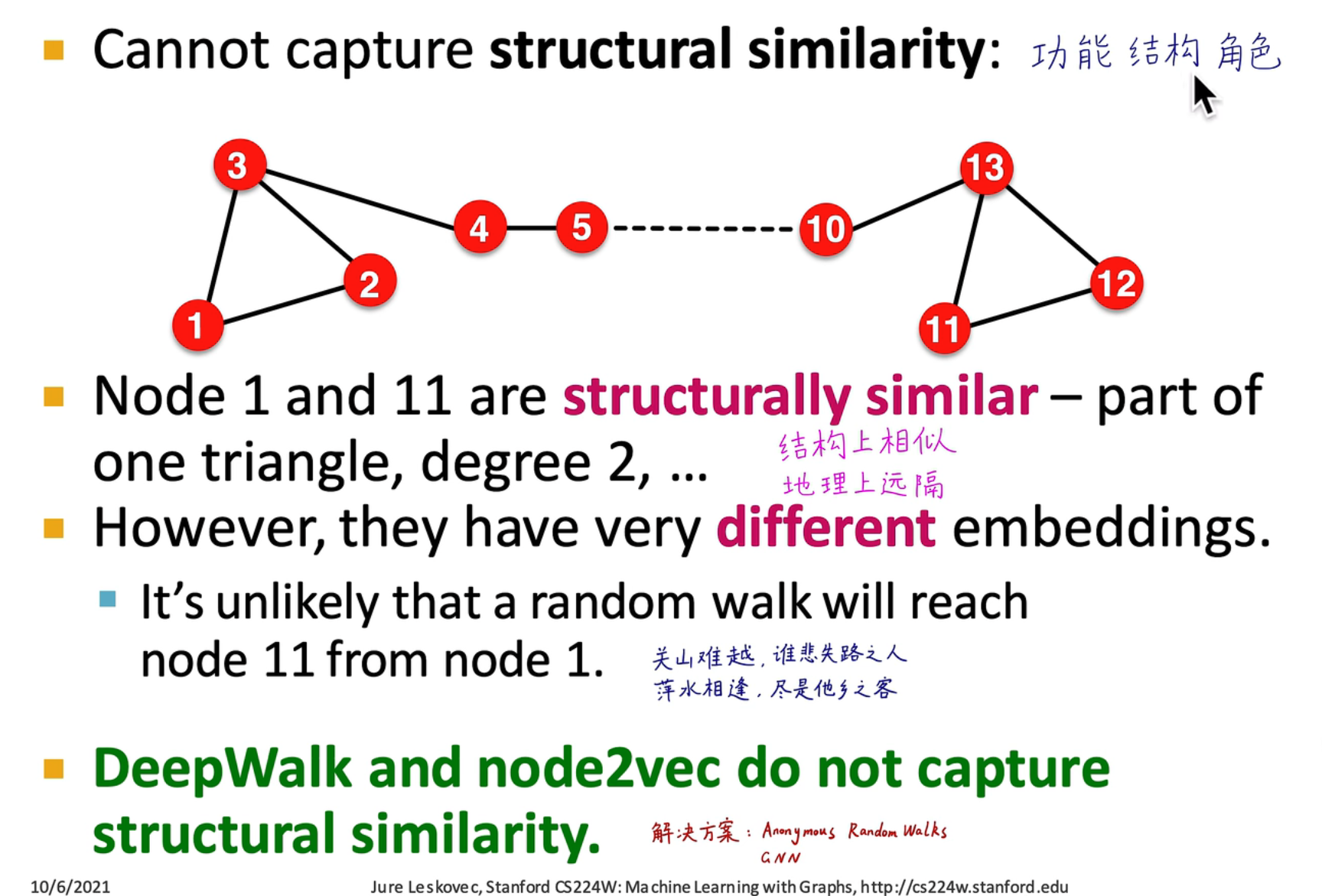 图神经网络可以捕获功能、结构、角色关系,在传统算法中,会受到最大距离限制,难以捕捉两个长距离节点之间的相关性
图神经网络可以捕获功能、结构、角色关系,在传统算法中,会受到最大距离限制,难以捕捉两个长距离节点之间的相关性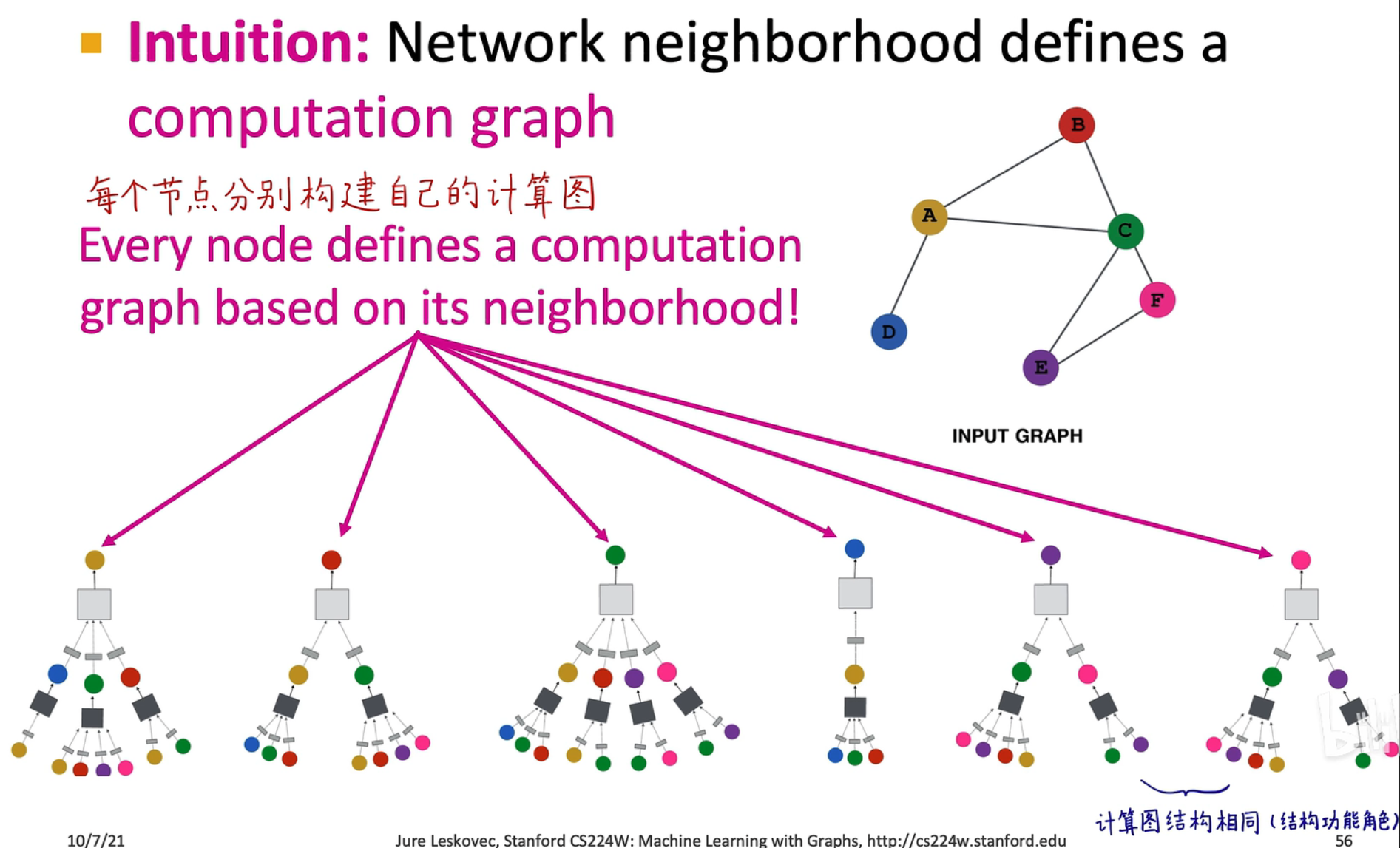 例如在上图中,紫色和粉红色节点的计算图结构相似,说明可能存在相同的结构/功能/角色,那么在计算嵌入时,它俩的嵌入特征是相似的
例如在上图中,紫色和粉红色节点的计算图结构相似,说明可能存在相同的结构/功能/角色,那么在计算嵌入时,它俩的嵌入特征是相似的 -
不能完全利用连接和属性信息
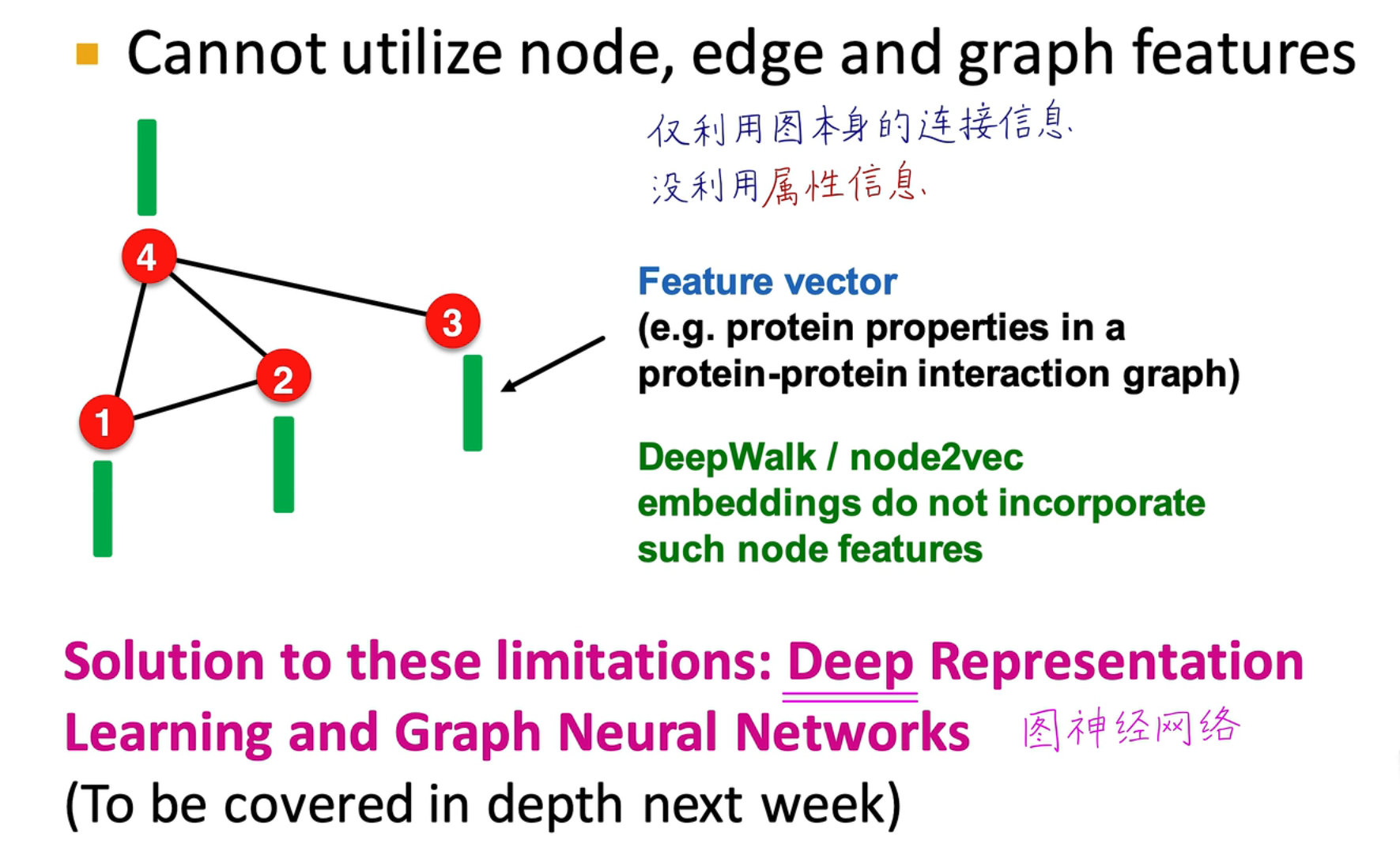 传统算法只利用了图的连接信息,没有利用属性特征
传统算法只利用了图的连接信息,没有利用属性特征
Summary

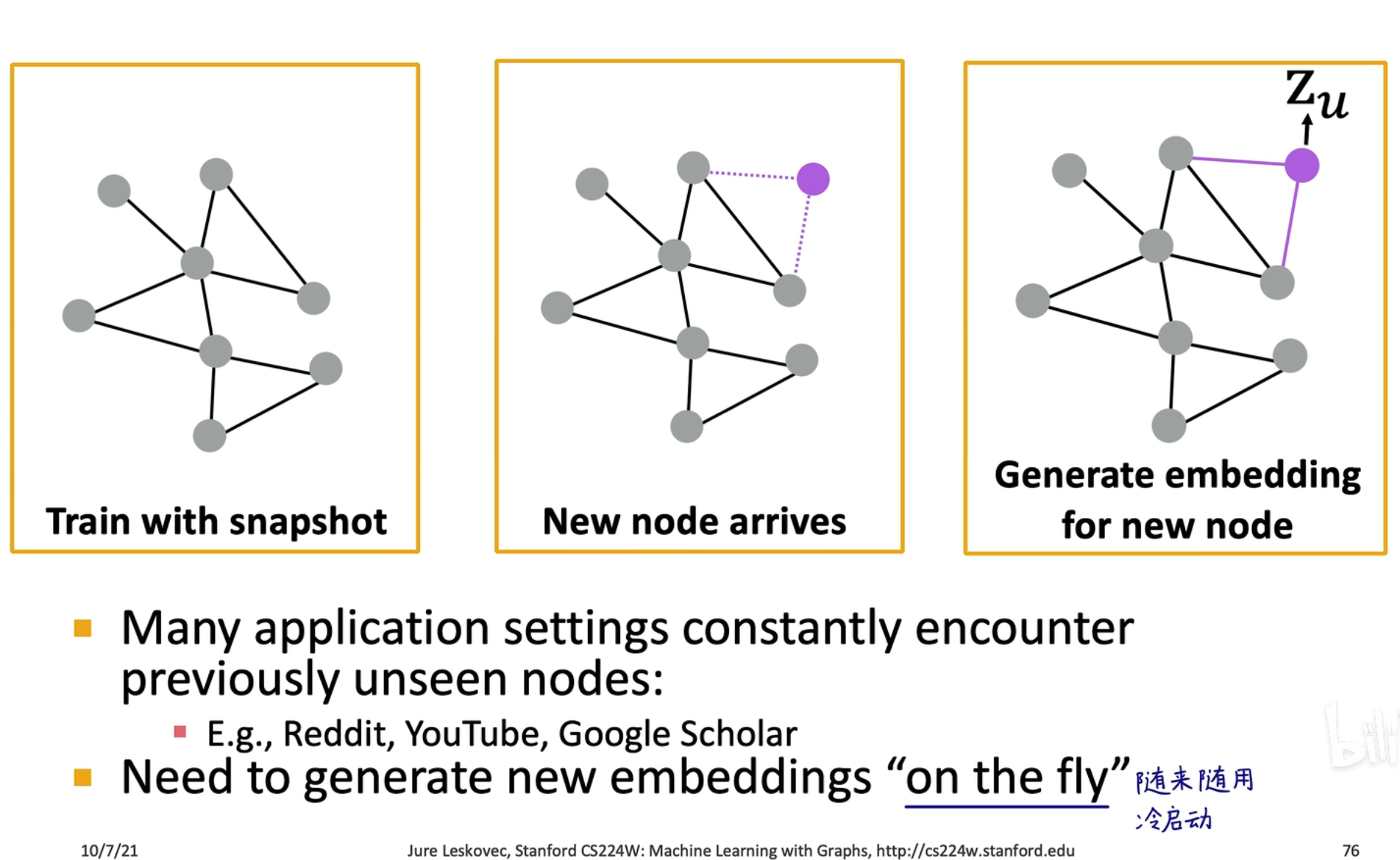 对于新的节点可以快速生成该节点的嵌入特征
对于新的节点可以快速生成该节点的嵌入特征
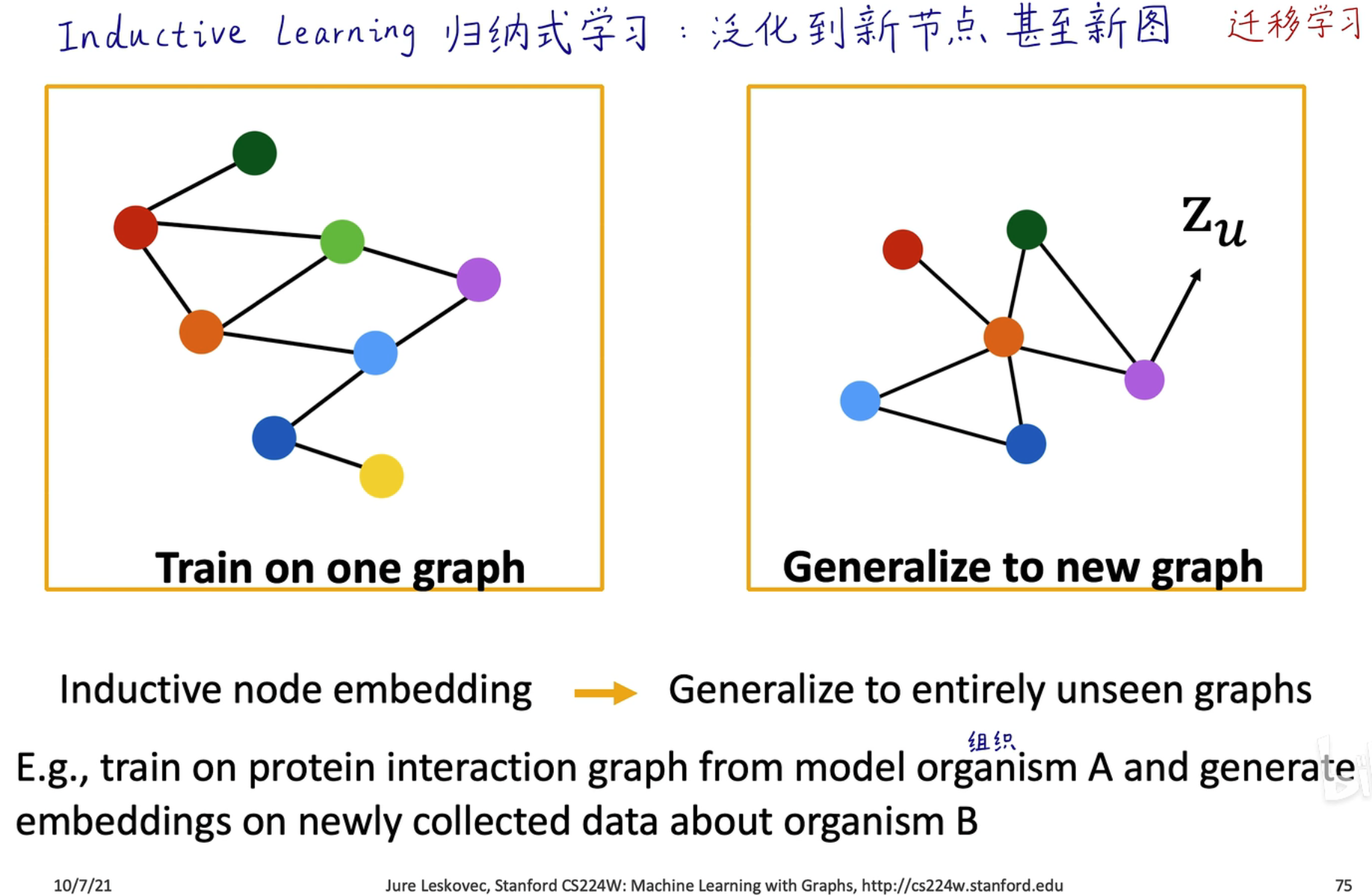 甚至可以进行迁移学习
甚至可以进行迁移学习
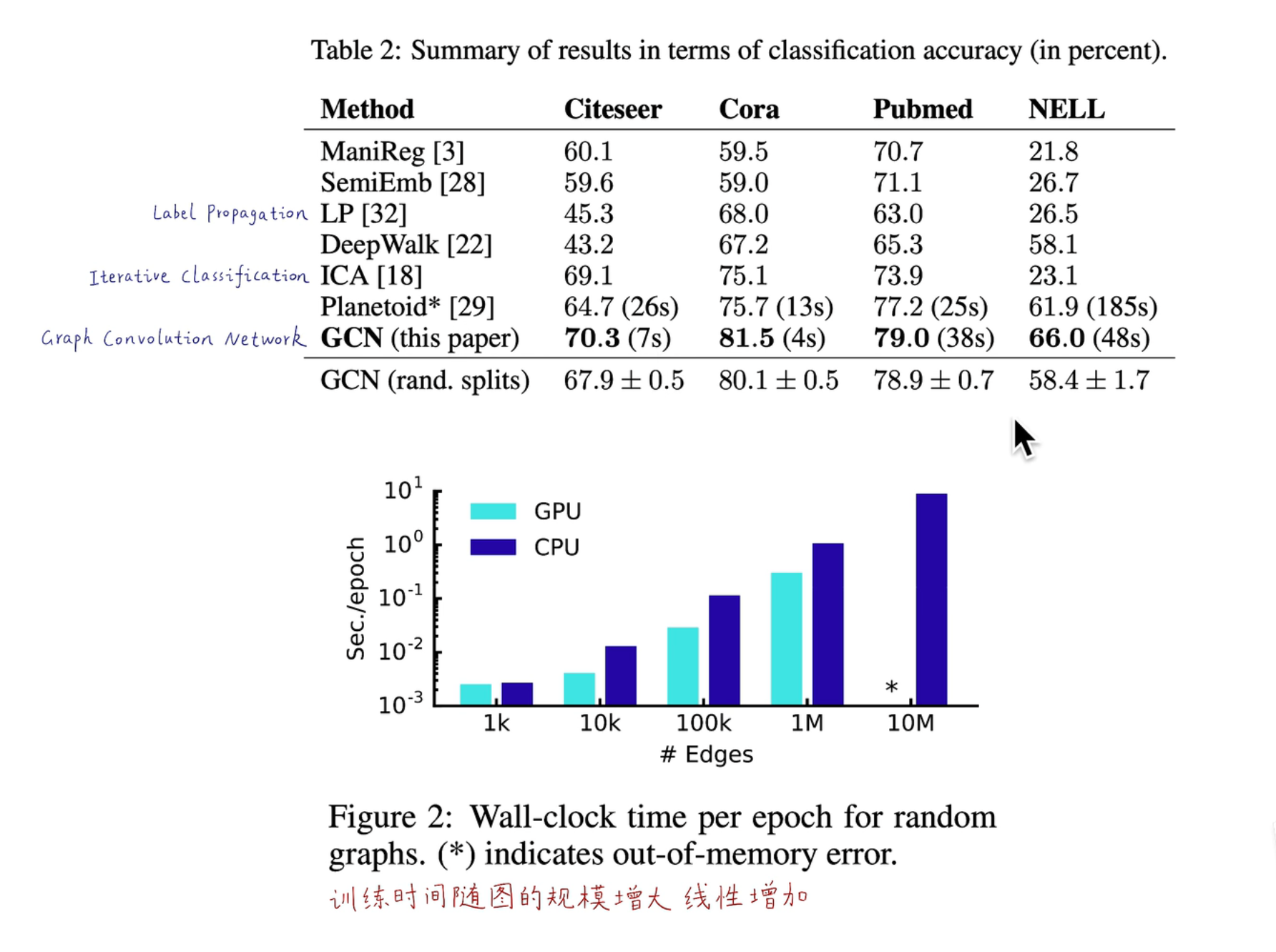 一张表可以看出 GCN 的方法要远优于传统的机器学习算法,同时算法时间复杂度是线性增加,具有很好的扩展性
一张表可以看出 GCN 的方法要远优于传统的机器学习算法,同时算法时间复杂度是线性增加,具有很好的扩展性
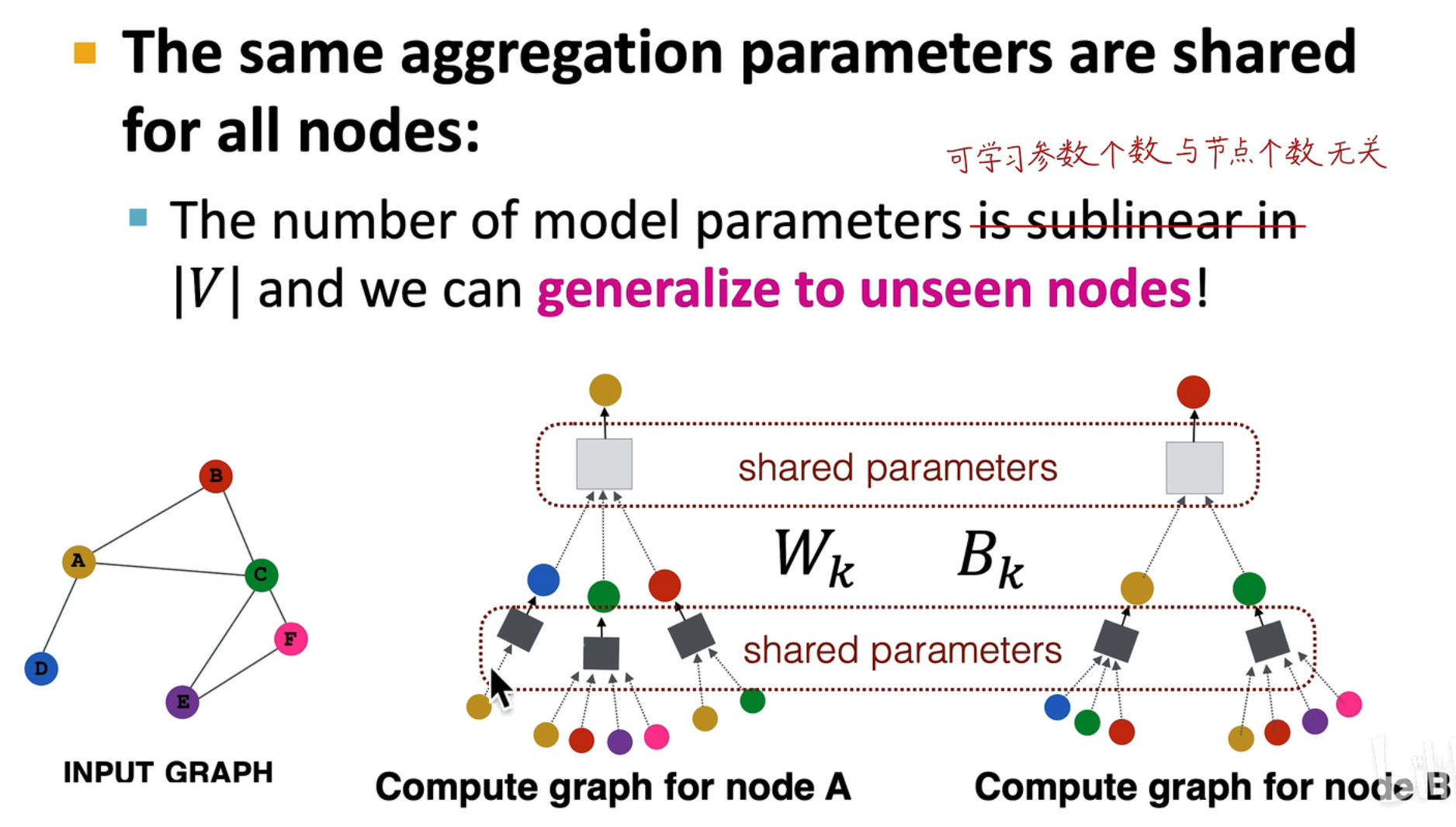 共享参数,每一层只需要训练一个网络,节点与节点之间的参数在同一层是共享的
共享参数,每一层只需要训练一个网络,节点与节点之间的参数在同一层是共享的

GNN vs CNN
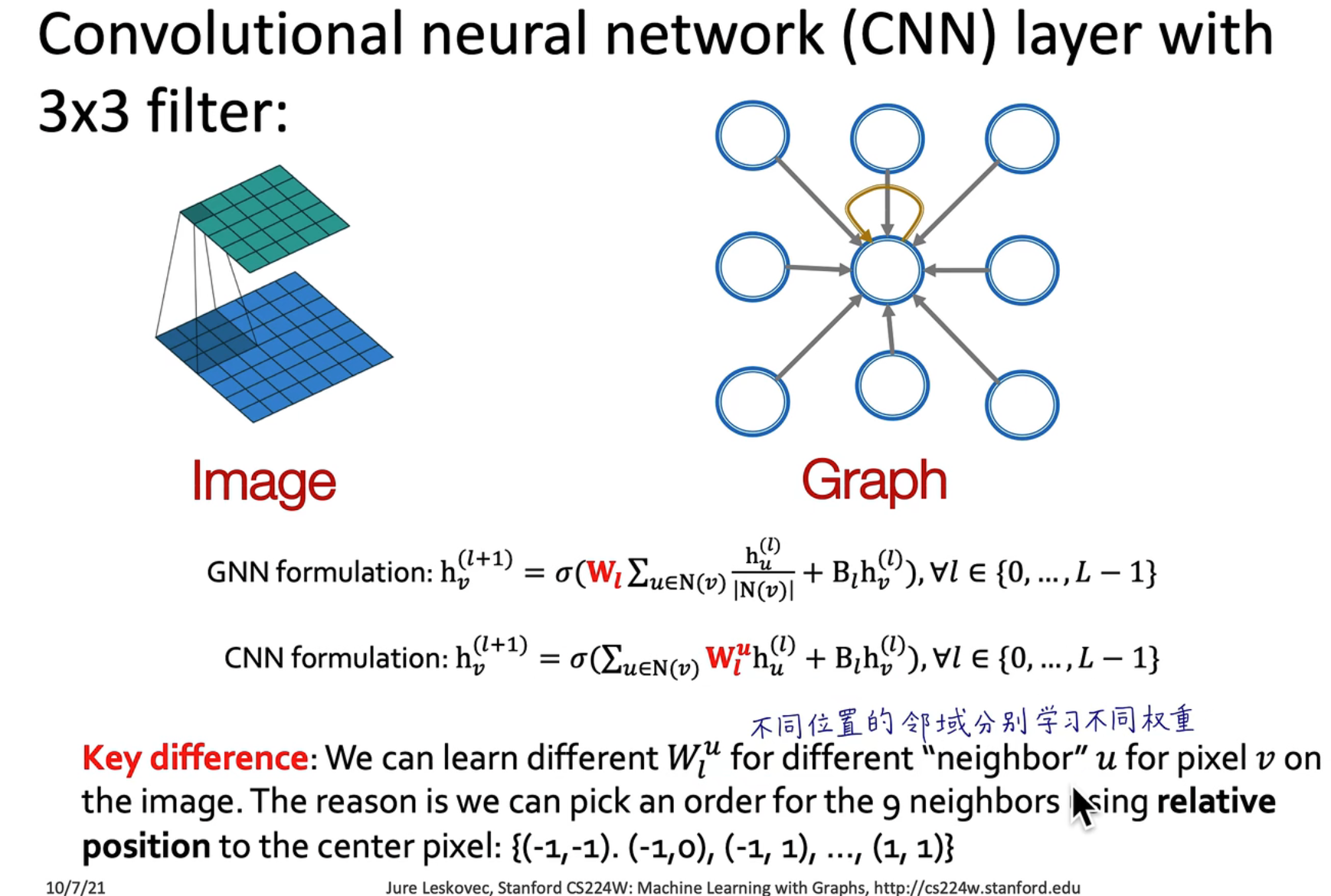
 CNN 卷积核需要学习得到,GNN 卷积核由 预定义的,和节点连接数有关
CNN 卷积核需要学习得到,GNN 卷积核由 预定义的,和节点连接数有关
 CNN 不是置换不变性的,如果像素打乱,权重没有跟着打乱,是会影响输出的;但是对于 GNN 来说,这几个都是邻域,使用共享的参数,不会对结果产生影响
CNN 不是置换不变性的,如果像素打乱,权重没有跟着打乱,是会影响输出的;但是对于 GNN 来说,这几个都是邻域,使用共享的参数,不会对结果产生影响
GNN vs Transformer
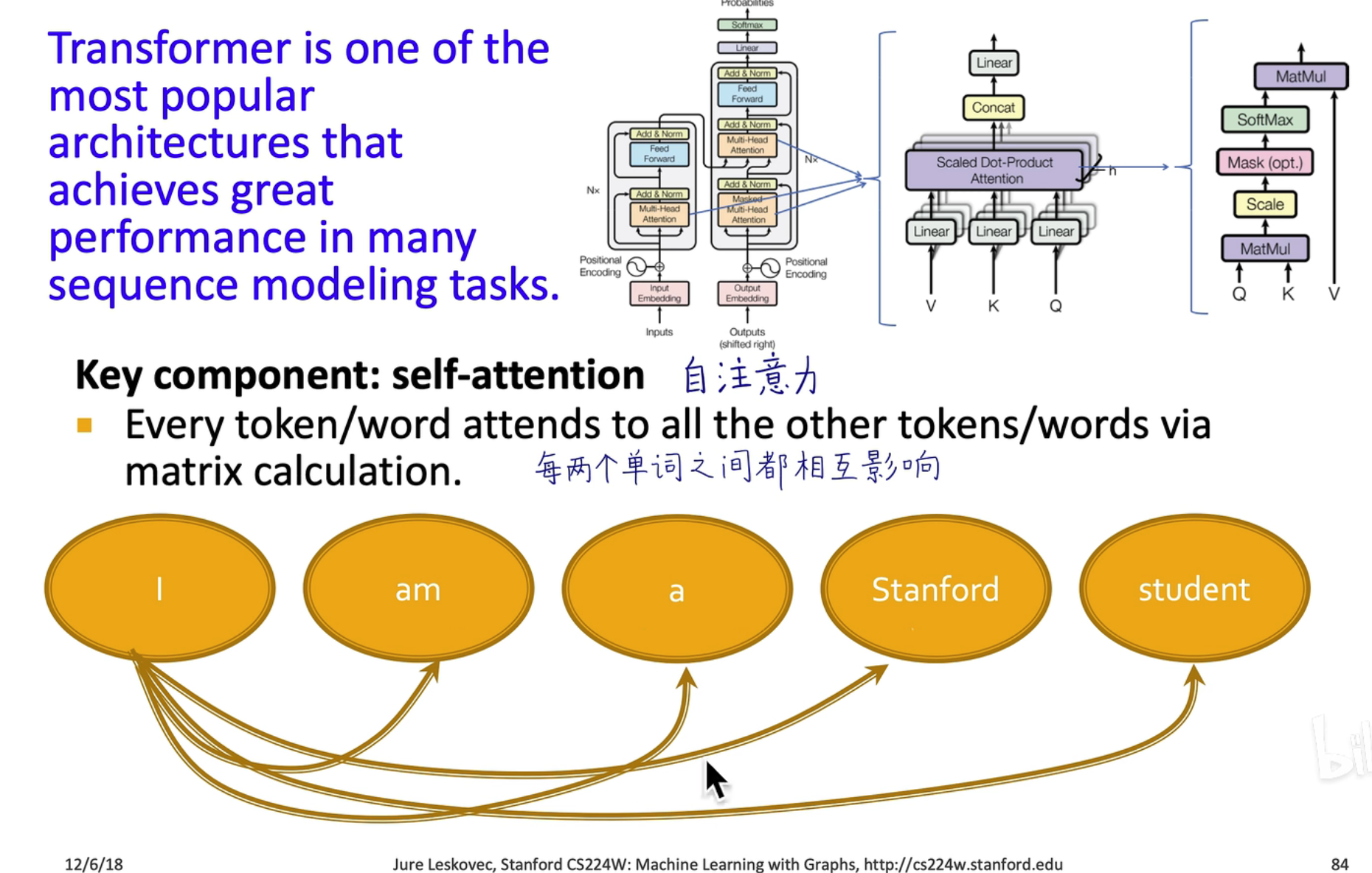
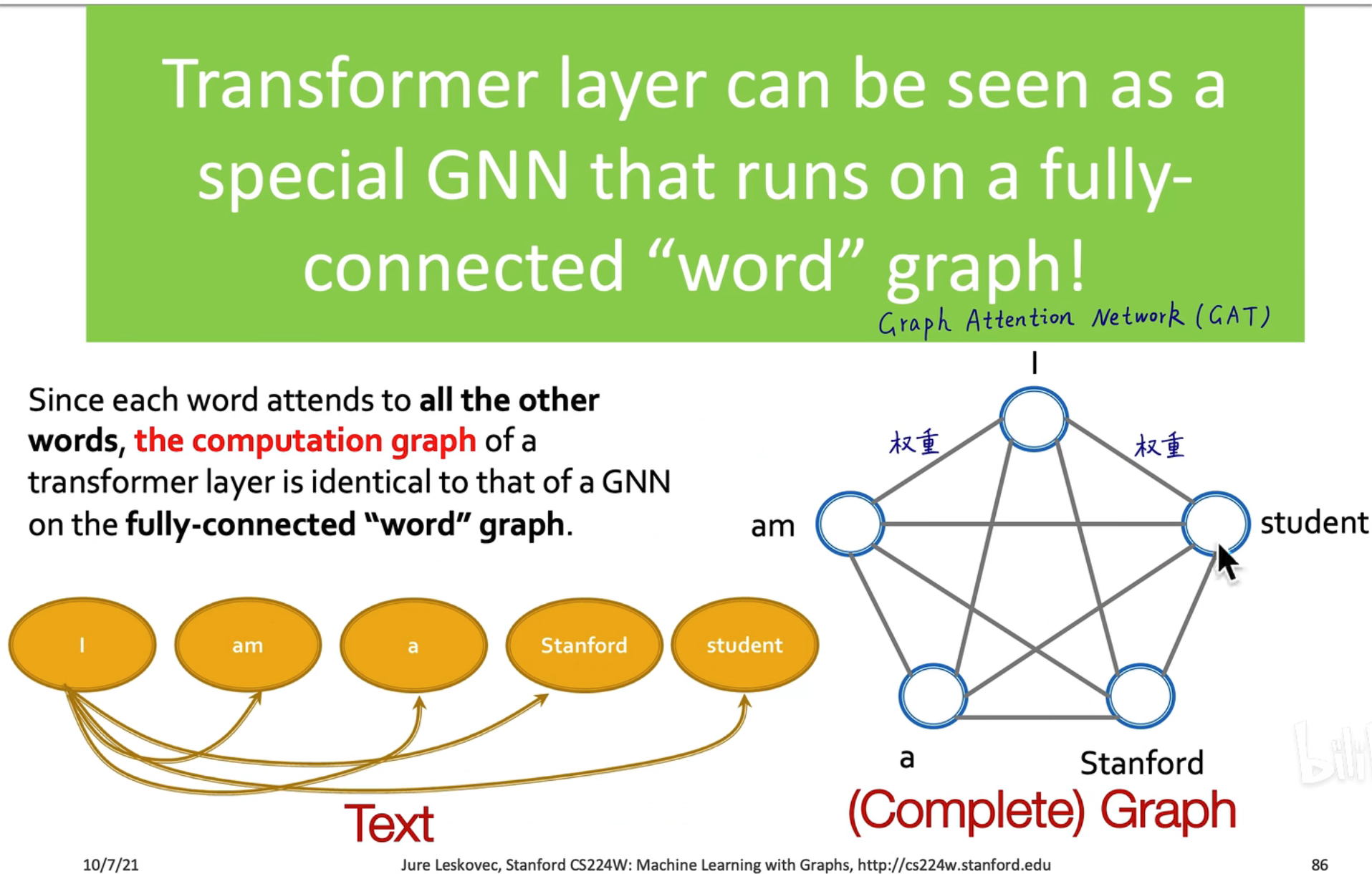 Transformer 可以看作一个全连接的 GNN,在 GNN 中也有利用注意力机制的网络,叫 GAT,在 GCN 中,是由 Normalized Adjacency Matrix 预定义的
Transformer 可以看作一个全连接的 GNN,在 GNN 中也有利用注意力机制的网络,叫 GAT,在 GCN 中,是由 Normalized Adjacency Matrix 预定义的
GNN 的表达能力
神经网络表达能力
 深度学习基石,理论上,只需要一个隐藏层就可以模拟出任意一个连续函数,前提是这个隐藏层足够有效且大,并且有一个有效的非线性的激活函数
深度学习基石,理论上,只需要一个隐藏层就可以模拟出任意一个连续函数,前提是这个隐藏层足够有效且大,并且有一个有效的非线性的激活函数
GNN 的表达能力
 GNN 的表达能力就是区分图结构的能力,表达能力最强的 GNN 模型就是 GIN
GNN 的表达能力就是区分图结构的能力,表达能力最强的 GNN 模型就是 GIN
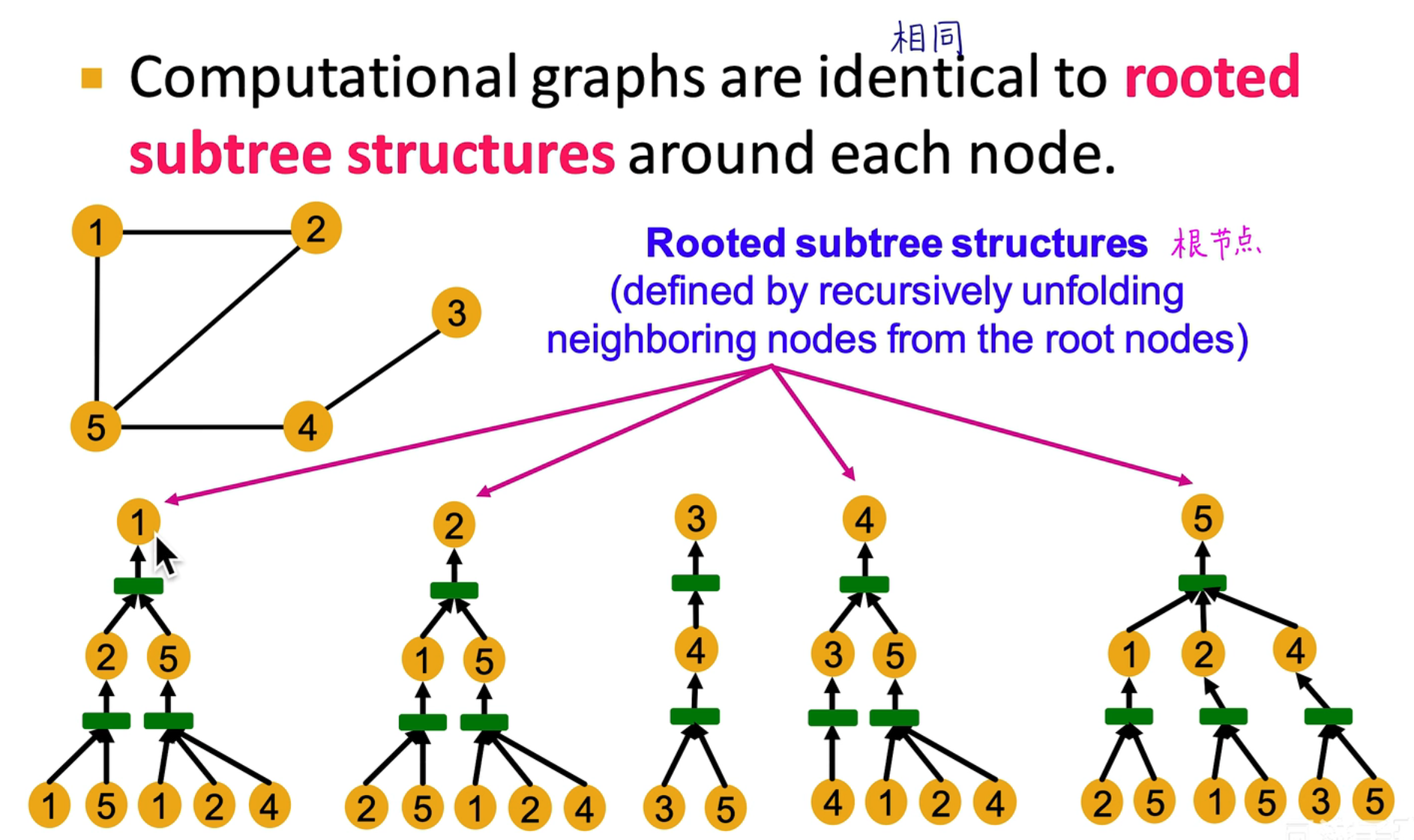 从上图可以看出,如果我们仅考虑图的结构,图节点之间的邻接信息,节点的邻居节点的邻接信息都是可以从图中获取的,通过消息传递机制都可以快速获取到,因此具有很强的表达能力
从上图可以看出,如果我们仅考虑图的结构,图节点之间的邻接信息,节点的邻居节点的邻接信息都是可以从图中获取的,通过消息传递机制都可以快速获取到,因此具有很强的表达能力
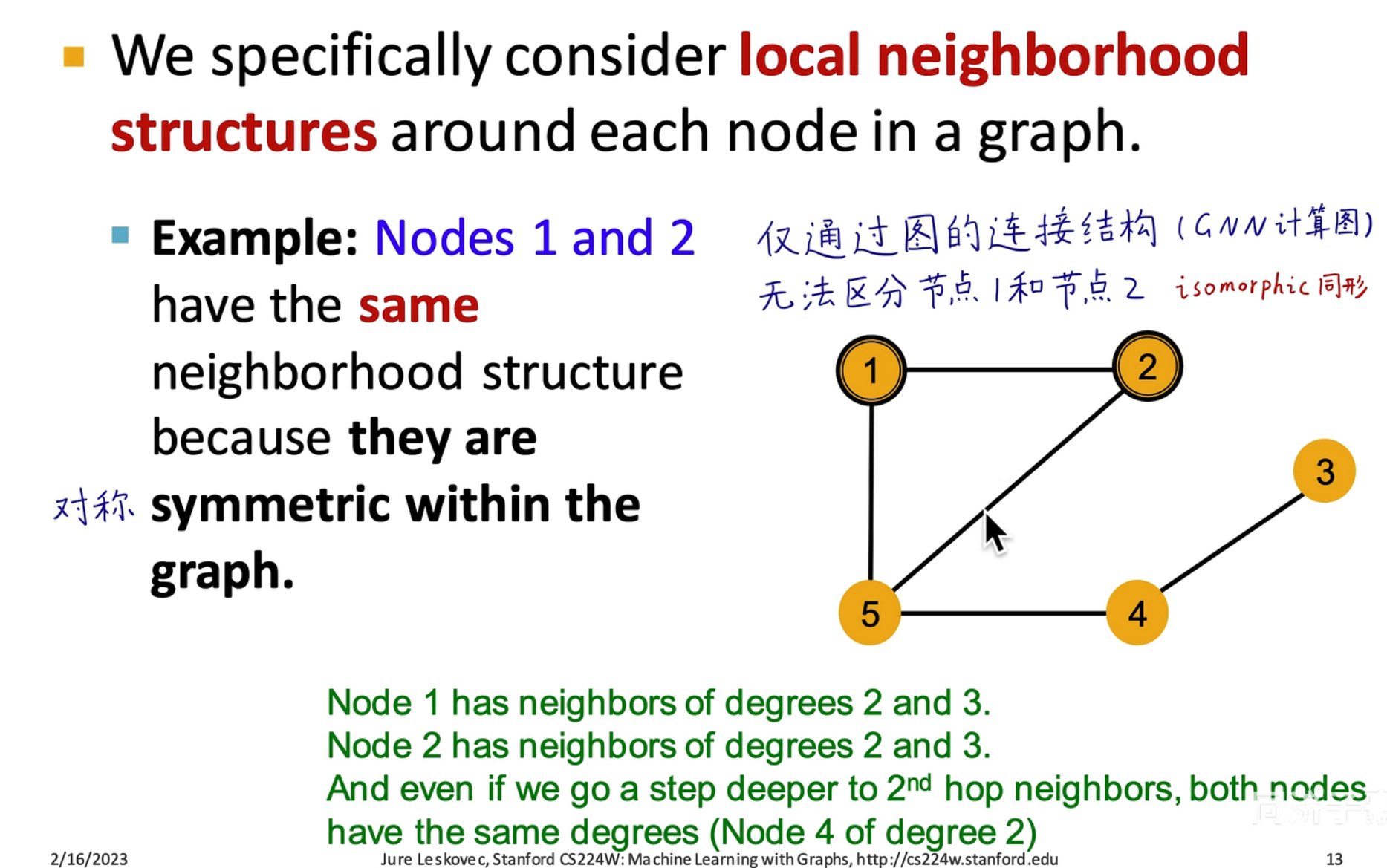 但如果是如图所示 1,2 节点是无法仅通过图的结构区分的,因为它们是同形的
但如果是如图所示 1,2 节点是无法仅通过图的结构区分的,因为它们是同形的
上面的计算图如下图所示:
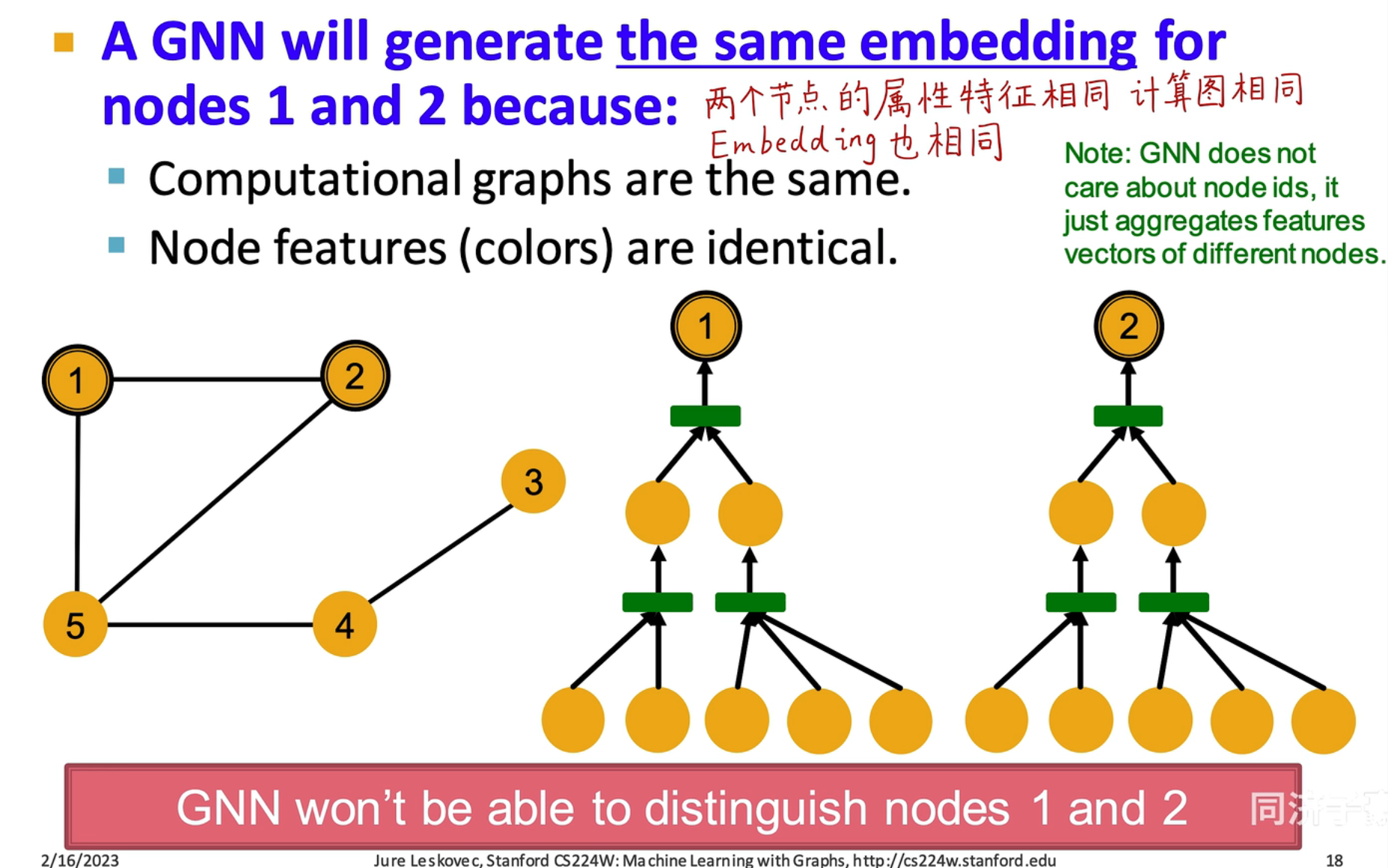 从图中可以看出,如果只考虑它们连接情况,是无法分辨出两者的不同的
从图中可以看出,如果只考虑它们连接情况,是无法分辨出两者的不同的
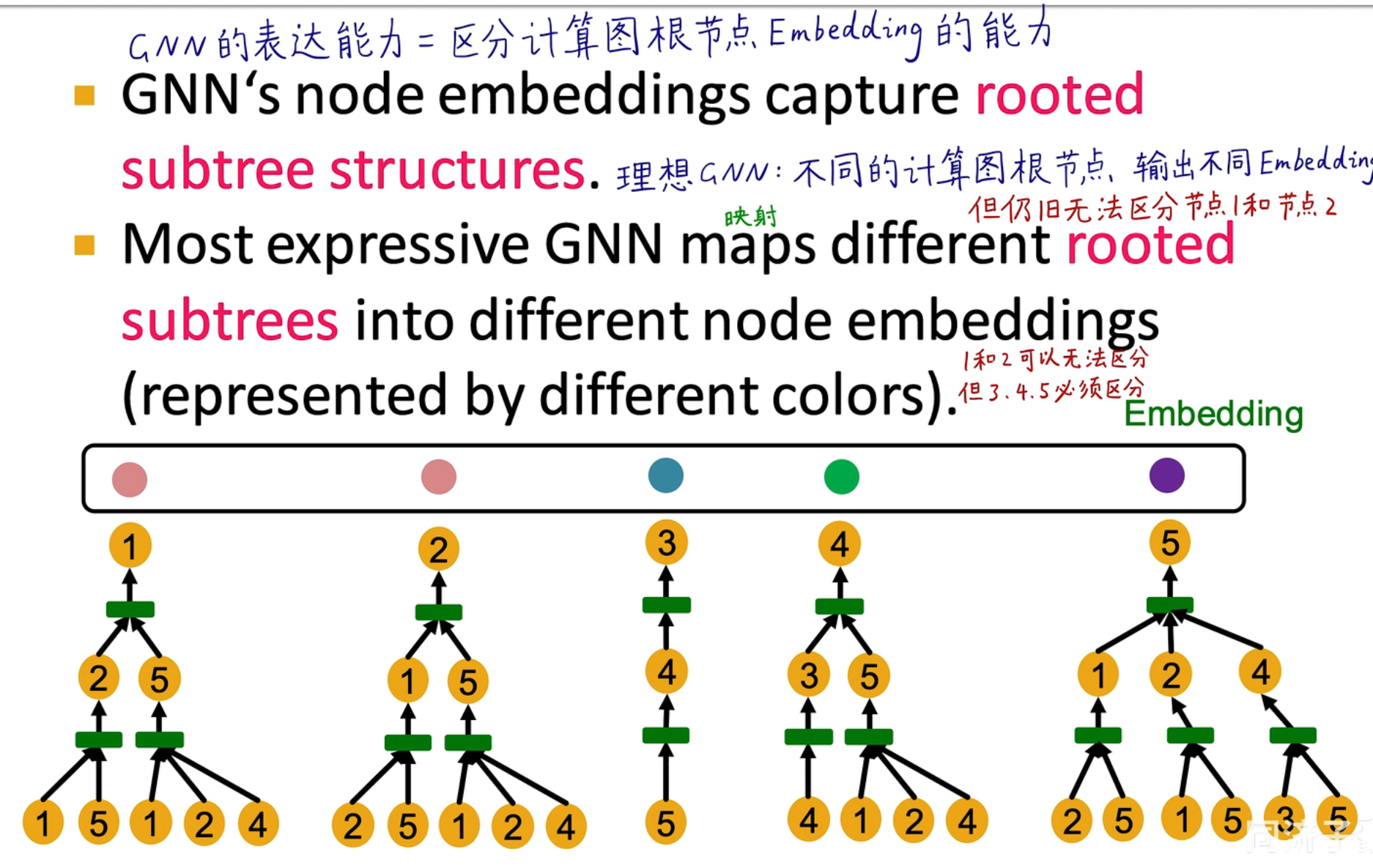 理想情况下,我们希望 3,4,5 是能够做出区分的,即计算图与 Embedding 之间是单射的!
理想情况下,我们希望 3,4,5 是能够做出区分的,即计算图与 Embedding 之间是单射的!
图神经网络表达能力对比
GCN (mean-pooling)
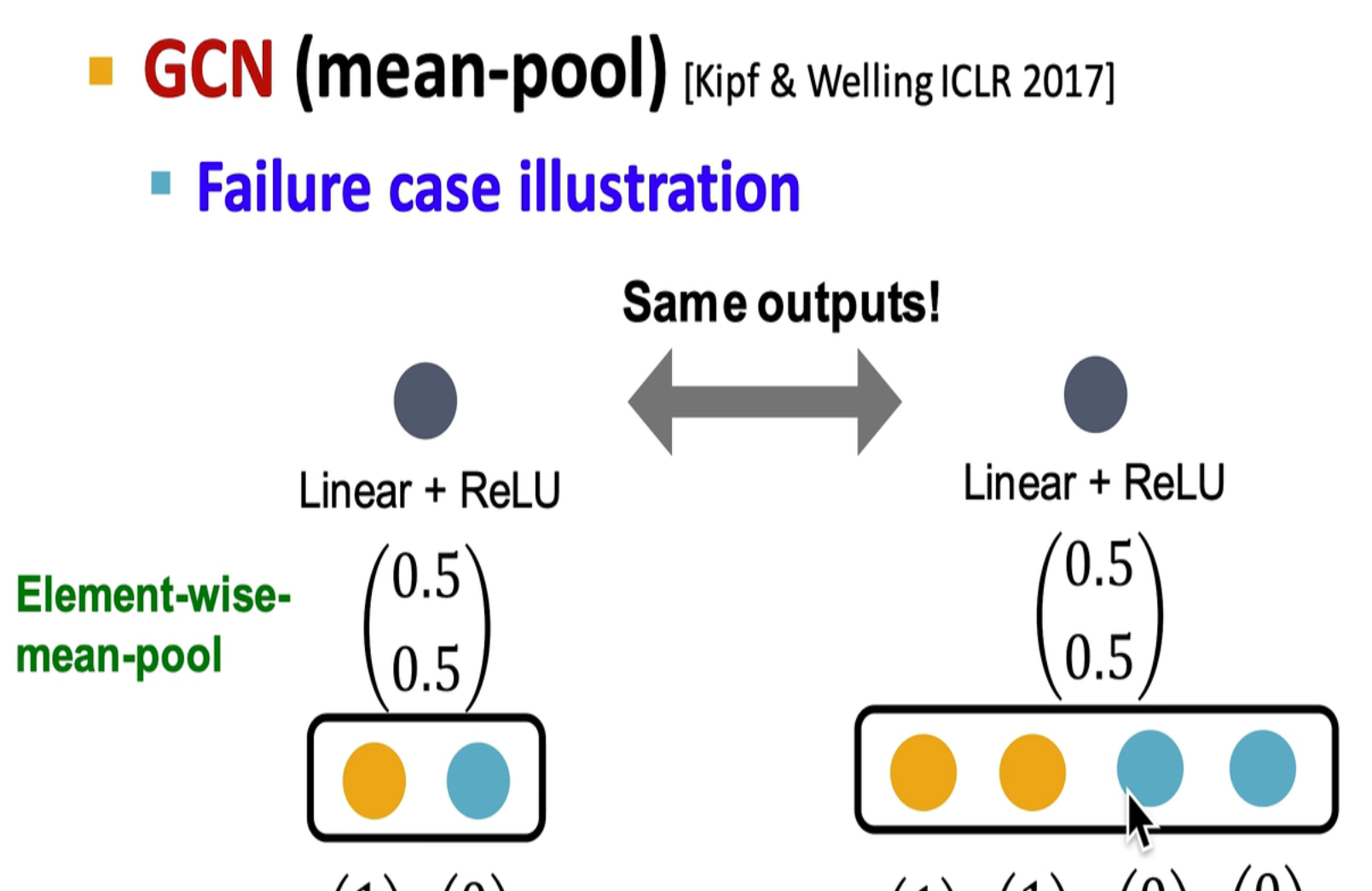
GraphSAGE(max-pooling)
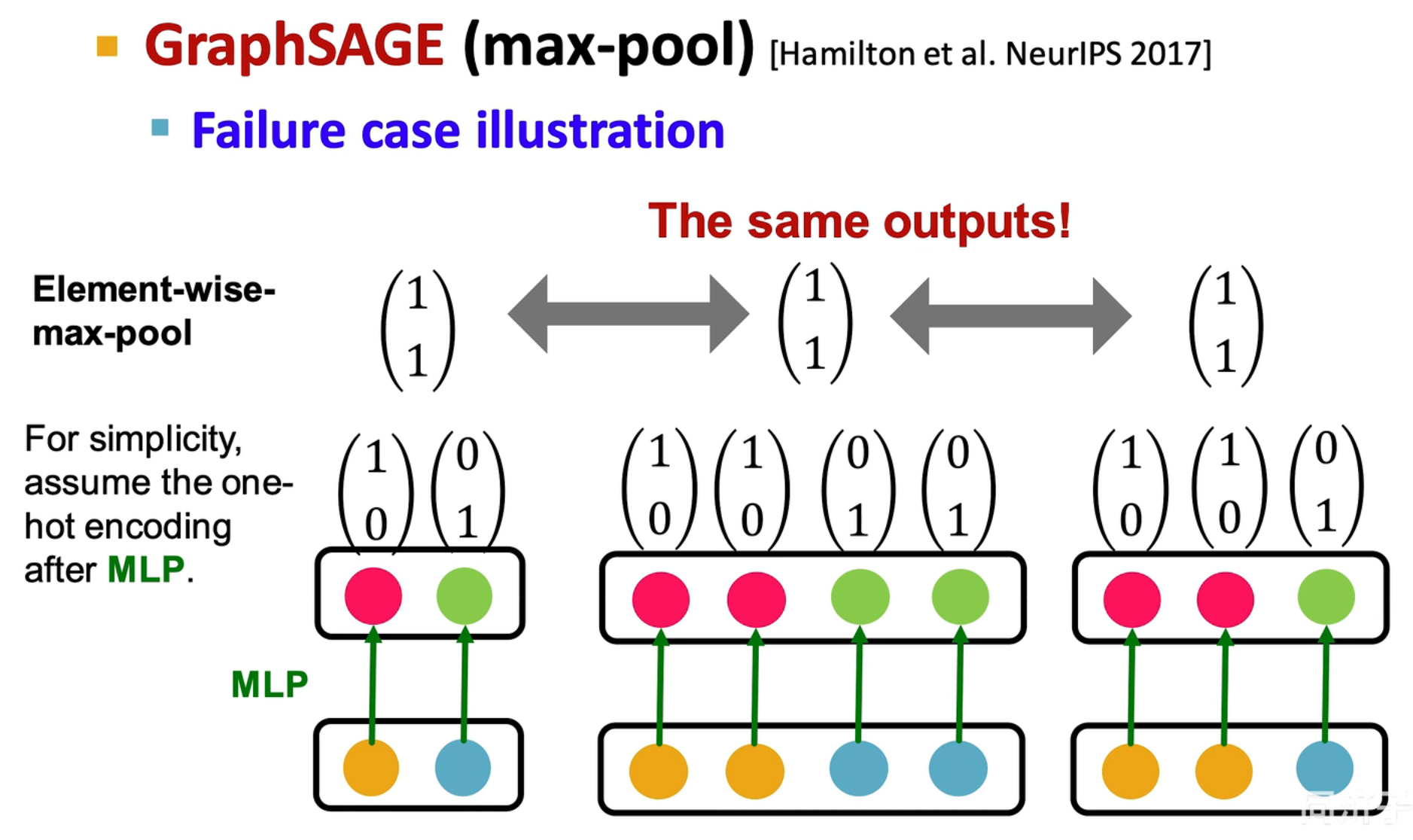
GIN
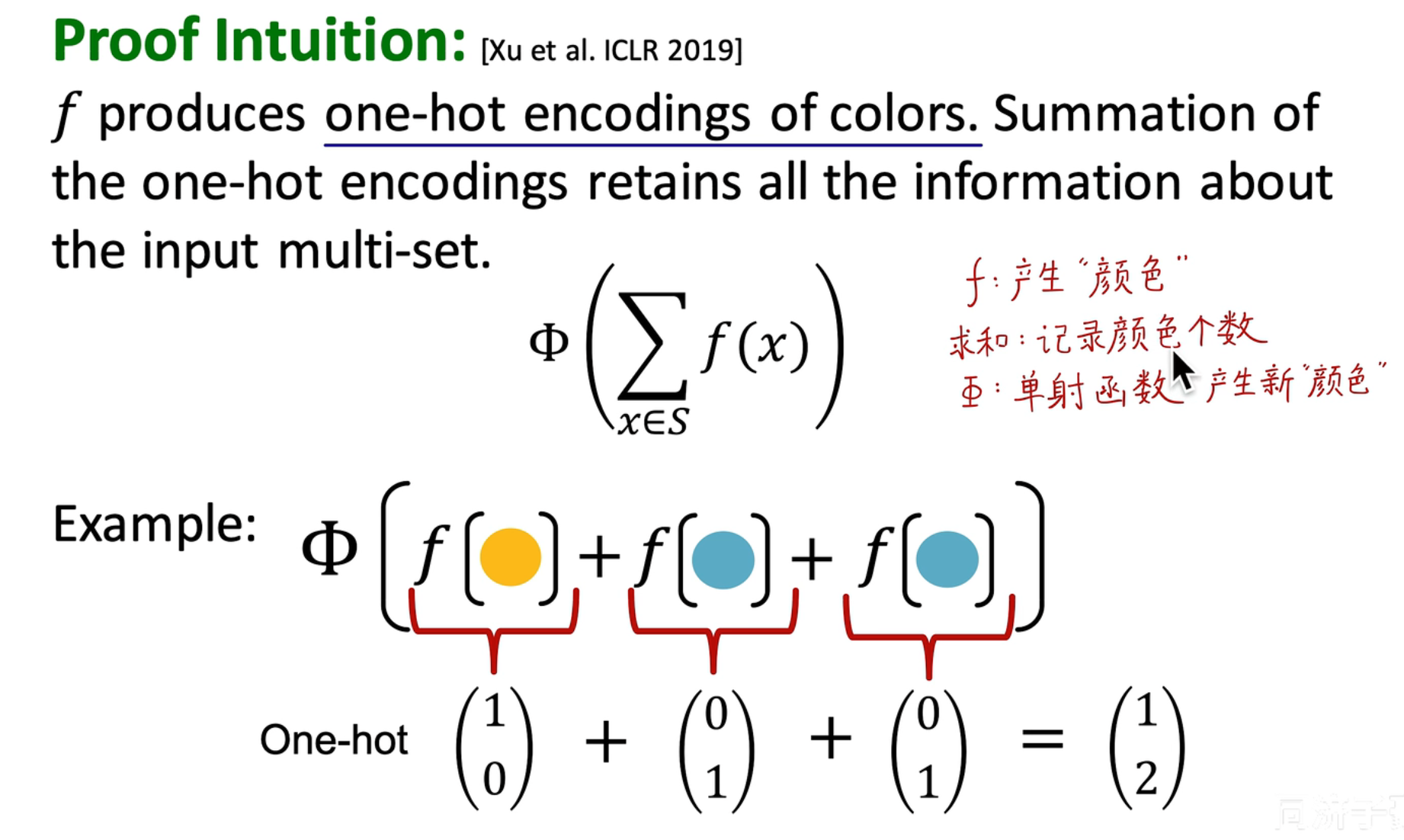
WL Kernel
step 1:通过邻居节点对节点的 embedding 进行更新
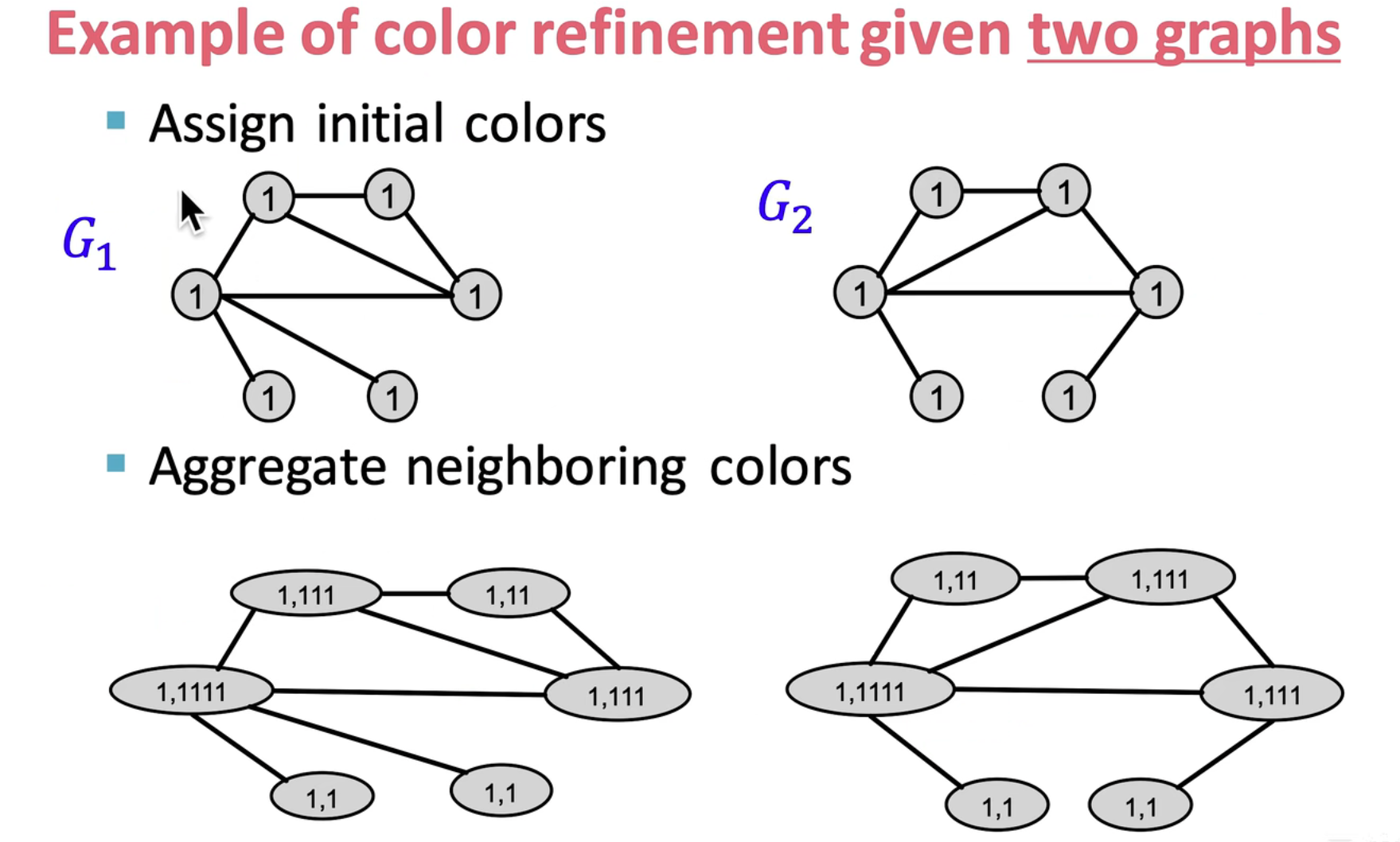 step 2:通过哈希操作对颜色进行映射,并对原来的 embedding 进行替换
step 2:通过哈希操作对颜色进行映射,并对原来的 embedding 进行替换
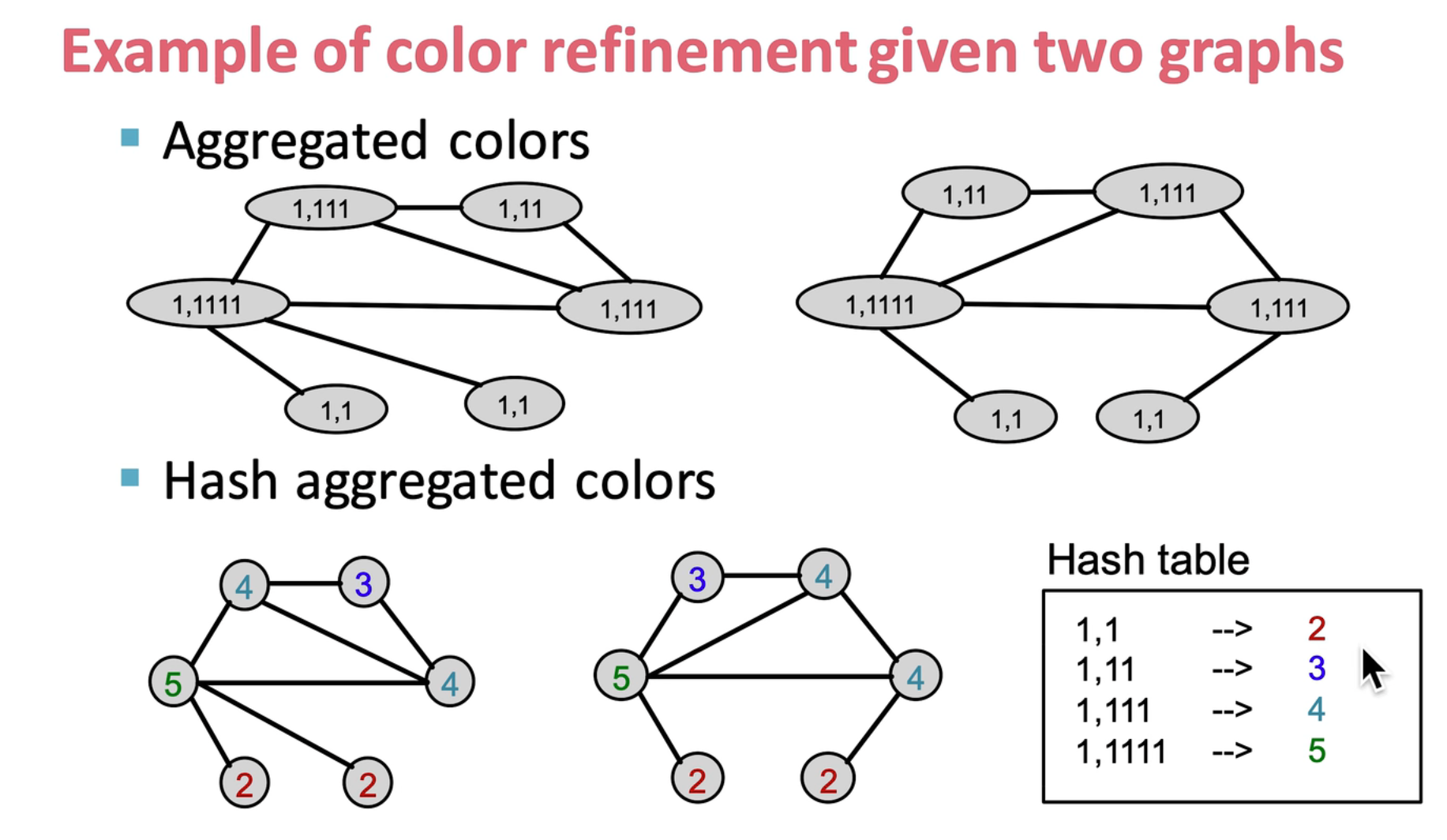 step 3:重复上面的操作,不断进行哈希操作,得到了一个最终的图 embedding
step 3:重复上面的操作,不断进行哈希操作,得到了一个最终的图 embedding
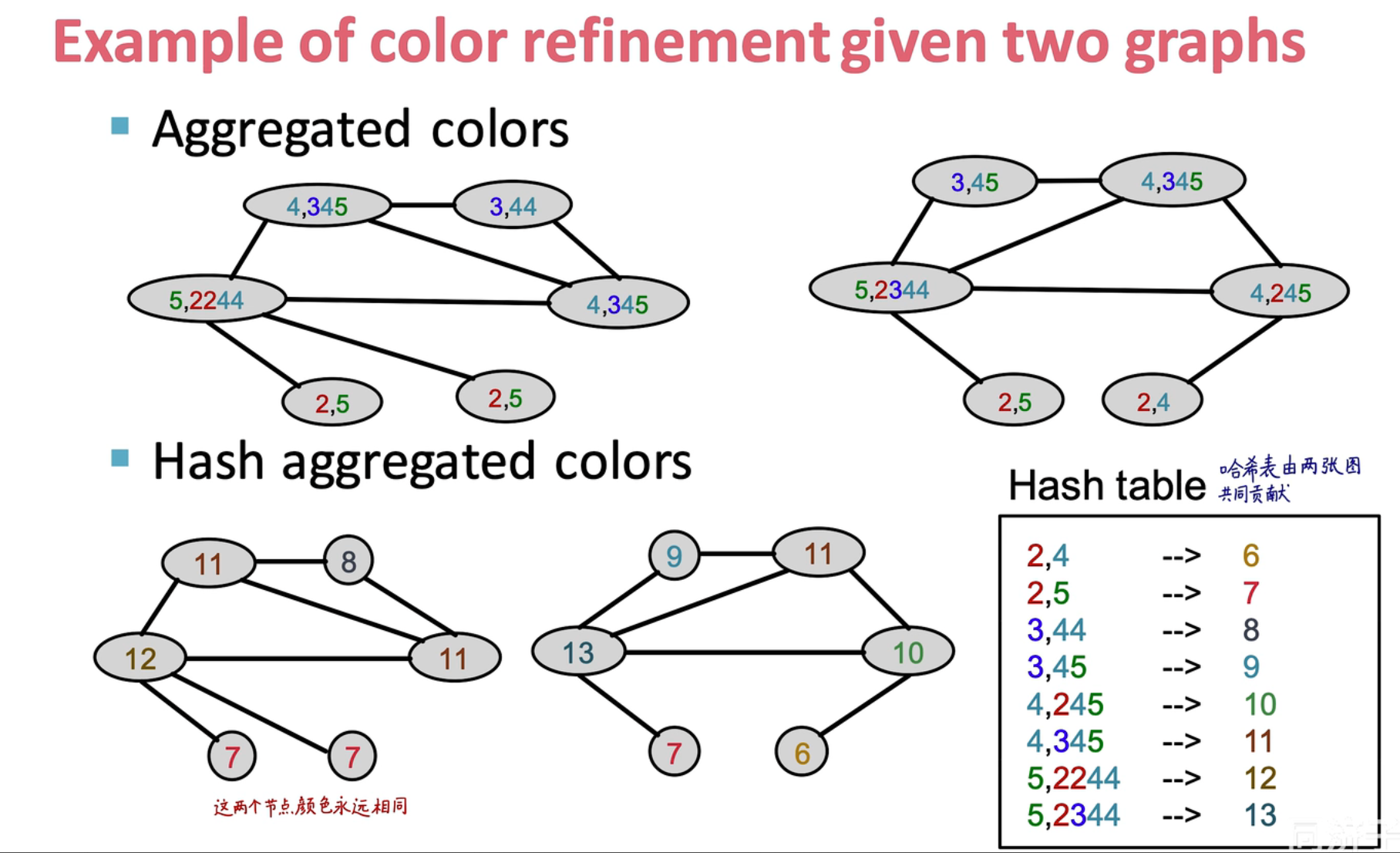 step 4:通过这些颜色 embedding 就可以对两张图的相似性进行度量
step 4:通过这些颜色 embedding 就可以对两张图的相似性进行度量
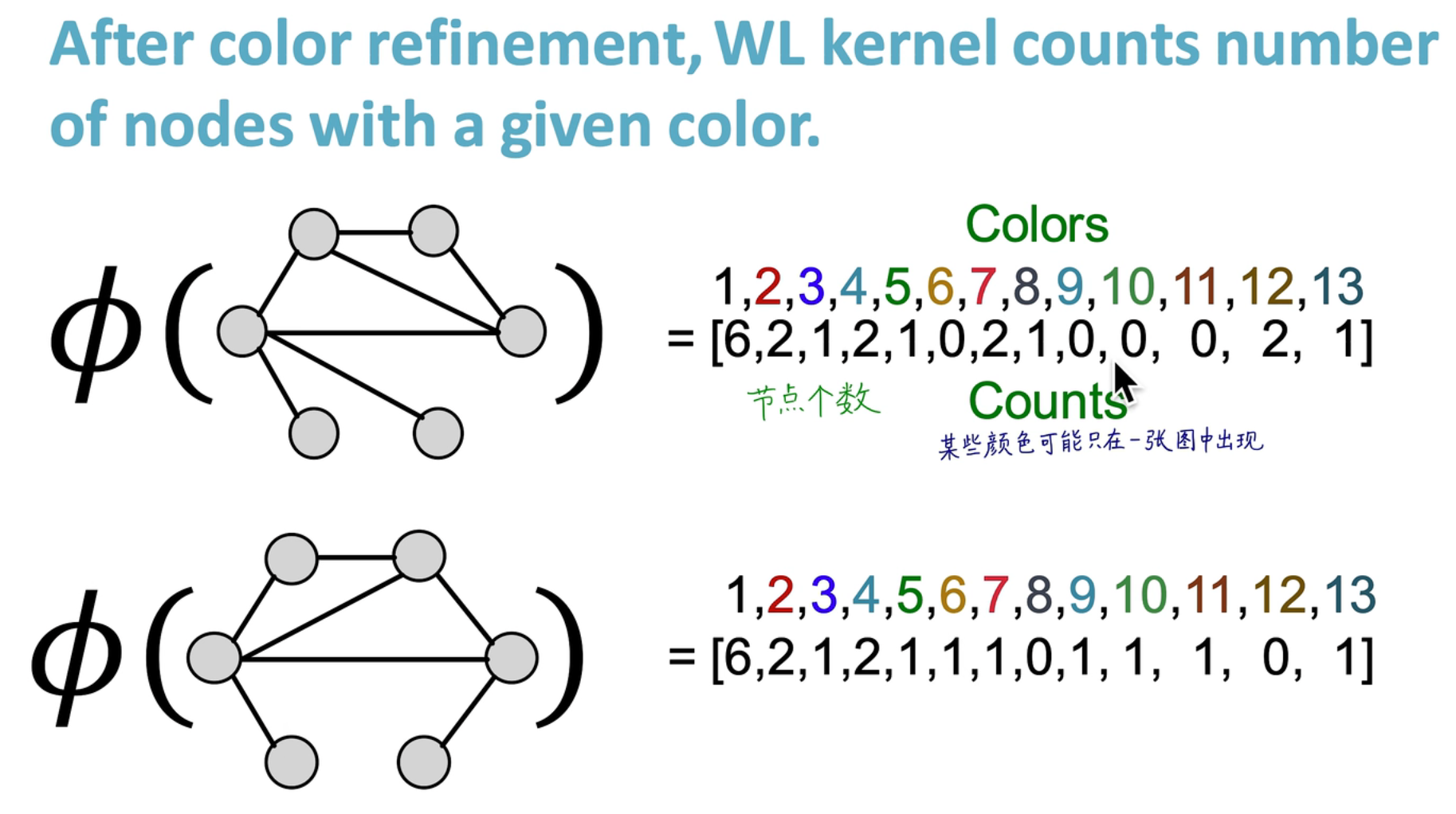
WF Kernel 和 GIN 对比

WF Kernel 是表达能力上界吗?
理论上,WF Kernel 是图结构的表达能力上界了,如果需要更强的表达能力,需要考虑添加其它信息:
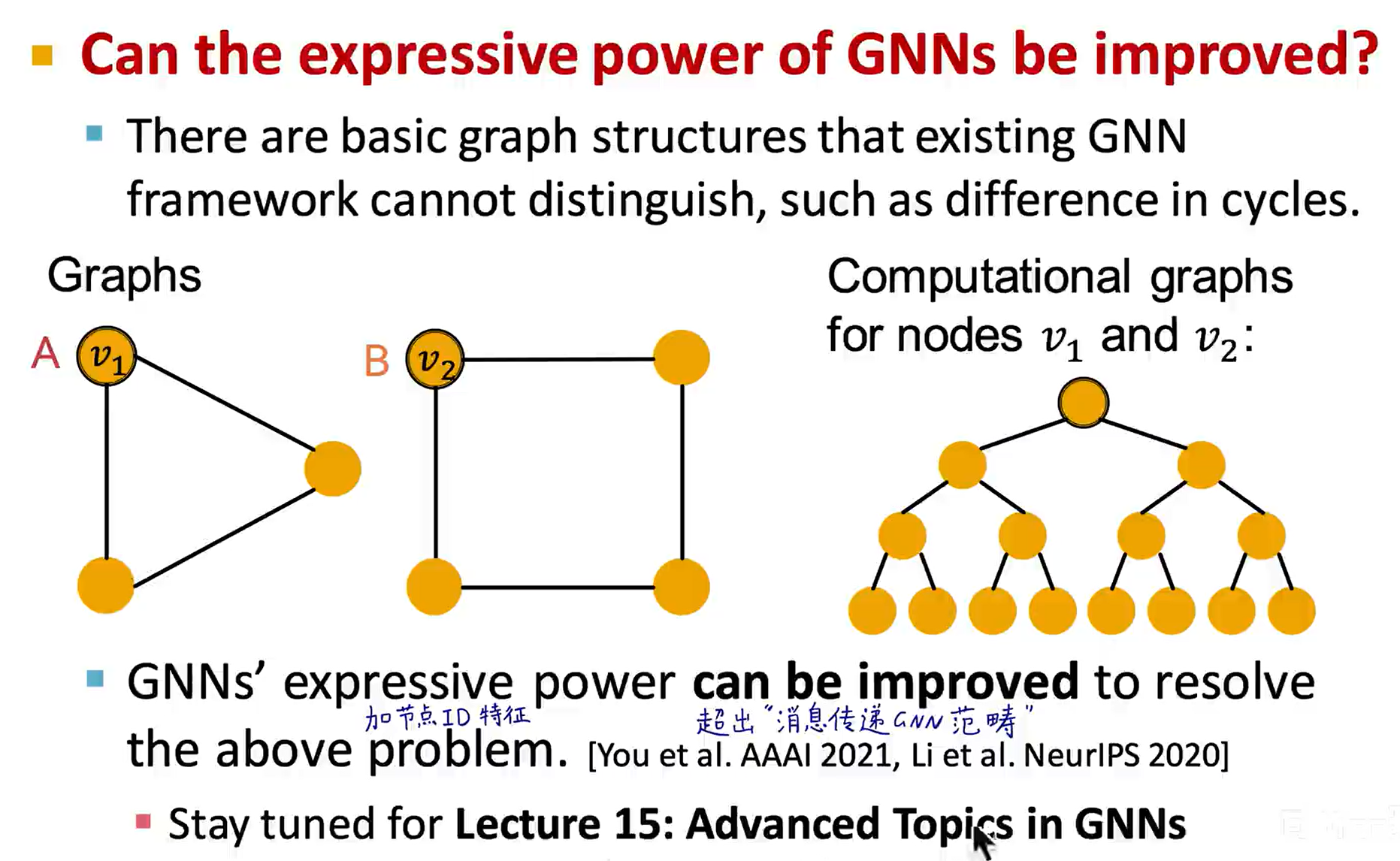
一些工程上的建议

