参考资料:
- 概率论与数理统计最后一章:置信区间与假设检验(常考题型全部团灭)_哔哩哔哩_bilibili
- 《机器学习》——周志华 P37
比较检验
有了评估方法和性能指标后,并不能直接比较相同评估方法下的性能指标大小来判断算法模型的优劣,因为在机器学习中还有如下重要因素:
- 算法希望比较泛化性能,但实验评估方法我们获得的是算法在测试集上的性能,二者的结果不一定相同
- 测试集上的性能与测试集本身关系很大,测试样例不同,测试结果可能会差距很大
- 机器学习算法本身有随机性,多次实验的结果可能都不同
☺️感谢统计学,统计假设性检验为我们提供了比较的依据。基于统计假设性检验的结果,我们可以得到结论:如果在测试集上,A 算法的表现比 B 好,则 A 的泛化性能是否在统计意义上优于 B,以及下这个结论的把握有多大
Note
注:下面的内容以错误率为性能指标,用 表示
假设检验
假设检验中的“假设”是对算法的泛化指标的某种判断/猜想,上述介绍中的因素 1 中说明测试集性能和泛化性能是可能不一致的,泛化性能是未知的,我们已知的是测试集的性能。从直观上讲,二者接近的可能性较大,相差很远的可能性很小,因此我们可以从测试集性能推测出泛化性能,并给出推测的概率分布
置信区间
首先回顾一下在考研数学一中的几个分布:
- ,标准化后:
在题目中,我们经常会遇到要求:设置信水平为 ,这里的 的含义是什么? 表示小概率事件发生的概率; 表示大概率事件发生的概率; 设置信水平为 就是将事件限制在大概率范围内
为了能够在图中很好的观察到 的置信区间,我们提出了上 分位点和下 分位点:
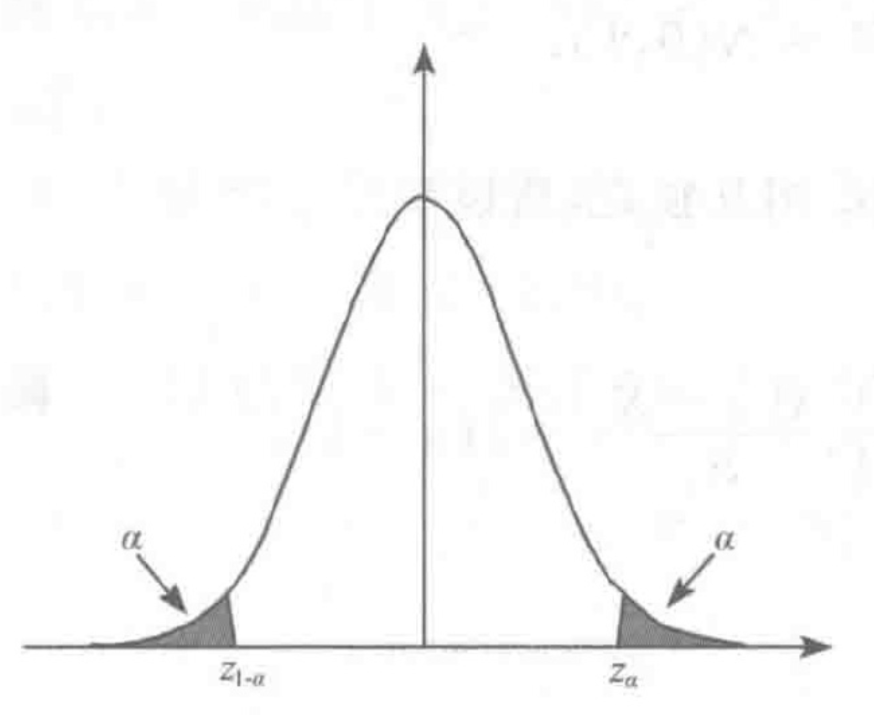 上图中展示的是 分位点, 同理,阴影部分称为拒绝域(小概率事件),剩下的部分称为置信区间
上图中展示的是 分位点, 同理,阴影部分称为拒绝域(小概率事件),剩下的部分称为置信区间
假设性检验
在假设性检验中,常见套话如下:
假设接受 ,计算 是否在大概率事件内,即拒绝域为 或 ,若落在拒绝域,则拒绝 ,反之则接受
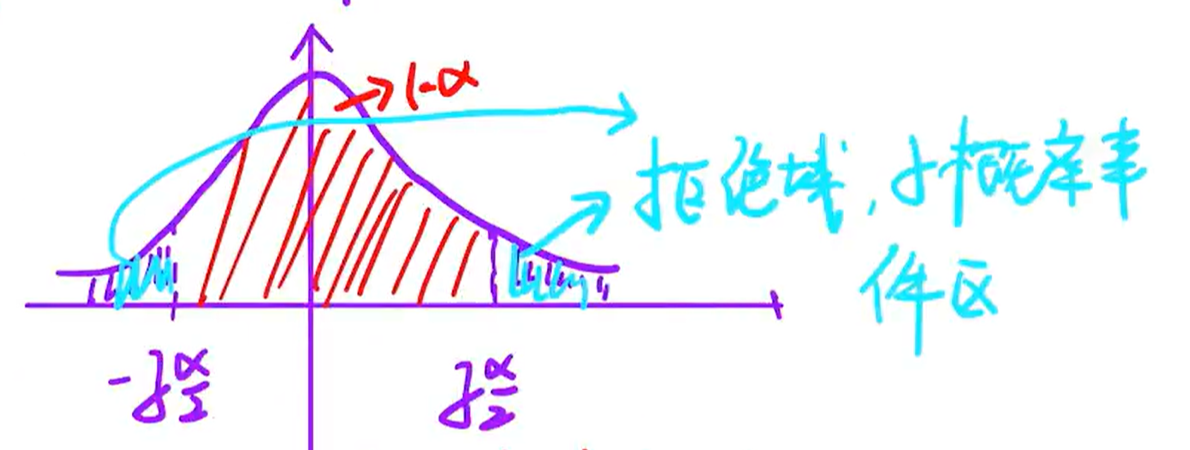 和求置信区间类似,但假设性检验是要求出上下分位点,然后对已知抽样进行判断,看是否落在置信区间内,如果是则接受原假设,否则拒绝
和求置信区间类似,但假设性检验是要求出上下分位点,然后对已知抽样进行判断,看是否落在置信区间内,如果是则接受原假设,否则拒绝