笔记内容包含常见的经典机器学习中遇到的一些概念,每个章节的内容都可独立观看,目标是对每个机器学习概念给出严谨的推导或适当的例子进行说明
极大似然估计
似然函数是用真实数据来拟合理论模型,首先要假设数据服从某一分布 ,对于真实数据 ,要满足 最大,即让真实数据在理论模型的分布下构成的概率尽可能大
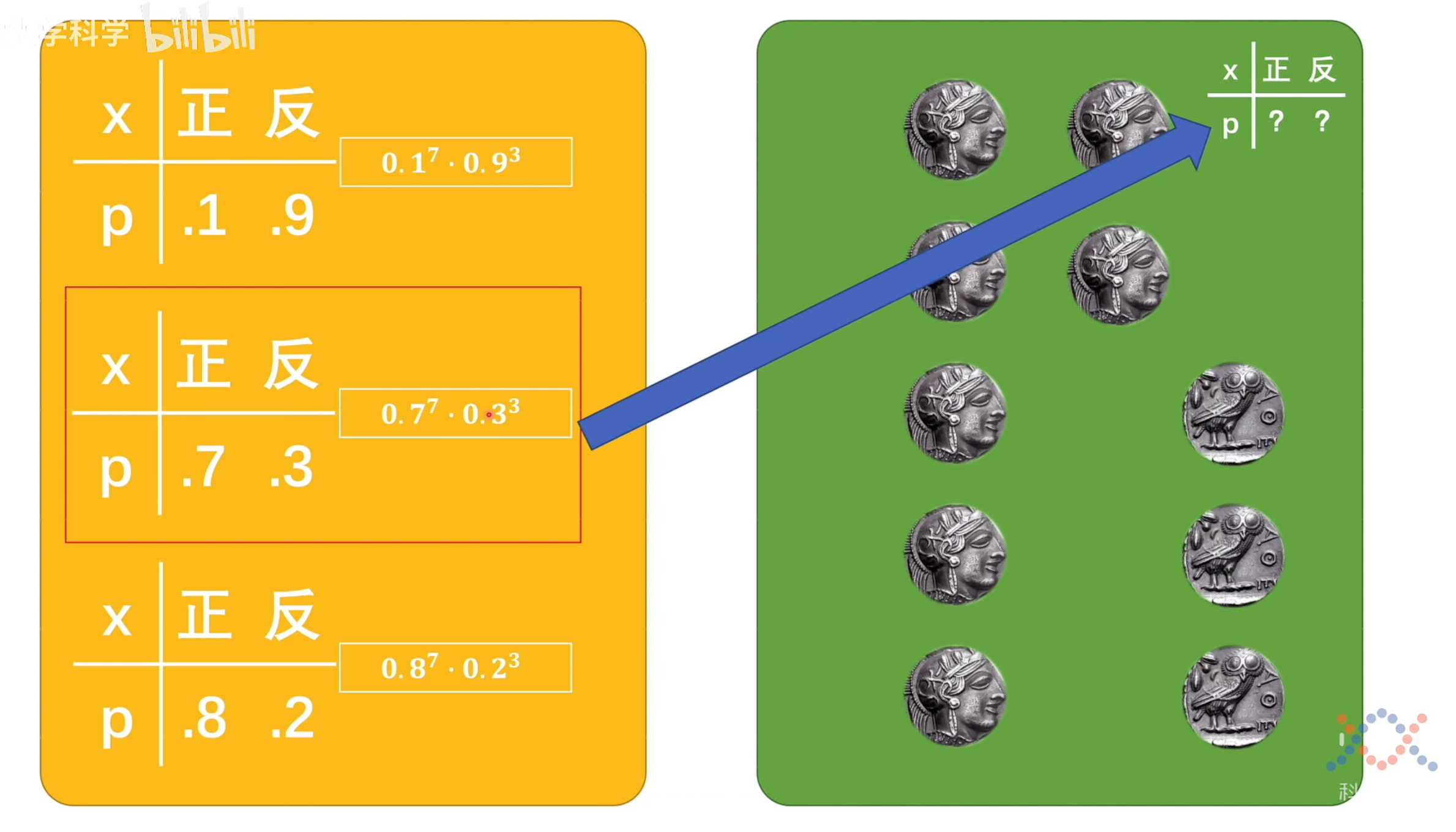
举一个扔硬币的例子,在这个例子中,左侧是理论分布,右侧是实验的真实数据,根据实验结果不能反推出理论模型;根据理论模型也不能够说明实验结果就和模型中的概率分布一样,但是我可以找到一个理论分布的参数,让真实数据的分布概率尽可能和理论分布一致,这个过程就是找似然函数的过程,求得理论分布参数的过程就是求极大似然估计的过程
Example
- 以 logistic 回归为例:
- 目标是最大化似然函数:
- 是一个从一个概率分布得到的概率, 是输入的真实数据, 代表整个神经网络的权重参数, 表示神经网络输出的概率
- 类比上述抛硬币过程,由 的标签可知, 的分布符合伯努利分布 ,因此最后的 可以被转换为 ,通过取对数 就可以求得最后要优化的损失函数为:
KL 散度
KL散度(Kullback-Leibler divergence),可以以称作相对熵(relative entropy)或信息散度(information divergence)。
KL散度的理论意义在于度量两个概率分布之间的差异程度,当KL散度越大的时候,说明两者的差异程度越大;而当KL散度小的时候,则说明两者的差异程度小。如果两者相同的话,则该KL散度应该为0。
现有两个连续随机变量 和 ,它们对于的概率密度函数分别为 和 ,如果我们用 去近似 ,则 KL 散度可以表示为:
- KL 散度的性质:
- 非负性,即
- 非对称性,即 去近似 不等于 去近似
逆变换采样
如果我有一个服从均匀分布 的随机数,怎么把这个随机数扩展到任意分布 上,并保持随机特性呢?
- 使用逆变换采样,先找到分布 的逆概率分布函数,然后将服从 的随机数带入,即可得到对应的 分布上的随机数
Summary
证明: 设分布 的概率分布函数为 , 是一个分布的随机变量,满足 ,其对应的逆概率分布函数为 ,对其随机变量进行变换就是 ,现在要证明随机变量 服从均匀分布 等式两边就是 为均匀分布的定义,因此可以证明 为均匀分布,且逆概率分布函数就是其采样函数
主成分分析(PCA 降维)
PCA 通过线性变换将原始数据转换为一组新的正交基向量,这些基向量被称为主成分。它的目标是找到方差最大的方向,使得数据在这些方向上能够最大程度地保留原始数据的信息,同时去除数据中的相关性和噪声,从而实现降维。
- 计算步骤:
- 数据标准化:对原始数据进行标准化处理,将每个特征的均值调整为 0,方差调整为 1,以消除不同特征之间在量纲和尺度上的差异。
- 计算协方差矩阵:根据标准化后的数据计算协方差矩阵,协方差矩阵可以反映各个特征之间的相关性。
- 计算特征值和特征向量:对协方差矩阵进行特征分解,得到特征值和对应的特征向量。特征值表示对应主成分的方差大小,特征向量表示主成分的方向。
- 选择主成分:按照特征值从大到小的顺序对特征值和特征向量进行排序,选择前 k 个特征向量作为主成分,其中 k 是根据实际需求和数据特点确定的降维后的维度。
- 投影数据:将原始数据投影到选择的 k 个主成分上,得到降维后的数据。
Attention
- 线性假设:PCA 假设数据是线性可分的,对于非线性数据的降维效果可能不太理想。
- 信息损失:尽管 PCA 旨在保留最大的方差,但在降维过程中仍然会不可避免地损失一些信息。
- 对异常值敏感:数据中的异常值可能会对协方差矩阵的计算产生较大影响,从而影响主成分的计算和降维效果。
线性回归
原理
- 线性回归的基本原理是通过一个或多个自变量(特征)来预测一个连续的因变量(目标),假设因变量与自变量之间存在线性关系。即通过找到一条最佳的直线(在多维空间中是超平面)来拟合数据点,使得实际观测值与预测值之间的误差最小。
模型表示
- 对于简单线性回归(只有一个自变量),其模型可以表示为:,其中y是因变量, 是自变量, 是截距, 是斜率, 是误差项,表示实际值与预测值之间的差异,通常假设 服从均值为 的正态分布。
- 对于多元线性回归(有多个自变量),模型可以表示为:,其中 是 个自变量, 是对应的参数。
求解方法
- 最小二乘法:这是线性回归中最常用的求解方法。其目标是最小化实际观测值 与预测值 之间的平方误差之和,即 。通过对 关于 求偏导数,并令偏导数为 ,可以得到一组线性方程组,求解该方程组即可得到参数 的估计值。
Example
对于一元线性回归模型 yi=β0+β1xi+ϵi,其中 i=1,2,⋯,n,yi 是观测到的因变量值,xi 是自变量值,β0 和 β1 是待估计的参数,ϵi 是误差项。
最小二乘法的目标是找到使观测值 yi 与预测值 y^i=β0+β1xi 之间的误差平方和最小的 β0 和 β1 的值,即最小化:
Q(β0,β1)=∑i=1n(yi−y^i)2=∑i=1n(yi−β0−β1xi)2
为了找到使 Q(β0,β1) 最小的 β0 和 β1,分别对 β0 和 β1 求偏导数并令其为 0。
首先对 β0 求偏导数:
∂β0∂Q=−2∑i=1n(yi−β0−β1xi)=0
化简可得:
∑i=1nyi−nβ0−β1∑i=1nxi=0
即:
β0=yˉ−β1xˉ
然后对 β1 求偏导数:
∂β1∂Q=−2∑i=1n(yi−β0−β1xi)xi=0
将 β0=yˉ−β1xˉ 代入上式并化简可得:
∑i=1n(yi−yˉ+β1xˉ−β1xi)xi=0
∑i=1n[(yi−yˉ)−β1(xi−xˉ)]xi=0
∑i=1n(yi−yˉ)xi−β1∑i=1n(xi−xˉ)xi=0
因为 ∑i=1n(xi−xˉ)xi=∑i=1n(xi−xˉ)(xi−xˉ+xˉ)=∑i=1n(xi−xˉ)2
所以可得:
β1=∑i=1n(xi−xˉ)2∑i=1n(xi−xˉ)(yi−yˉ)
这样就得到了 β1 的计算公式。
- 梯度下降法:这是一种迭代优化算法。首先随机初始化参数 ,然后根据损失函数 对 的梯度来不断更新 的值,使得 逐渐减小,直到收敛到最小值或满足一定的停止条件。在每次迭代中,参数θ的更新公式为 ,其中 是学习率,控制着参数更新的步长。
评估指标
- 均方误差(MSE):计算预测值与实际值之间误差的平方的平均值,即,MSE 的值越小,说明模型的预测效果越好。
- 平均绝对误差(MAE):计算预测值与实际值之间误差的绝对值的平均值,即,MAE 也能反映模型的预测精度,其值越小,模型性能越好。
- 决定系数(R2):用于衡量模型对数据的拟合程度,取值范围在 到 之间。 ,其中 是 的均值。R2 越接近 ,说明模型对数据的拟合效果越好;R2 越接近 ,说明模型的拟合效果越差。
逻辑回归
基本原理
逻辑回归基于线性回归模型,但通过一个非线性的逻辑函数(也称为 Sigmoid 函数)将线性回归的结果映射到一个概率值上,从而实现对分类问题的处理。Sigmoid 函数的表达式为:,它可以将任意实数映射到 区间,这个区间的数值可以被解释为属于某个类别的概率。
模型训练
给定一组训练数据 ,其中 是特征向量, 是对应的类别标签(通常取 或 )。逻辑回归模型的目标是找到一组最优的参数 ,使得模型能够尽可能准确地预测类别。这通常通过最小化损失函数来实现,常用的损失函数是对数损失函数(Log Loss),其表达式为:,其中 是模型对 的预测概率。
通过优化算法(如梯度下降法)来迭代更新参数 ,使得损失函数的值最小化,从而得到最优的模型参数。
支持向量机(SVM)
基本概念
SVM 的基本思想是在特征空间中找到一个最优超平面,将不同类别的数据点尽可能分开,并且使该超平面与各类数据点之间的间隔最大化。这个最优超平面可以用线性方程来表示,对于线性可分的数据,它能够将两类数据完全正确地分开;对于线性不可分的数据,SVM 通过引入核函数将数据映射到高维空间,使其在高维空间中变得线性可分,然后再寻找最优超平面。
关键术语
- 支持向量:是那些距离分类超平面最近的样本点,它们对确定超平面的位置和方向起着关键作用。
- 间隔:是指两类数据点到超平面的距离之和,SVM 的目标就是找到一个超平面,使得间隔最大,从而提高分类的泛化能力。
- 核函数:将低维空间中的非线性问题转化为高维空间中的线性问题的函数。常见的核函数有线性核、多项式核、高斯核(RBF 核)等。
训练过程
线性可分的 SVM 训练过程
对于线性可分的数据,SVM 的目标是找到一个最优超平面,使得间隔最大化。具体步骤如下:
- 定义优化问题:
- 假设我们有训练数据集 {(x1,y1),(x2,y2),⋯,(xn,yn)},其中 xi∈Rd 是第 i 个样本的特征向量,yi∈{−1,+1} 是对应的类别标签。
- 超平面可以表示为 wTx+b=0,其中 w 是法向量,b 是截距。
- 优化目标是最大化间隔 ∥w∥2,等价于最小化 21∥w∥2,同时满足约束条件 yi(wTxi+b)≥1 ,i=1,2,⋯,n。
- 这是一个带约束的凸二次规划问题,可以通过拉格朗日乘子法将其转化为对偶问题进行求解。
- 引入拉格朗日乘子:
- 构造拉格朗日函数 L(w,b,α)=21∥w∥2−∑i=1nαi(yi(wTxi+b)−1),其中 αi≥0 是拉格朗日乘子。
- 对 w 和 b 求偏导数并令其为 0,得到:
- ∂w∂L=w−∑i=1nαiyixi=0,即 w=∑i=1nαiyixi。
- ∂b∂L=−∑i=1nαiyi=0。
- 将上述结果代入拉格朗日函数,得到对偶问题:
- 最大化 ∑i=1nαi−21∑i=1n∑j=1nαiαjyiyjxiTxj。
- 约束条件为 ∑i=1nαiyi=0,αi≥0,i=1,2,⋯,n。
- 求解对偶问题:
- 可以使用序列最小优化(SMO)算法等方法求解对偶问题,得到最优的拉格朗日乘子 α∗。
- 计算 w 和 b:
- 根据 w=∑i=1nαi∗yixi 计算 w∗。
- 选择一个支持向量(即 αj∗>0 的样本点 (xj,yj)),根据 yj(w∗Txj+b∗)=1 计算 b∗。
线性不可分的 SVM 训练过程
对于线性不可分的数据,需要引入松弛变量 ξi 来允许一些样本点违反间隔约束。具体步骤如下:
- 定义优化问题: 优化目标是最小化 21∥w∥2+C∑i=1nξi,其中 C>0 是惩罚参数,用于控制对误分类样本的惩罚程度。 约束条件为 yi(wTxi+b)≥1−ξi,ξi≥0,i=1,2,⋯,n。
- 引入拉格朗日乘子: 构造拉格朗日函数 L(w,b,ξ,α,μ)=21∥w∥2+C∑i=1nξi−∑i=1nαi(yi(wTxi+b)−1+ξi)−∑i=1nμiξi,其中 αi≥0,μi≥0 是拉格朗日乘子。 对 w、b 和 ξ 求偏导数并令其为 0,得到: ∂w∂L=w−∑i=1nαiyixi=0,即 w=∑i=1nαiyixi。 ∂b∂L=−∑i=1nαiyi=0。 ∂ξi∂L=C−αi−μi=0。 将上述结果代入拉格朗日函数,得到对偶问题: 最大化 ∑i=1nαi−21∑i=1n∑j=1nαiαjyiyjxiTxj。 约束条件为 ∑i=1nαiyi=0,0≤αi≤C,i=1,2,⋯,n。
- 求解对偶问题: 同样可以使用 SMO 算法等方法求解对偶问题,得到最优的拉格朗日乘子 α∗。
- 计算 w 和 b: 根据 w=∑i=1nαi∗yixi 计算 w∗。 选择一个支持向量(即 0<αj∗<C 的样本点 (xj,yj)),根据 yj(w∗Txj+b∗)=1 计算 b∗。
最近邻居(KNN)
算法原理
存在一个样本数据集合,也称为训练数据集,其中每个数据都有对应的类别或数值标签。当新的未知数据到来时,KNN 算法会计算这个新数据与训练数据集中所有数据的距离(通常使用欧氏距离、曼哈顿距离等),然后找出距离最近的 K 个数据点。根据这 K 个近邻数据点的类别或数值情况来决定新数据的类别或数值。如果是分类问题,通常采用投票法,即看这 K 个近邻中哪种类别出现的次数最多,就将新数据归为该类别;如果是回归问题,则一般采用平均法,将这 K 个近邻的数值求平均作为新数据的预测值。
求解过程
距离计算
距离计算是 KNN 算法的核心步骤之一,用于衡量新数据点与训练数据集中各点的相似度。常见的距离度量公式有以下几种:
欧氏距离(Euclidean Distance)
欧氏距离是最常用的距离度量方式,用于计算 n 维空间中两点之间的直线距离。对于两个 n 维向量 x=(x1,x2,⋯,xn) 和 y=(y1,y2,⋯,yn),它们之间的欧氏距离 d(x,y) 计算公式为:
d(x,y)=∑i=1n(xi−yi)2
曼哈顿距离 (Manhattan Distance)
曼哈顿距离也称为城市街区距离,它是指在城市街区中,从一个点到另一个点沿着网格线行走的最短距离。对于两个 n 维向量 x=(x1,x2,⋯,xn) 和 y=(y1,y2,⋯,yn),它们之间的曼哈顿距离 d(x,y) 计算公式为:
d(x,y)=∑i=1n∣xi−yi∣
闵可夫斯基距离 (Minkowski Distance)
闵可夫斯基距离是欧氏距离和曼哈顿距离的一般形式,对于两个 n 维向量 x=(x1,x2,⋯,xn) 和 y=(y1,y2,⋯,yn),以及一个参数 p,它们之间的闵可夫斯基距离 d(x,y) 计算公式为:
d(x,y)=(∑i=1n∣xi−yi∣p)p1
当 p=2 时,闵可夫斯基距离就是欧氏距离;当 p=1 时,闵可夫斯基距离就是曼哈顿距离。
分类或回归决策
分类问题 (投票法)
在分类问题中,当确定了新数据点的 K 个最近邻后,通常采用投票法来决定新数据点的类别。假设 K 个最近邻中属于类别 cj 的样本数量为 nj,其中 j=1,2,⋯,m,m 为类别总数。则新数据点的类别 C 为:
C=argmaxjnj
即选择出现次数最多的类别作为新数据点的类别。
回归问题 (平均法)
在回归问题中,当确定了新数据点的 K 个最近邻后,通常采用平均法来预测新数据点的数值。假设 K 个最近邻的数值分别为 y1,y2,⋯,yK,则新数据点的预测值 y^ 为:
y^=K1∑i=1Kyi
K 均值(K-Means)
算法原理
给定一个包含 n 个数据点的数据集,以及要划分的簇数 k,k - means 算法的目标是将这些数据点划分为 k 个簇,使得每个簇内的数据点尽可能相似,而不同簇之间的数据点尽可能不同。它通过迭代计算每个数据点到各个簇中心的距离,将数据点分配到距离最近的簇中,并不断更新簇中心,直到簇中心不再发生变化或达到预设的迭代次数。
算法步骤
- 初始化簇中心:随机选择 k 个数据点作为初始的簇中心。
- 分配数据点到簇:对于数据集中的每个数据点,计算它与 k 个簇中心的距离,将其分配到距离最近的簇中。
- 更新簇中心:对于每个簇,计算该簇内所有数据点的均值,将其作为新的簇中心。
- 重复步骤 2 和 3:不断重复分配数据点到簇和更新簇中心的步骤,直到簇中心不再发生变化,或者达到预设的迭代次数。
贝叶斯模型
朴素贝叶斯
- 参考资料:
- 《统计学习方法第 2 版》——李航
从统计角度分析,对于给定数据 和标签 预测任务相当于计算 ,将该概率公式用条件概率公式展开可得:
因此 的计算变成了估算 和 ,使用贝叶斯公式可得:
在计算分类时,所有的分类都包含 ,直接可以省略,只需计算
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | |
| S | M | M | S | S | S | M | M | L | L | L | M | M | L | L | |
| -1 | -1 | 1 | 1 | -1 | -1 | -1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | -1 |
Example
根据上表,计算下列概率
对于数据 可得出(注意,这里假设 独立同分布):
- 根据两个概率可以得出,应该预测分类为
动态贝叶斯
决策树
- 参考资料:
- 《统计学习方法第 2 版》—— 李航
- 数据挖掘技术课程

决策树由节点和有向边组成,节点分为内部节点和叶子节点,内部节点表示划分属性,叶子节点是最后的分类结果
下图是决策树算法的主要内容:
信息增益
假设有一组数据,有 n 个不同的属性特征,对任意一个特征 有以下分析:
- 熵的概念 设 X 为一个取有限值的离散随机变量,对整个系统的熵为:,熵越大,随机变量的不确定性就越大,公式中的 表示取离散值 的概率
- 条件熵的概念 条件熵 表示在已知随机变量 的条件下,随机变量 的不确定性
信息增益表示得知特征 的信息而使类 的信息不确定性减少的程度
- 信息增益的定义: 特征 对训练数据集 的信息增益 ,定义为集合 的经验熵 与特征 给定条件下 的经验条件熵 之差,即
Note
上文的“经验”指的是通过统计结果计算熵和条件熵,其思想是极大似然估计
Example
- 计算标签类别的经验熵,熵越小表示数据越稳定:
- 设年龄、有工作、有自己的房子、信贷情况为特征 ,分别计算它们的经验条件熵和信息增益
- 从上面的计算来看,特征 最合适用来划分数据,因此根据特征 可以划分为三个子集(一般,好,非常好),并在三个子集上重复进行计算,直到满足停止条件
信息增益比
信息增益偏向于生成分支较多的树,因为分支越多,它的条件熵就可能越低 (越稳定)
为了修正这个问题,我们需要使用信息增益比:
其中 表示特征 的经验熵(有点像对信息增益做了一次标准化),
基尼指数
适用于分类树的生成,能够决定改特征的最优二值切分点
分类问题中,假设有 个类,样本点属于第 类的概率为 ,则概率分布的基尼指数定义为
即,进行两次独立抽样两次都不同的概率,它能够反映数据集中类别分布的分散程度。对于二分类问题,可简化为
基尼指数和熵的概念有异曲同工之妙,当划分的类概率为 时,与其不是 的概率 对系统的熵为 ,基尼指数的表示更加简单,但也反映了所包含的信息量
对于给定样本的集合 ,其基尼指数为
在特征 的条件下,集合 的基尼指数定义为
剪枝算法
剪枝算法=损失函数+正则化惩罚项
设树 T 的叶结点个数为 , 是树 的叶结点,该叶结点有 个样本点,其中 类的样本点有 个,, 为叶结点 上的经验熵, 为参数,则决策树学习的损失函数可以定义为:
其中经验熵为:
如果将第一项记为 ,则公式可以简化为:
Note
算法步骤:
- 计算每个节点的经验熵
- 递归地从叶节点向上回缩 比较回缩 与不回缩 的剪枝损失,然后进行比较 如果 ,则进行剪枝操作
- 重复步骤 2,直到不能继续为止
Attention
优点:可以从结构上简化决策树,提高泛化能力 缺点:简化决策树容易造成欠拟合,不能保证划分准确性的提升
在进行剪枝时,我们可以利用数据集的验证集,进行预剪枝/后剪枝
- 预剪枝:预剪枝就是在构造决策树的过程中,先对每个结点在划分前进行估计,若果当前结点的划分不能带来决策树模型泛化性能的提升,则不对当前结点进行划分并且将当前结点标记为叶结点
- 后剪枝:后剪枝就是先把整颗决策树构造完毕,然后自底向上的对非叶结点进行考察,若将该结点对应的子树换为叶结点能够带来泛化性能的提升,则把该子树替换为叶结点
最小二乘回归树
假设已将输入的特征空间划分为 个单元 ,并且在每个单元 上有一个固定的输出值 ,于是回归树模型可以表示为
其中 为指示函数,上面的式子表示输入 x 在回归树的划分 下最终有一个唯一的输出
我们使用平方误差 来表示回归树对于训练数据的预测误差,我们的目标是 ,并取
| 看电视时长 | 婚姻状况 | 职业 | 年龄 |
|---|---|---|---|
| 3 | 未婚 | 学生 | 12 |
| 4 | 未婚 | 学生 | 18 |
| 2 | 已婚 | 老师 | 26 |
| 5 | 已婚 | 上班族 | 47 |
| 2.5 | 已婚 | 上班族 | 36 |
| 3.5 | 未婚 | 老师 | 29 |
| 4 | 已婚 | 学生 | 21 |
Example
下面我们将利用上面的数据对年龄进行预测 首先将 的属性选为职业,则有三种划分情况{“老师”,“学生”}、{“上班族”}以及{“老师”,“上班族”}、{“学生”},最后一种为{“学生”,“上班族”}、{“老师”}
- 第一种情况 R1={“学生”},R2={“老师”,“上班族”} 最小平方误差为:
- R1={“老师”},R2={“学生”,“上班族”} 最小平方误差为:
- 划分情况为 R1={“上班族”},R2={“学生”,“老师”} 最小平方误差为:
由上面的分析可知,应该选择第三种划分
CART
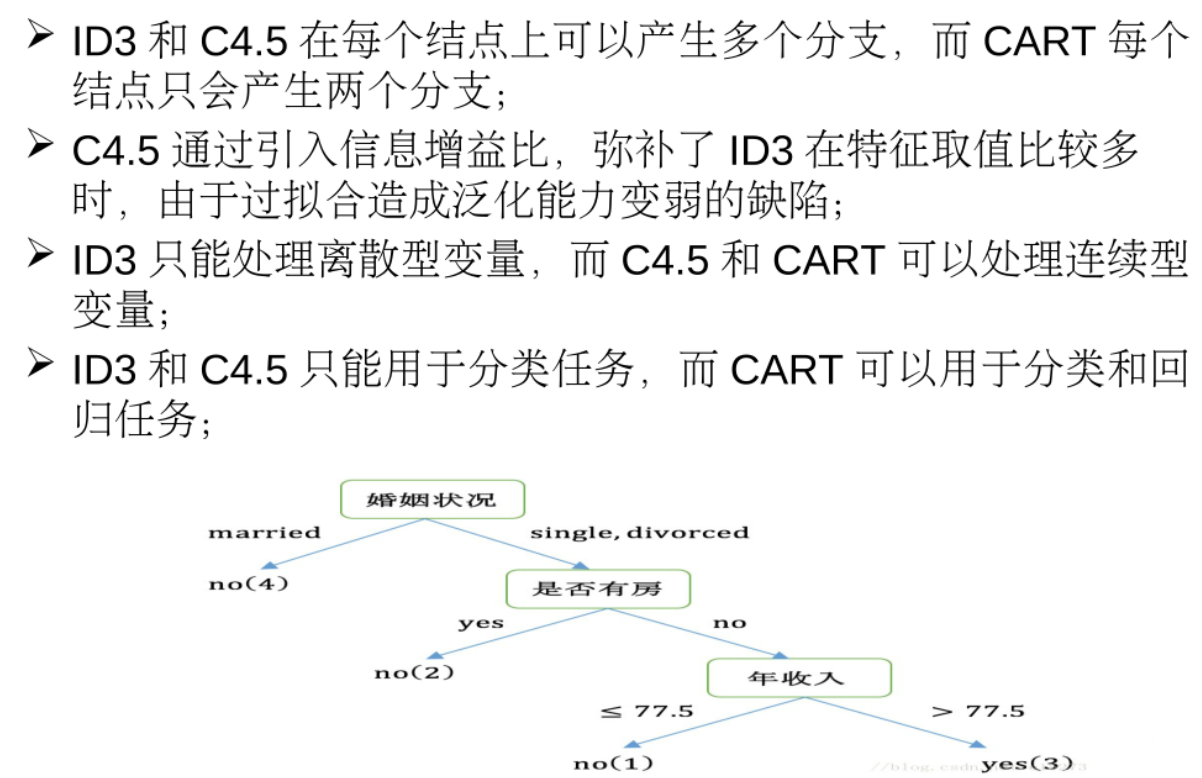
ID3 和 C4.5 都是基于信息增益的方法,适用于离散特征的分类,不再赘述
CART 生成算法和最小二乘法回归树方法差不多,分别计算出每个特征的最优切分点,然后找到最优特征的最优切分点作为划分的分支
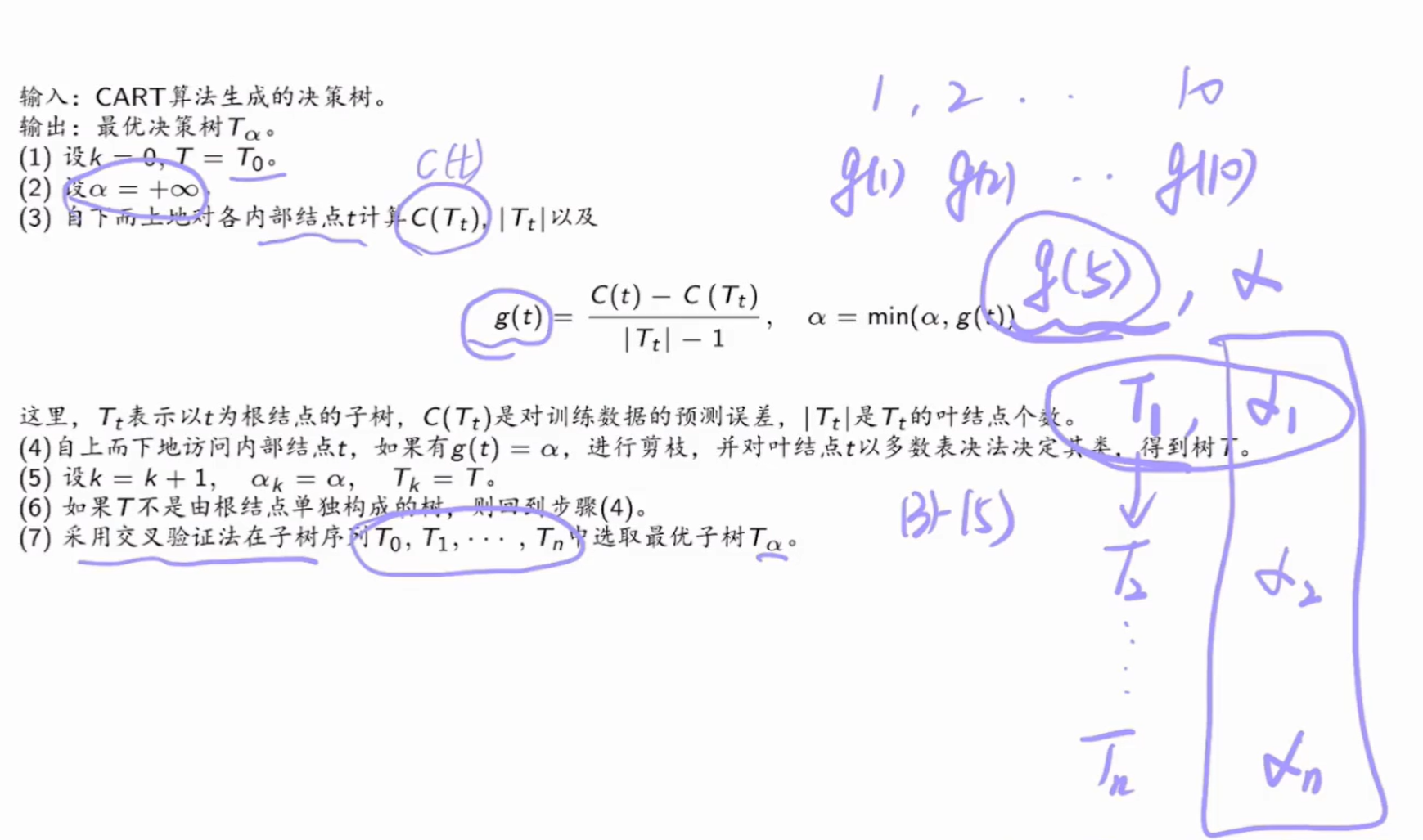
在决策树的剪枝算法 中,我们需要考虑代价 和复杂度 两个因素,如果取 就是一棵完整的树,如果取 则是一个单结点树,因此 的取值十分重要,在 CART 中,考虑以下情况:
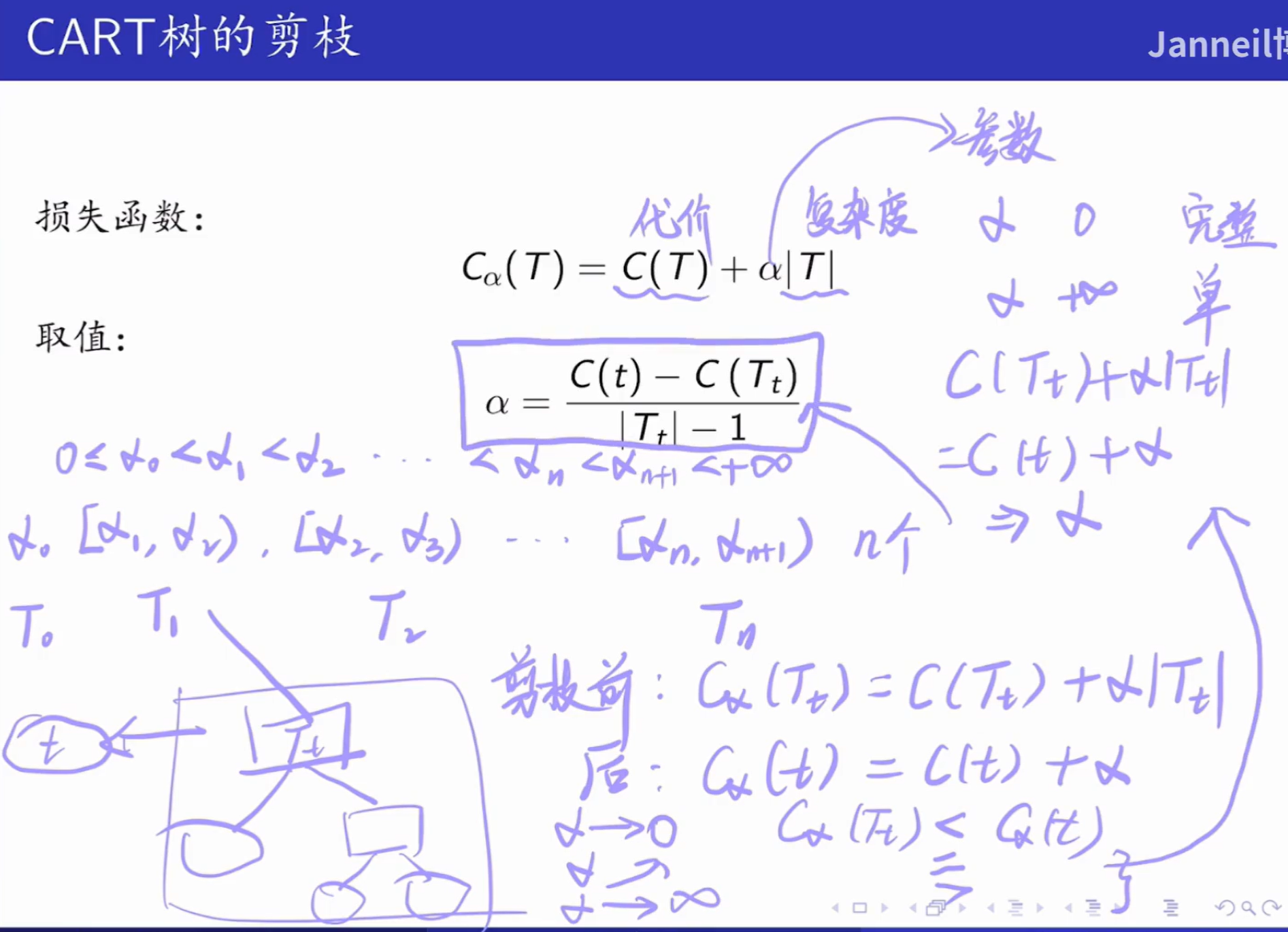
取 ,其中每一个 都是一个临界值,每个范围 都表示一个树
假如树 T 存在一个子树 ,则
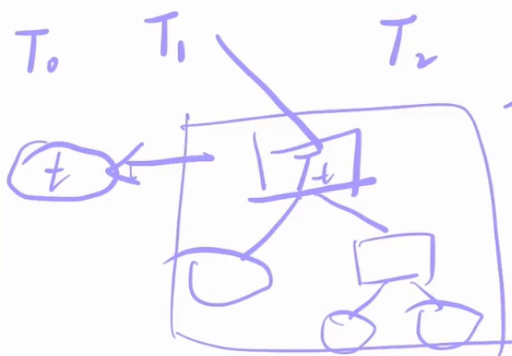
- 剪枝前损失函数为:
- 剪枝后损失函数为: (剪枝后只有一个叶子节点) 存在临界点使得 ,如果 再大一点,剪枝后损失函数的损失值就会小于剪枝前,偏向于进行剪枝,求出这个 临界值就是公式
Summary
从上面的剪枝过程可以看出, 是有嵌套关系的,后者是前者的子树,在搞清楚 的取值过程后,我们需要利用公式求得最优决策树
随机森林
基本原理
随机森林通过集成多个决策树来进行分类、回归等任务。它从训练数据集中有放回地随机抽样,构建多个决策树,然后综合这些决策树的结果来做出最终决策。由于每棵树的构建都基于不同的样本子集和特征子集,因此随机森林能够有效降低模型的方差,提高模型的泛化能力,减少过拟合的风险。
算法步骤
- 数据抽样:从原始训练数据集 D 中有放回地随机抽取 n 个样本,组成一个新的训练子集 Di。重复这个过程,得到 m 个不同的训练子集。
- 特征抽样:对于每个训练子集 Di,从原始特征集 F 中随机选择 k 个特征,作为该子集构建决策树时使用的特征集合 Fi。通常,k 的取值远小于原始特征的数量。
- 构建决策树:使用每个训练子集 Di 和对应的特征集合 Fi,分别构建一棵决策树 Ti。在构建决策树的过程中,不进行剪枝操作,让决策树尽量生长。
- 集成预测:将待预测的数据样本输入到构建好的 m 棵决策树中,得到 m 个预测结果。对于分类任务,通常采用投票法,选择出现次数最多的类别作为最终预测结果;对于回归任务,则采用平均法,将 m 个预测值的平均值作为最终预测结果。