数值稳定性

Quote

# 数值稳定性 + 模型初始化和激活函数

问题描述

在深度学习中，数值的稳定性会直接影响模型的性能，梯度的爆炸或消失会导致模型无法从数据中学习到有效的信息，尤其是在深层神经网络的前向传播和反向梯度更新的时候…

以 MLP 为例

MLP 一次前向传播可以被表示为：$f_t({\mathbf{h}}^{t-1})=\sigma ({\mathbf{W}}^t{\mathbf{h}}^{t-1})$，对其求导后可得：$\frac{\partial {\mathbf{h}}^{\prime }}{\partial {\mathbf{h}}^{t-1}}=\mathrm{diag}\left({\sigma }^{\prime }({\mathbf{W}}^{\prime }{\mathbf{h}}^{t-1})\right)(W^{\prime }{)}^T$，多层 MLP 前向传播可以被表示为 ${\prod }_{i=t}^{d-1}\frac{\partial {\mathrm{h}}^{i+1}}{\partial {\mathrm{h}}^i}={\prod }_{i=t}^{d-1}\mathrm{diag}\left({\sigma }^{\prime }(W^i{\mathrm{h}}^{i-1})\right)(W^i{)}^T$，如果 $d$ 很大，则会导致计算多个乘法

同时，激活函数在特定输入区间也可能会导致梯度消失的问题，例如这里的 sigmoid 函数：

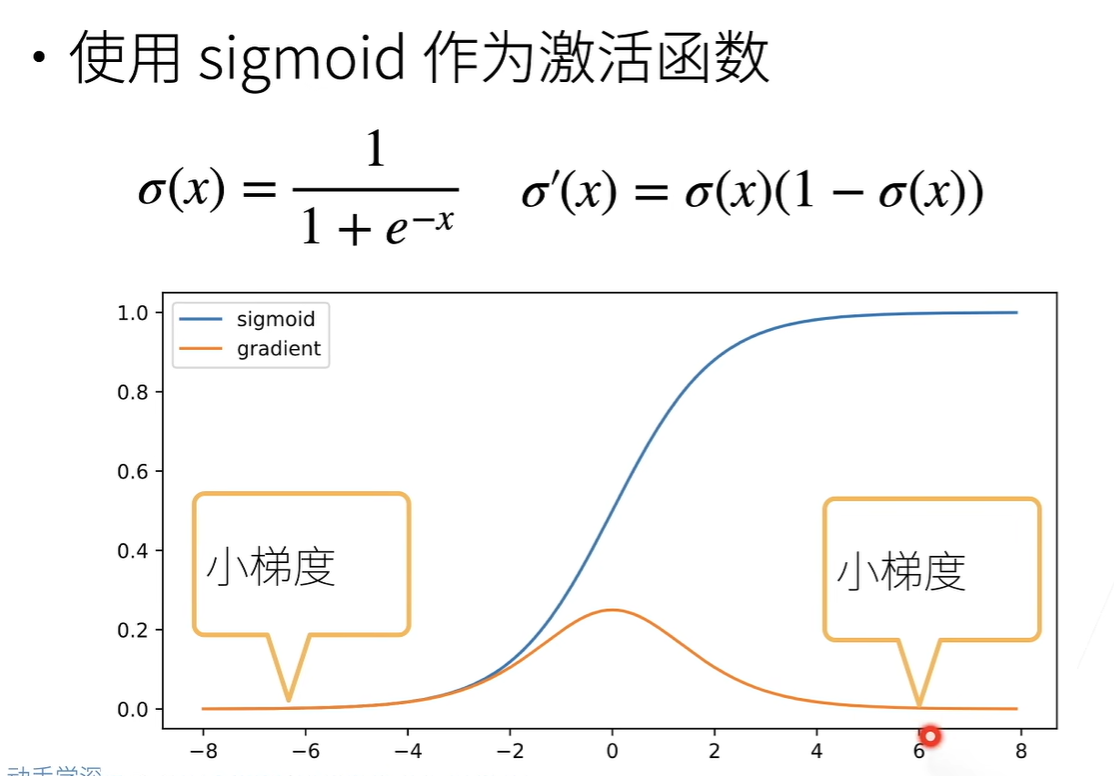
Attention

• 后向传播类似，梯度的爆炸/消失会导致模型难以训练：
• 值超出表示范围
  • 对于 16 位浮点数尤为严重（数值区间 $6e^{-5}-6e^4$)
• 对学习率敏感
  • 学习率太大 $\to$ 大参数值 $\to$ 更大的梯度
  • 学习率太小 $\to$ 训练无进展
  • 更深的网络效果没有提升

解决方案

为了解决深度学习中出现的数值稳定性问题，让训练过程更加稳定，有以下几种方案：

• 目标：让梯度值在合理的范围内
  • 例如：$1e^{-6}$, $1e^3$
• 将乘法变加法
  • ResNet, LSTM
• 归一化
  • 梯度归一化，梯度裁剪
• 合理的权重初始和激活函数

参数初始化

• 为了能够保留输入和参数的统计性质，我们提出了以下两个条件：
  1. 将每层输出和梯度都看作随机变量
  2. 让它们的均值和方差都保持一致（前向和反向期望为 $0$，方差为常数 $a$ 和 $b$）

对于小网络来说，可能一个标准正态分布的初始化参数就能有好的效果，但这并不能保证数值的稳定性

• 假设：
  • $w_{i,j}^t$ 是 $i.i.d$，那么 $\mathbb{E}[W_{i,j}^t]=0$, $\mathrm{Var}[w_{i,j}^t]={\gamma }_t$
• $h_i^{t-1}$ 独立于 $w_{i,j}^t$
• 假设没有激活函数 $h^t=W^t{h}^{t-1}$，这里 ${\mathbf{W}}^t\in {\mathbb{R}}^{n_t\times n_{t-1}}$

$$\mathbb{E}[h_i^t]=\mathbb{E}\left[\sum _j{w}_{i,j}^t{h}_j^{t-1}\right]=\sum _j\mathbb{E}[w_{i,j}^t]\mathbb{E}[h_j^{t-1}]=0$$

前向方差和反向方差证明过程如下图所示：

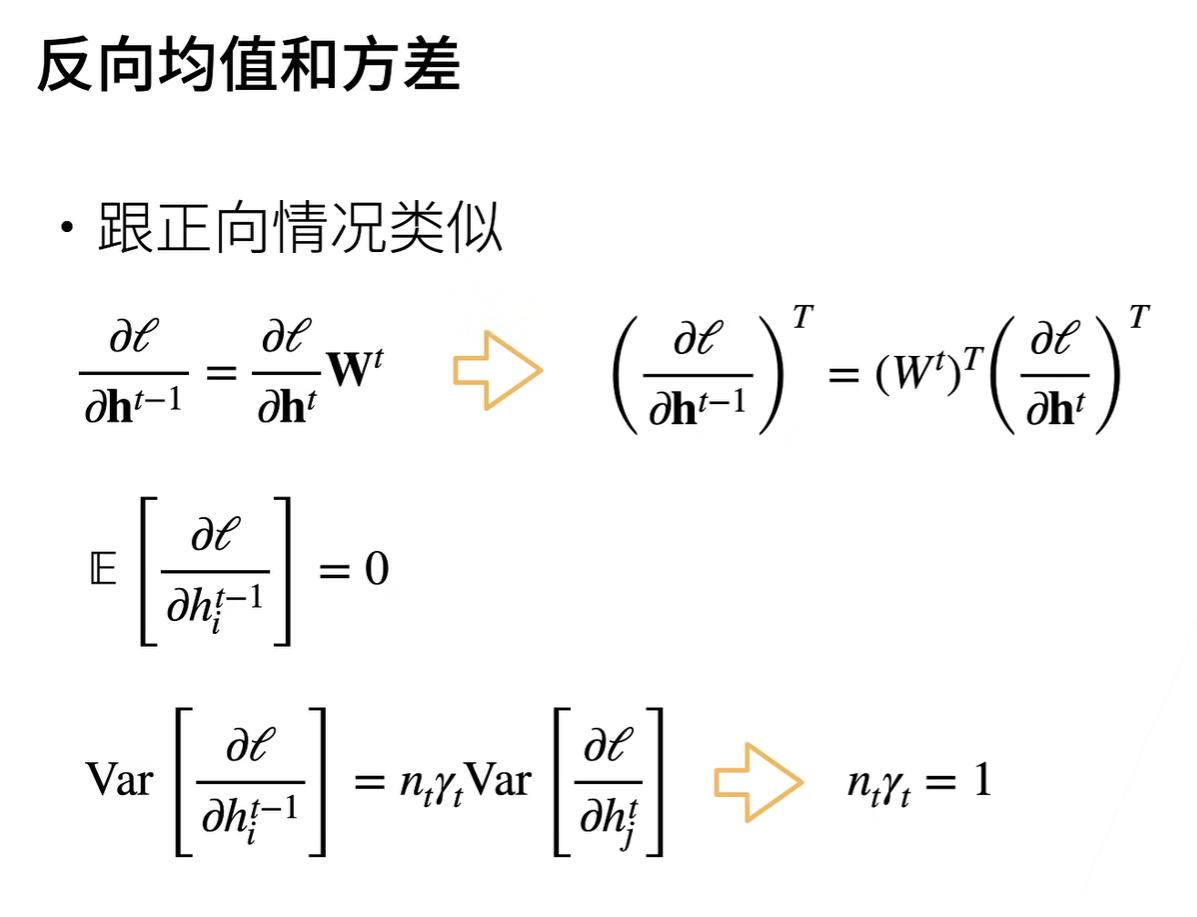
Important

• 看起来内容很多，总结下来只有三点：
  1. 正向需要满足 $n_{t-1}{\gamma }_t=1$
  2. 反向需要满足 $n_t{\gamma }_t=1$
  3. 激活函数需要近似 $f(x)=x$
• 其中，$n_{t-1}$ 表示第 $t$ 层的输入维度，$n_t$ 表示第 $t$ 层的输出维度，${\gamma }_t$ 为第 $t$ 层模型参数的常数方差
• 由于当输入维度和输出维度都相等时，就可以保证数值在训练过程中的稳定性

Xavier 初始化

由于同时满足 $n_{t-1}{\gamma }_t=1$ 和 $n_t{\gamma }_t=1$ 较为困难，因此折中一下，取一半…

pytorch 中被描述为如下图所示，gain 表示激活函数的偏差：

Kaiming 初始化

Kaiming 初始化的方法与上面类似，不过 Kaiming 只考虑输入维度或只考虑输出维度