Chapter 2 插值法
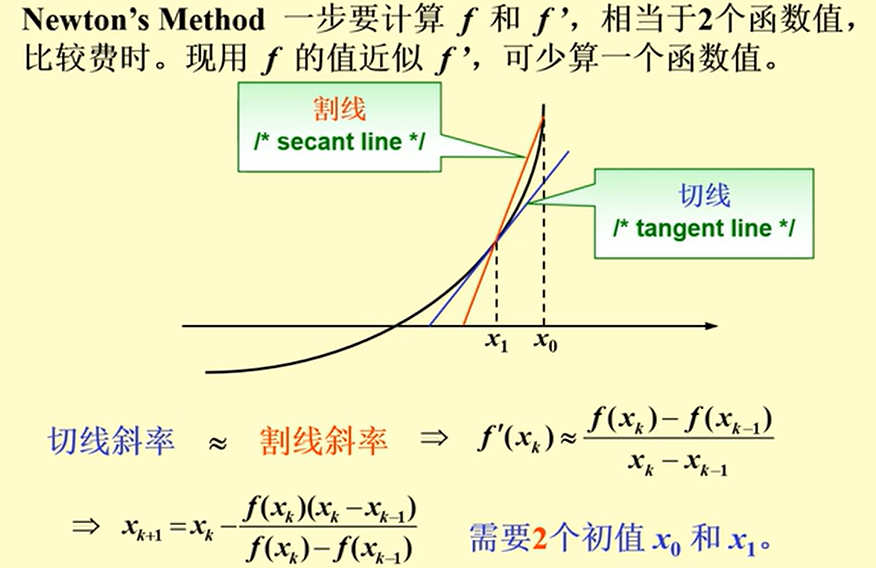
牛顿插值法
2.3 差商与牛顿插值 & 2.4 差分_哔哩哔哩_bilibili
差分

- 为什么叫向前向后差分呢?
- 向前:相对于向前的差值
- 向后:相对于向前的差值
Chapter 5. 常微分方程初值问题的数值方法
一阶常微分方程的初值问题

考虑满足唯一解的情况
需要实现的目标:

通过一系列的节点,求出精确值的近似值
基本思想
将求解区间和节点离散化

注:为了方便表示,取定步长,但是如果是非定步长也能计算,方法一样
一个例子

已知信息:
- 初值
- 函数的表示形式
具体计算方法如下:

计算方法
1. 欧拉方法
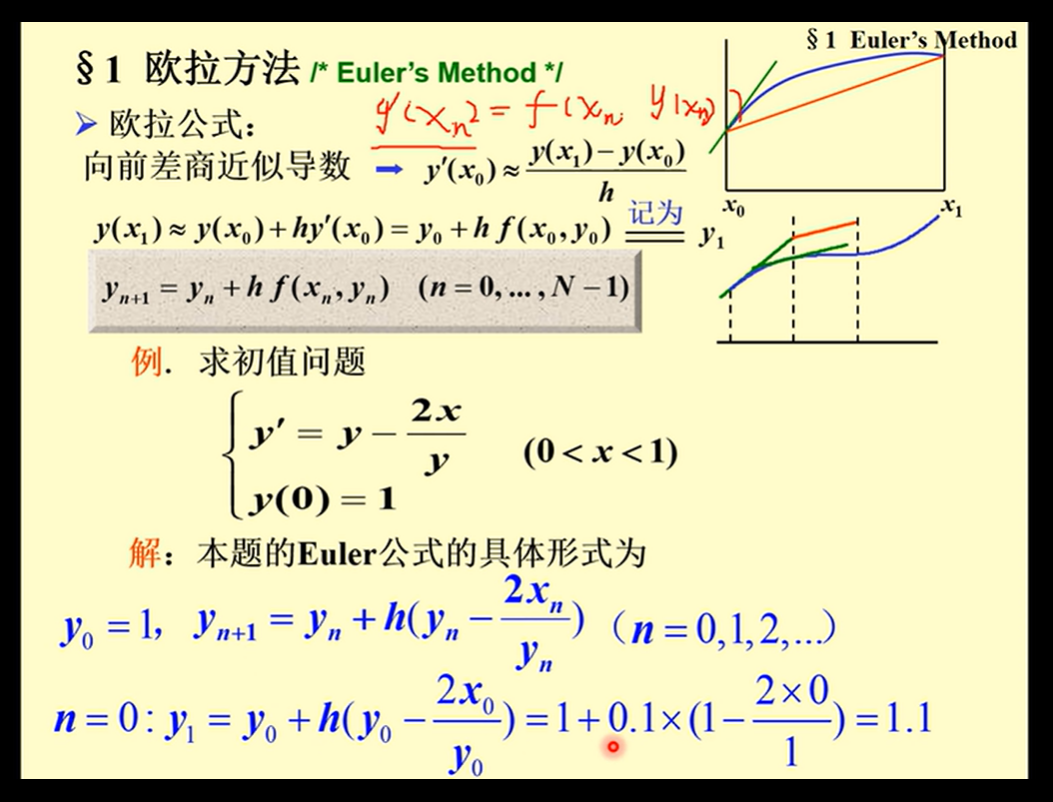
基本思想:使用向前差商近似导数,从而替换导数,得到迭代公式
欧拉公式(又称为矩形公式)
如果取近似,则称为隐式 Euler 公式
截断误差
缺点:矩形公式的精确度很低
2. 梯形公式
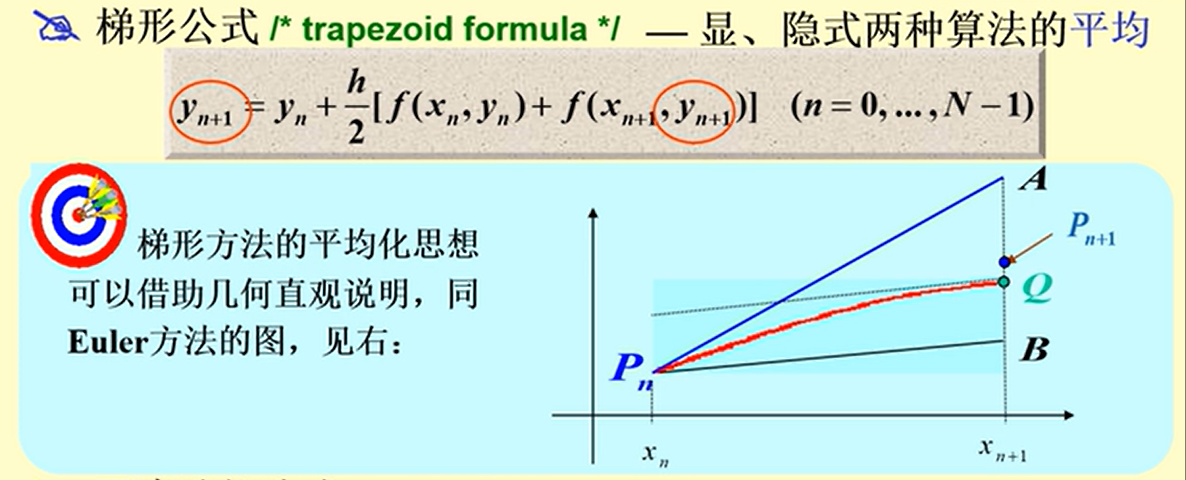
梯形公式
显式欧拉和隐式欧拉的平均计算方法
优点:精度高;缺点:计算复杂,因为含有隐式方程,不容易求解
3. 改进的欧拉公式

预测:
校正:
这种方式又叫做两步法,前面的都是单步
局部截断误差与阶


总结:
- 欧拉法具有 1 阶精度
- 改进的欧拉公式具有 2 阶精度
龙格-库塔方法

基本思想:使用微分中值定理,通过某一斜率,沿直线从


总结:
其实就是在欧拉的基础上,进行加权平均,尽可能的找更多的点近似
4 阶经典,需要记忆!!!

Chapter 6. 线性方程组的直接解法
复习 5 章 & 6 线性代数方程组的解法_哔哩哔哩_bilibili

两种数值解法

直接解法
经过算术运算,可以求得精确的方程解(如果没有舍入误差的话)
- 优点:可以在不损失精度条件下,求得低阶稠密方程组
- 缺点:高阶计算复杂,不适合求解
迭代法
通过极限过程不断逼近线性方程组的精确解
- 优点:适合解大型的稀疏方程组
- 缺点:需要不断迭代,且更加复杂(有各种精度、误差问题)
向量范数

常见范数

- -范数
- 1-范数
- 2-范数(欧式距离)
- p-范数
向量序列与向量关系

类比于数列,向量序列就是向量组成的数列
矩阵范数
6.1 引言 & 6.2 高斯消去法_哔哩哔哩_bilibili

注:相容性代表的是两个向量之间的夹角关系,其实也代表了两个向量的相似度
常用矩阵范数

-
Frobenius 范数:相当于对向量 L2 范数的推广
-
算子范数:一种更一般的形式,表示在所有向量 p-范数中,取最大的
- 行和范数
- 列和范数
- 谱范数
-
谱半径

一些没那么重要的定理

重要定理证明

结论(2)可以用来进行范数估计
高斯消元法
只考虑非奇异矩阵
基本思路
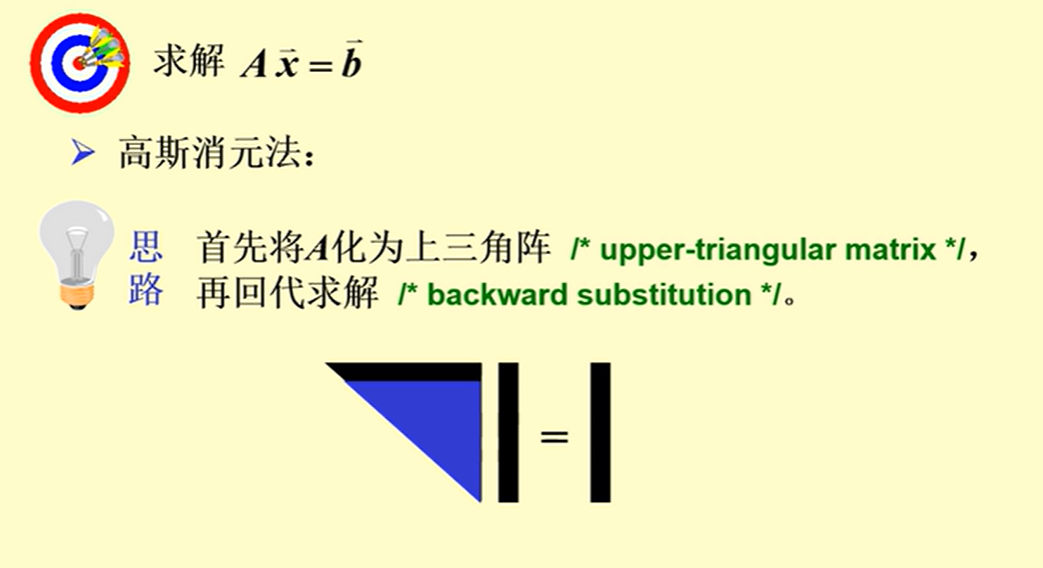
- 化为上三角阵
- 从最底层回代,因此解出
误差分析
在计算机中会出现舍入误差,为了避免分母过小,分子太大导致的计算误差,我们可以在开始运算前对矩阵做等价变换
选主元消去法
6.3 高斯主元消去法 & 6.4 矩阵分解_哔哩哔哩_bilibili
列主元消去法
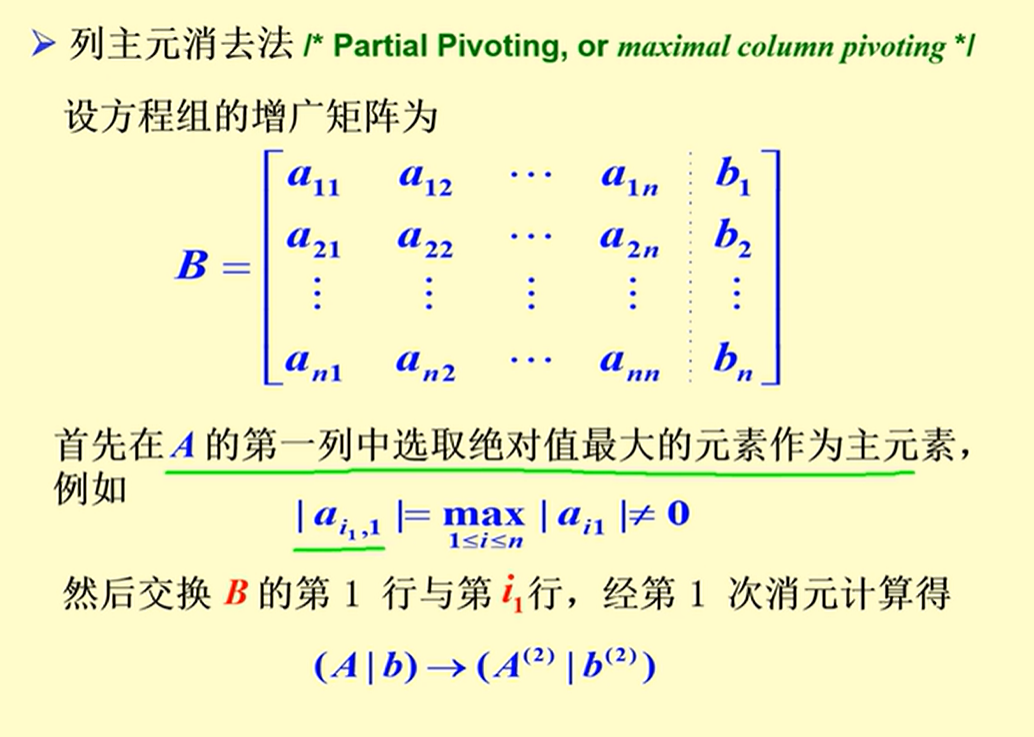
- 选取方法: 选取主列中绝对值最大的数作为除数
三角分解法
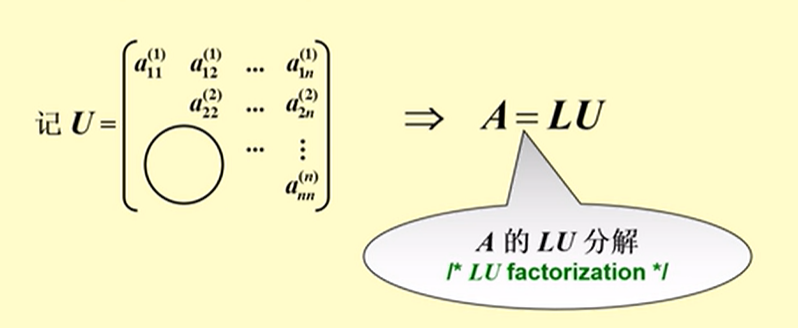
对于任意一个顺序主子式不为零的矩阵,都有这种 LU 分解
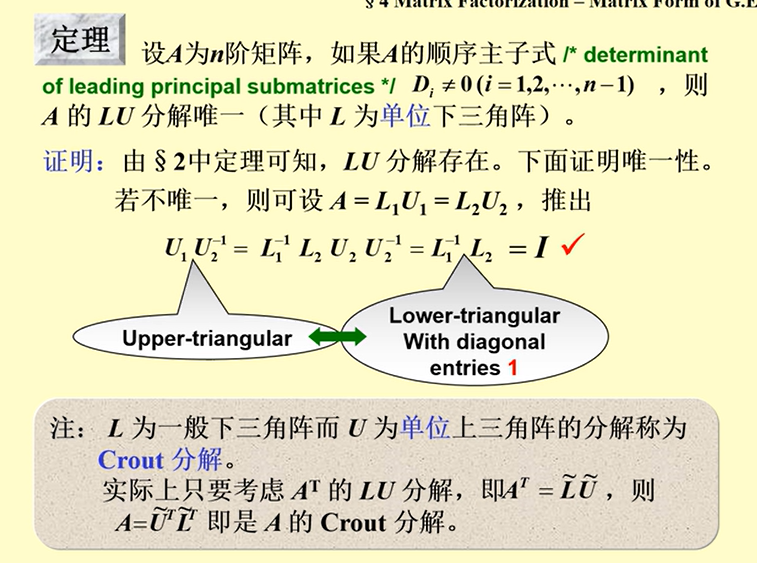
如果上三角矩阵为单位上三角矩阵,就称为 Crout 分解,只需要考虑的 LU 分解即可
当然,如果使用列主元法对三角分解进行优化也可以,不过要注意同时替换常数
误差分析
- 假设精确,由于的误差导致的误差:

- 假设精确,由于的误差导致的误差:
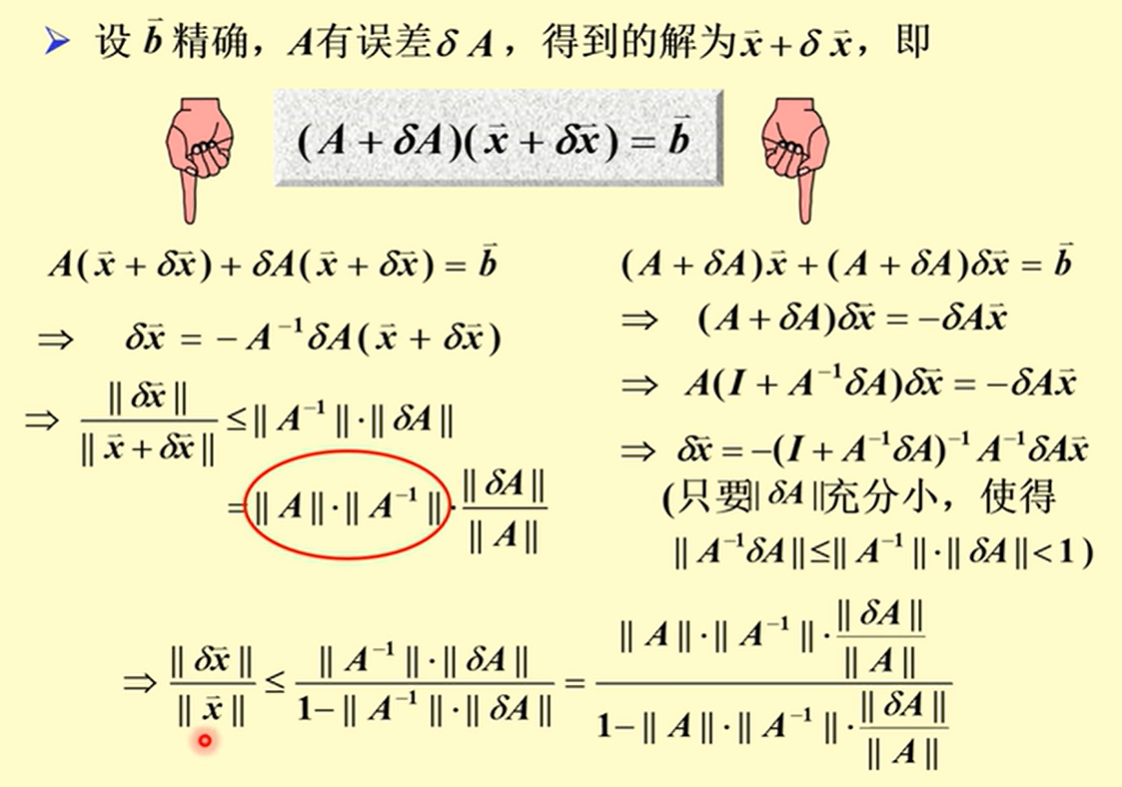

通过分析可以看出,是放大因子,如果越病态,则越难求得准确解

一些判断的经验

线性代数方程组的迭代解法
基本思想

通过对原式进行改写,得到迭代公式:,其中,,为向量,被称为迭代矩阵
- 优点:计算精度可控,适合求解系数为大型稀疏矩阵的方程组
因此要考虑如下几个问题:
- 如何建立迭代格式
- 如何才能保证迭代公式收敛?
- 收敛速度多少?
- 误差估计
Jacobi 迭代法
6.6.1 迭代公式 & 6.6.2 迭代法收敛性_哔哩哔哩_bilibili
一个例子

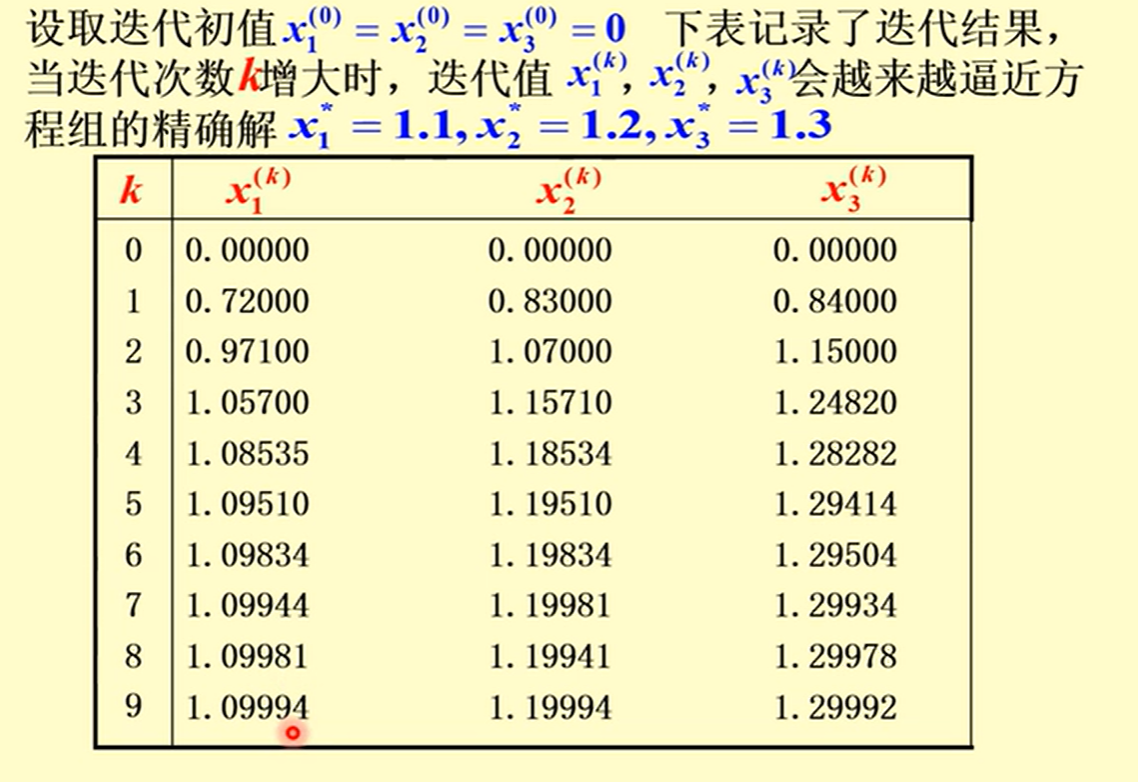 这个例子告诉我们,解线性方程组的迭代法,其基本思想是将联立方程组的求解归结为重复计算一组彼此独立的线性表达式
这个例子告诉我们,解线性方程组的迭代法,其基本思想是将联立方程组的求解归结为重复计算一组彼此独立的线性表达式
Jacobi 迭代的矩阵形式
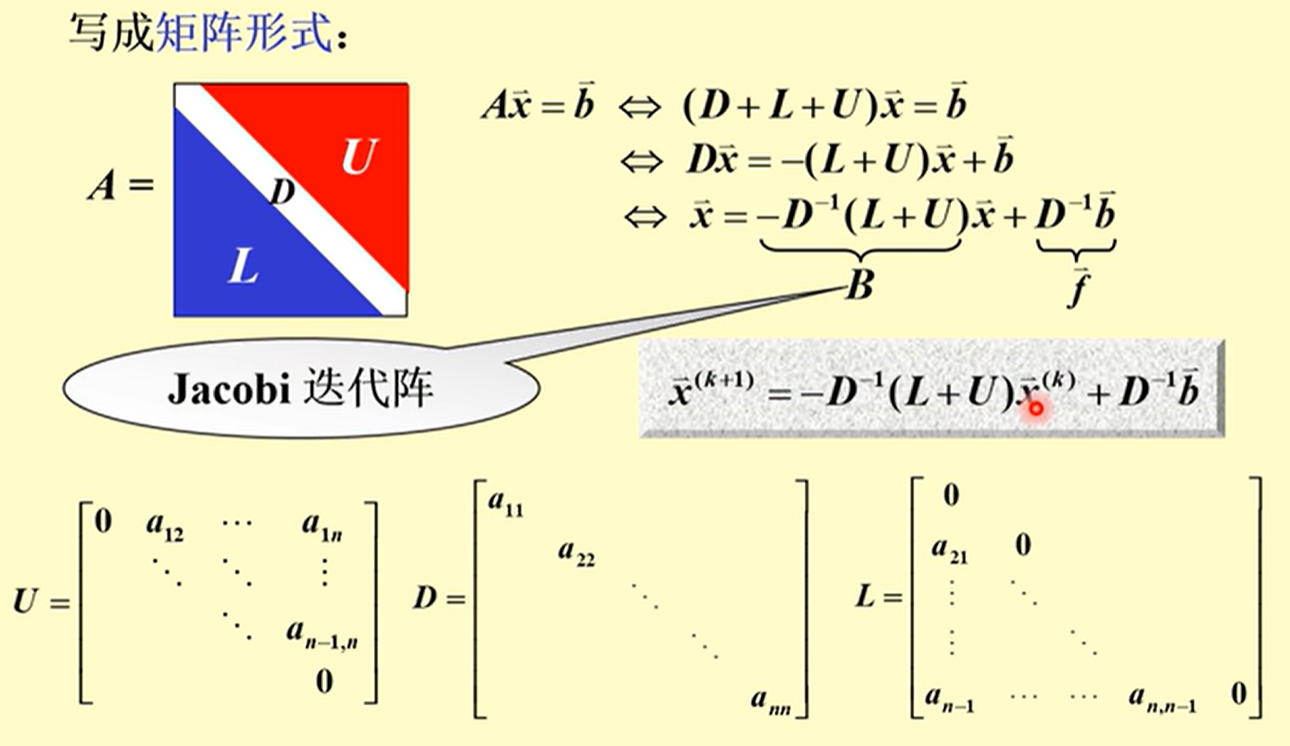
这种方法进行分解后,就相当于例子中,把每个变量放一边的方法
Gauss-Seidel 迭代法

在 jacobi 迭代法的基础上进一步思考:在计算时,的值都已经计算出,可以带入计算的公式中
Gauss-Seidel 分量形式

Gauss-Seidel 矩阵形式

注:两种方法都存在收敛性问题
迭代法的收敛性
收敛条件:

从上述推导可以发现,为零矩阵,则最后的误差为 0,说明迭代法收敛;

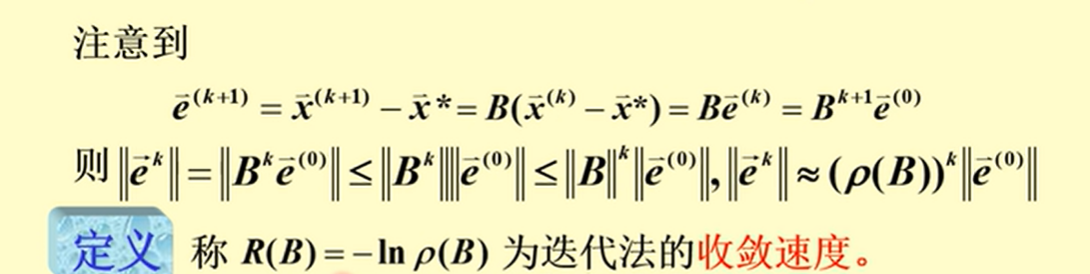
而 收敛的充要条件就是 的谱半径 ,==且 越小,则迭代收敛越快==
四个充分条件
- 由定理可知,任意一个范数,那么只要证明,即可证明收敛

- 若为严格对角占优阵,则解的 Jacobi 和 Gauss-Seidel 迭代均收敛

- 若为弱严格对角占优阵,且为不可约矩阵,则解的 Jacobi 和 Gauss-Seidel 迭代均收敛
- 若正定,则解的 Jacobi 和 Gauss-Seidel 迭代均收敛
松弛迭代法
复习 6 章 & 6.6.3 松弛迭代法 SOR_哔哩哔哩_bilibili
基本思路
换个角度看 Gauss-Seidel 迭代法:将其看作增量形式,目标就是要求出增量

矩阵形式
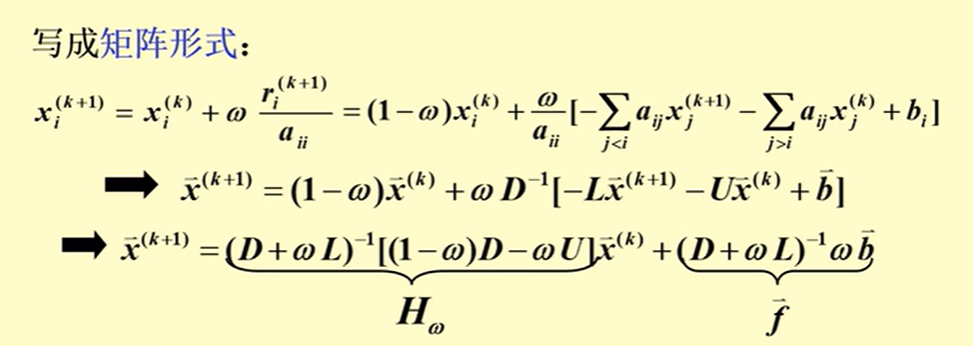
收敛性判断
对于这个形式,判断其收敛性:
- 使用充分必要条件 计算过于复杂,很难计算
- 使用 Kahan 必要条件

- 使用其他充分条件

Chapter 7. 非线性方程组和方程组的数值解法
6.6.3 & 7 非线性方程组的解法_哔哩哔哩_bilibili

次数越高,其方程的解析解就越难以表示,5 次以上更是没有解析解,因此我们需要通过求解近似值的方式,不断逼近零点
二分法
基本思想
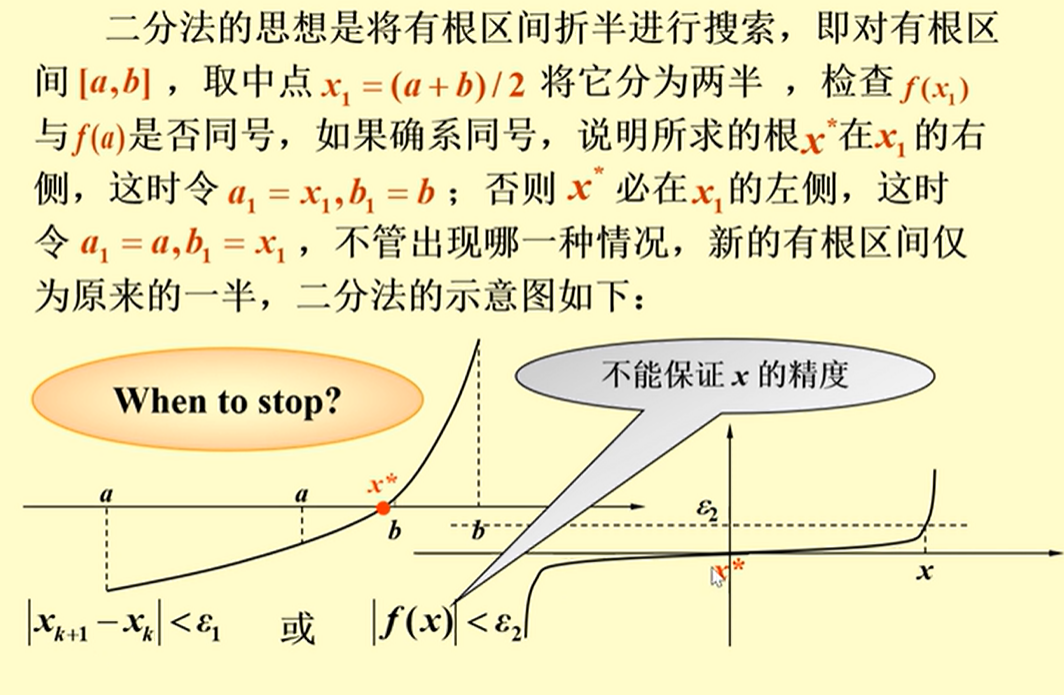
对有根区间进行折半查找…
优点:算法简单,对的要求不高,只要保证连续即可
缺点:不能够保证 x 的精度,无法求重根和复根
误差分析

一个例子
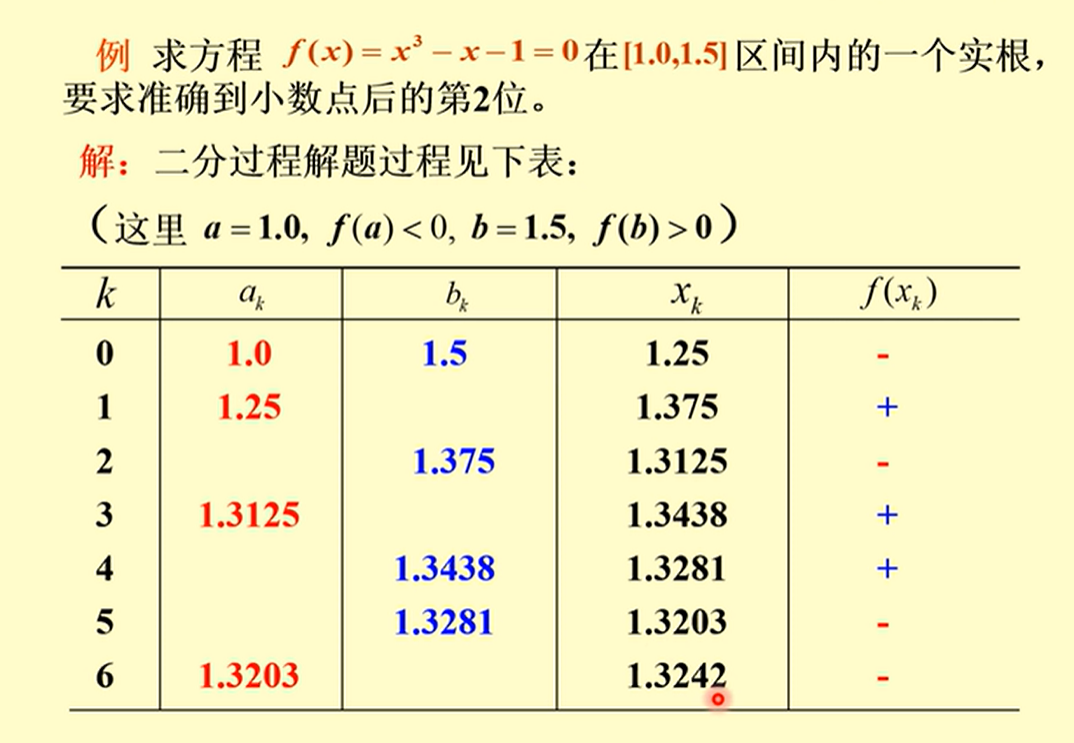
如果相邻两个点的变化值,不到其最后一位精度,则说明精度是够的
简单迭代法
基本思想
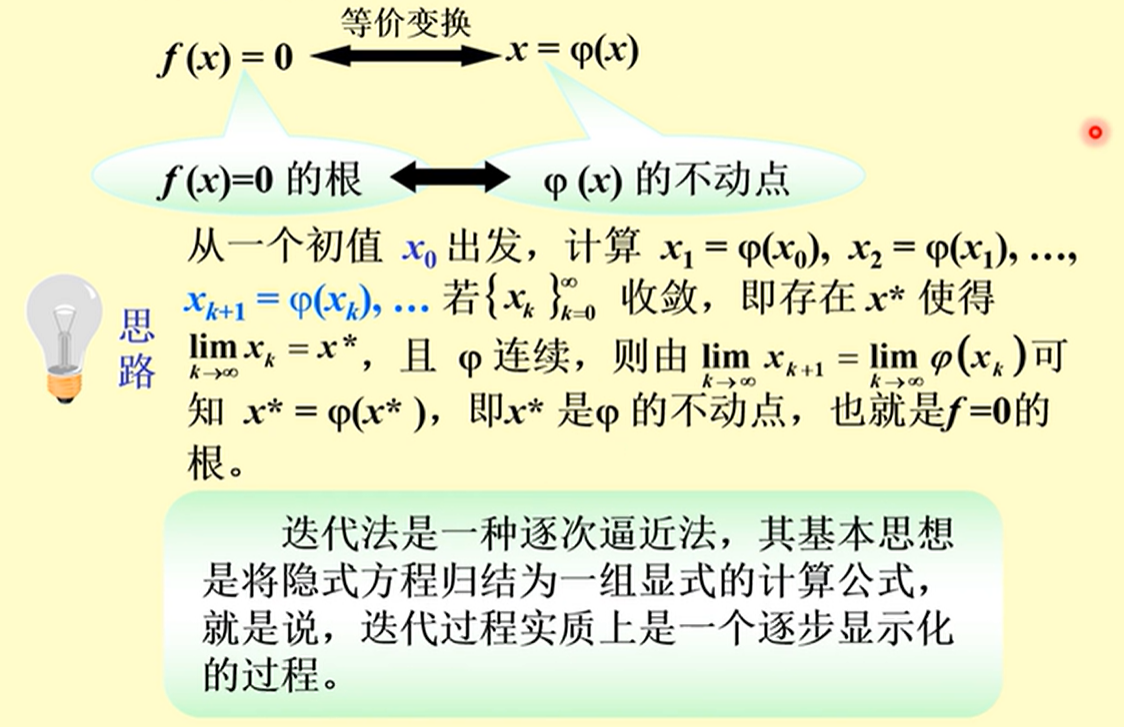
如果每次迭代,使得能够收敛,就说明是的不动点,也就是的根
但是不能保证每个迭代函数都一定是收敛的!!!
一个例子
同一个方程有不同的等价迭代函数:

但是计算后有的收敛,有的不收敛:

在这个例子中,有以下问题需要进行详细讨论:
- 如何选取合适的迭代函数?
- 迭代函数应该满足什么条件,序列收敛?
- 怎样加速序列的收敛?
迭代收敛的过程
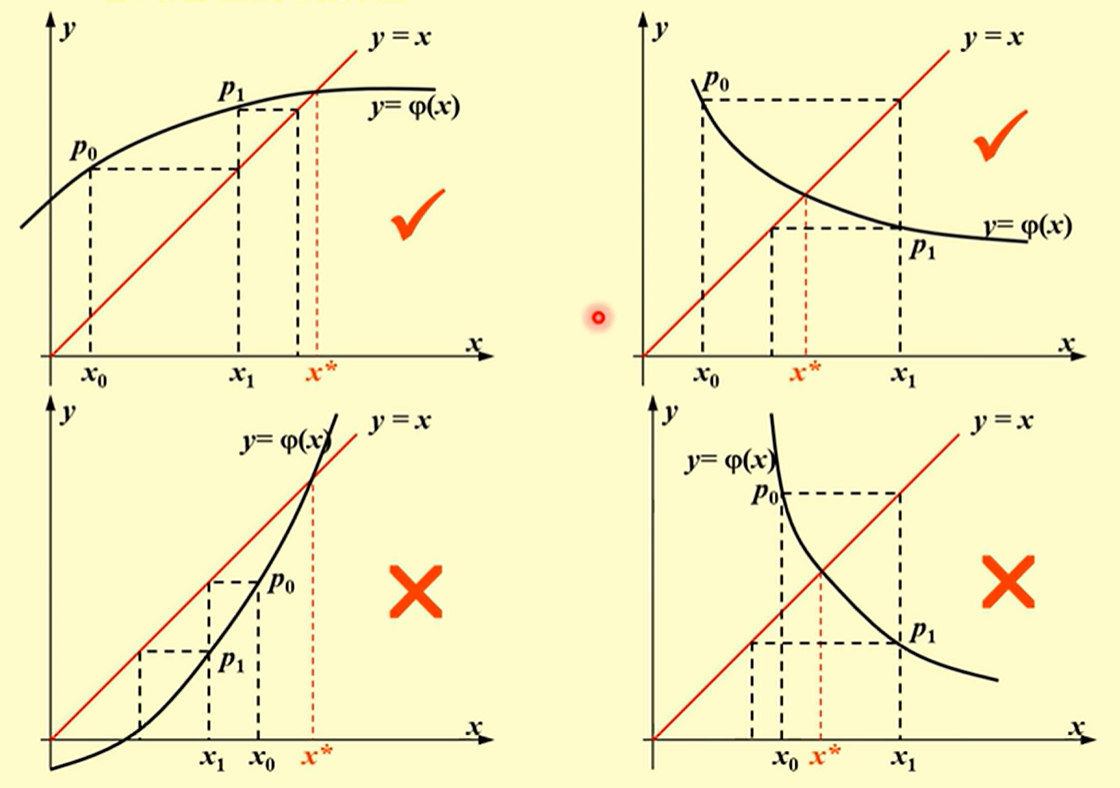
定理


p 阶收敛的迭代法

迭代加速
迭代收敛速度

Aitken 算法
基本原理

可以加速收敛的原因:
- 实际上求出两次迭代值,然后通过加权的方式得到改进值,相比原式来说更加稳定
- 原函数往往比较复杂,导致往往也是一个复杂函数,通过这种方式可以少计算,从而达到加速的效果
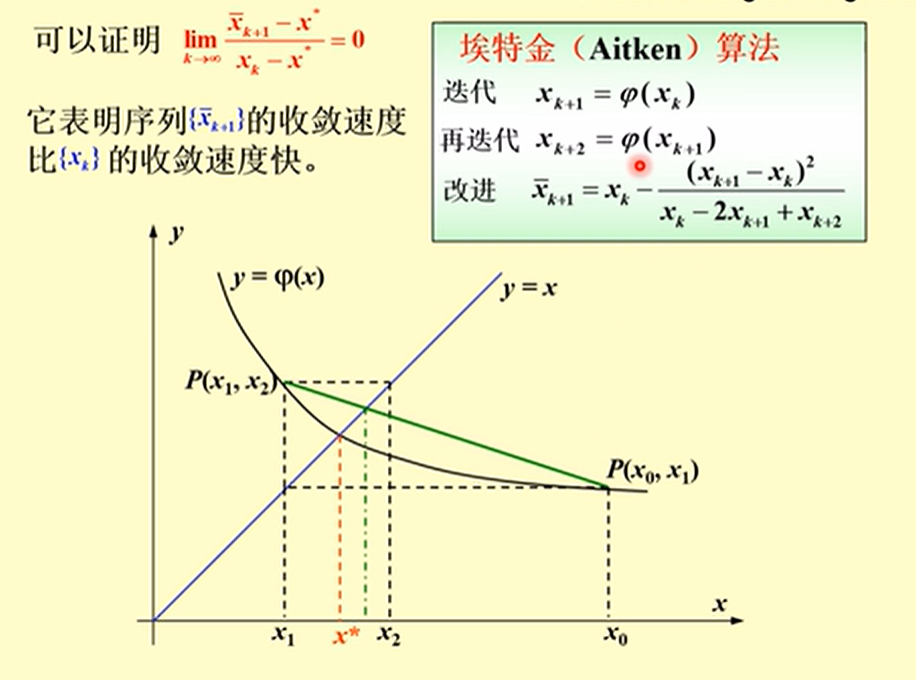
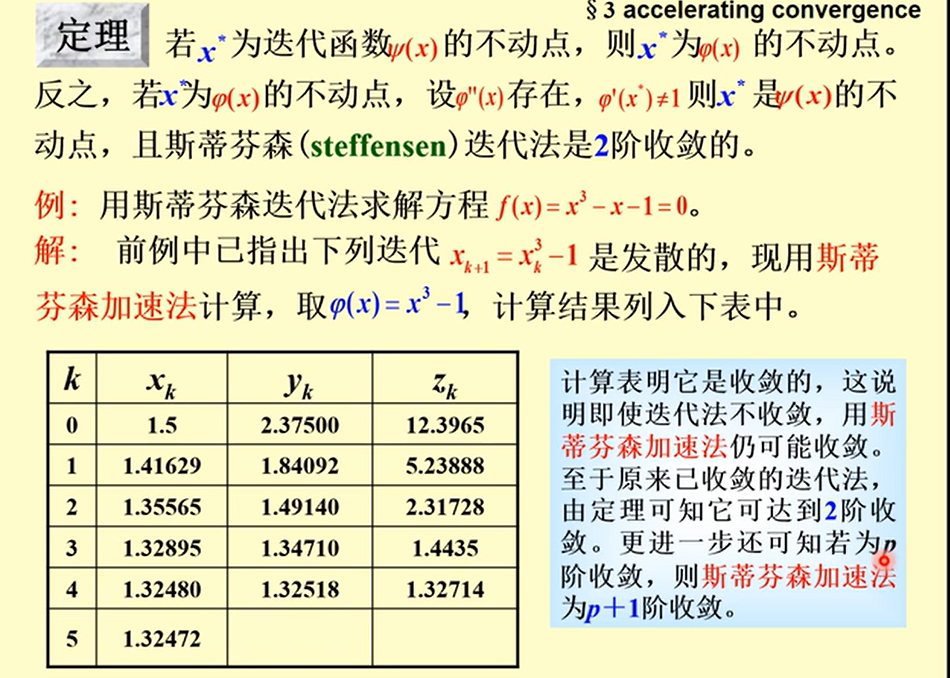
Steffensen 迭代法

收敛效果
Newton 法
基本思想
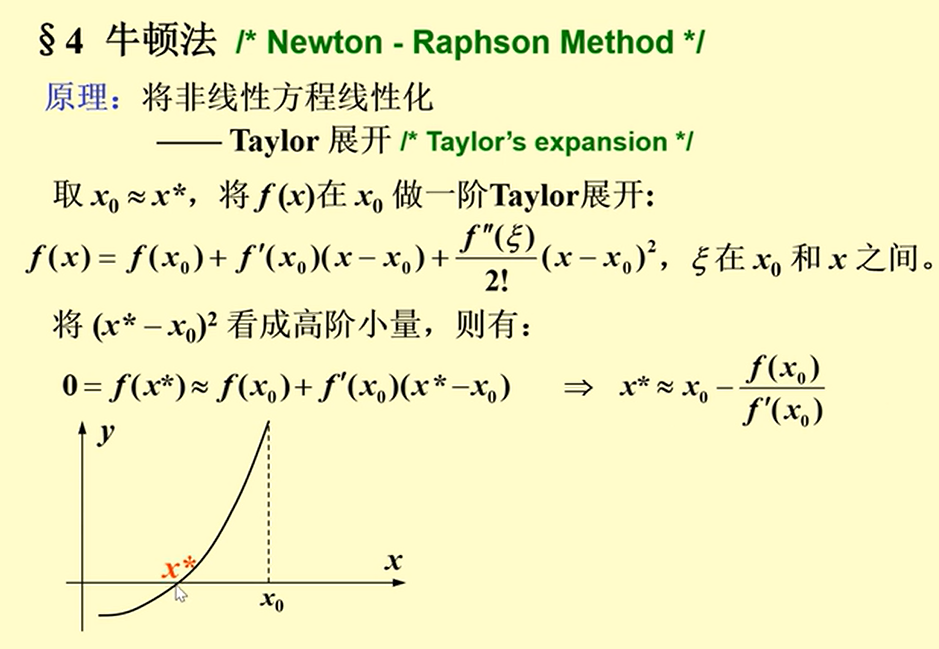
基本思想就是将非线性方程线性化,原函数做一阶 Taylor 展开,并且将二阶看作高阶无穷小量,就可以得到一个稳定的迭代公式

Newton 法的改进
Newton 下山法
基本思想

选取一个作为下山因子,一般下山因子从 1 开始…不断减半,使得能够保证收敛
弦截法